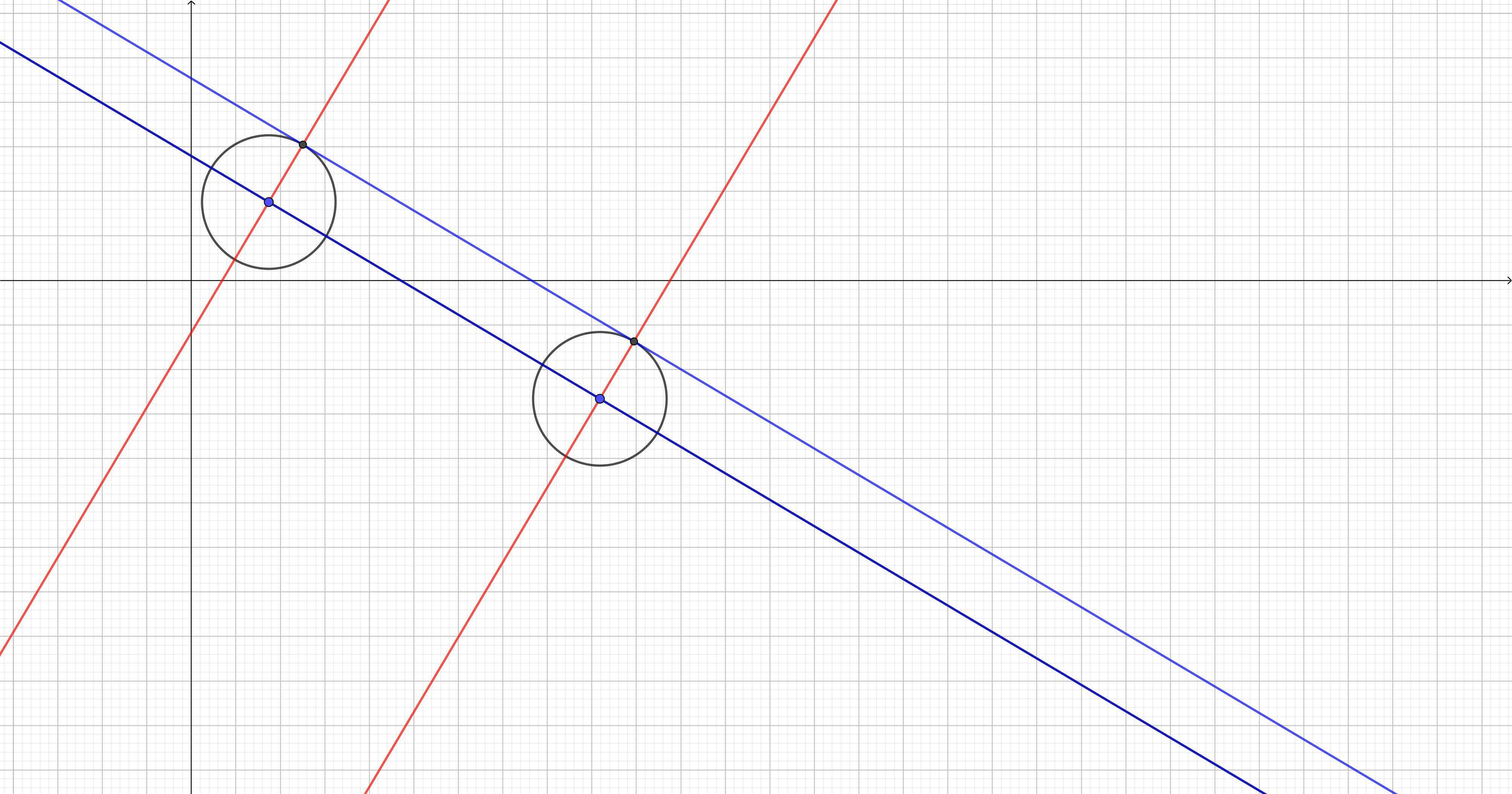
To construct a #ParallelLine to a given line (in blue) in 2D #EuclideanSpace, all you need to do is pick two #points and draw #circles centred at those points of a specified #radius. Draw a #perpendicular to the line at each point (in red) and then draw a new line passing through the intersection of the perpendicular with the circles and there is the line parallel to the original one. Here is the process shown in #Geogebra.

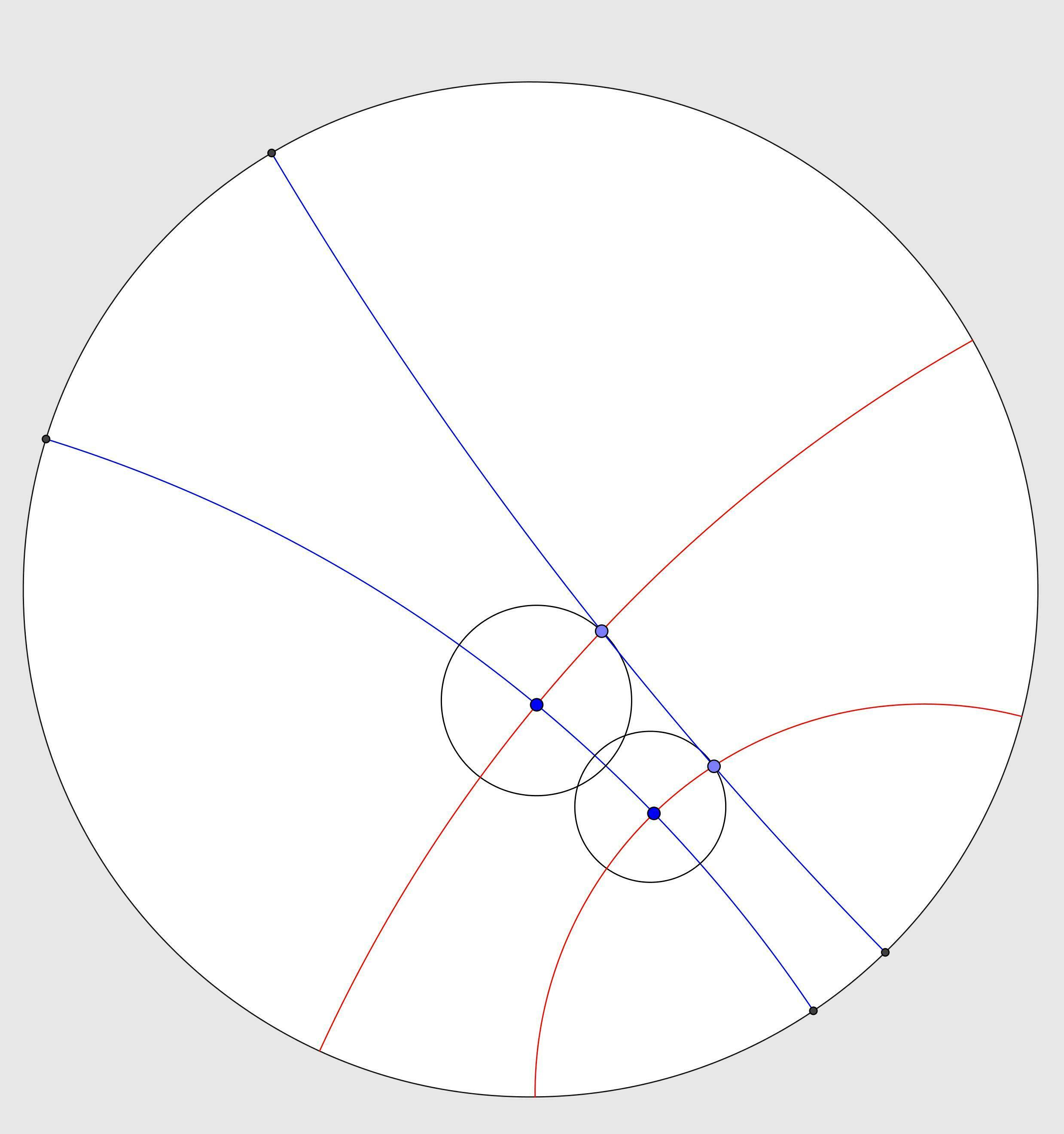
Using this #software, you can also explore #non-Euclidean space and here is the same action in #HyperbolicSpace (here in a #PoincaréDisc). #StraightLines are replaced by #GeodesicLines which look like #CircularArcs which intersect the #disc at #RightAngles. Circles are transformed to circles but their hyperbolic centres are not at the centre of their Euclidean centres. The boundary is analogous to infinity.

Repeating the construction for Euclidean space, you can see that the parallel lines diverge.

#Mathematics #Geometry #NonEucldeanGeometry #EuclideanGeometry #FreeSoftware