
0.001 100e6
.01 19.1e6
0.1 3.8e6
0.5 0.402e6
Gini-Koeffizient 1/(2 * k -1 )
k=1.4082 : G = 0.55
k=1.15 : G = 0.77
Neulich bei DIASPORA entdeckt: xxx
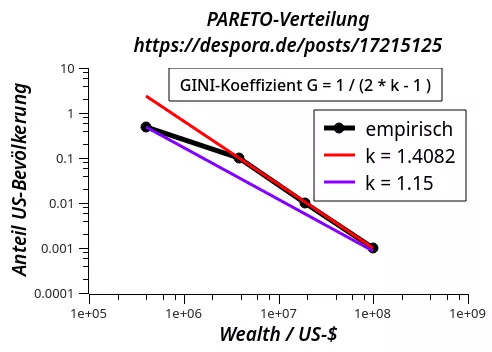
In der Ausgangsgraphik mit den Daten geht es um die Vermögensverteilung in US-Amerika.
Die Vermögensverteilung gehorcht oft einer PARETO-Verteilung:
https://de.wikipedia.org/wiki/Pareto-Verteilung
In einer graphischen Darstellung der Daten ist zu ersehen, daß ab den Einkommen der oberen Mittelschicht die Vermögensverteilung in einer doppeltlogarithmischen Darstellung auf einer Geraden liegen, wie es bei einer PARETO-Verteilung zu erwarten ist.
Im Bereich der kleineren Vermögen scheint es dagegen eine quasi demokratische Vermögensverteilung zu geben, die Kurve im Diagramm flacht ab.
Aus den Potenzkoeffizienten k kann der GINI-Koeffizient berechnet werden:
https://digitalscholarship.unlv.edu/cgi/viewcontent.cgi?article=4277&context=rtds
Mit den k-Werten aus dem PARETO-Diagramm können die folgenden Gini-Koeffizienten berechnet werden:
k = 1.4082 -> G = 0.55
k = 1.15 -> G = 0.77
In der WIKIPEDIA-Seite über die GINI-Koeffizienten findet sich eine Übersicht über diese Koeffizienten weltweit. Demnach haben die USA einen Gini-Koeffizienten von 0.4 - 0.45. Weltweit gibt es nur wenigige Länder - v.a. Südafrika und Brasilien - in denen der Gini-Koeffizient Werte von 0.55 und mehr erreicht.
Insgesamt scheinen die Ausgangsdaten nicht realistisch für die USA zu sein.
Mit zusätzlichem Datenpunkt_
k = 1.4082 -> G = 0.55
k = 1.18 -> G = 0.74


