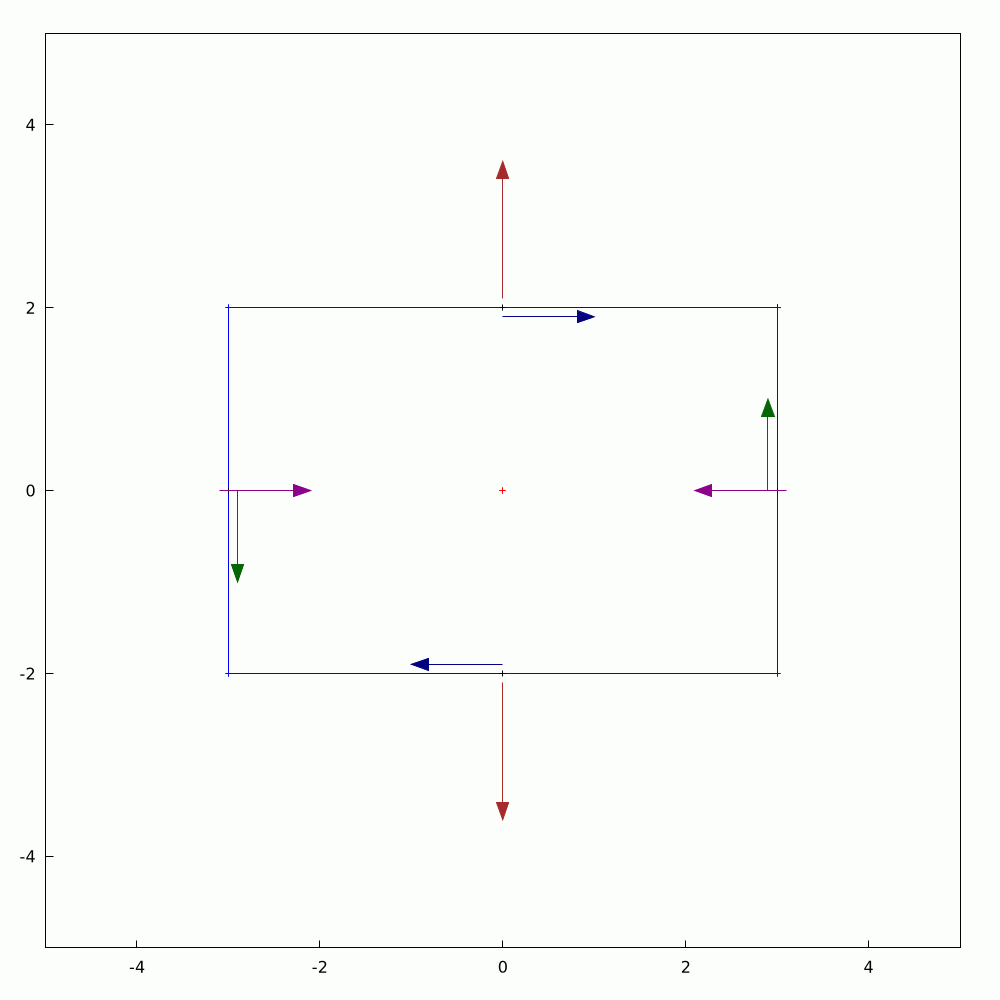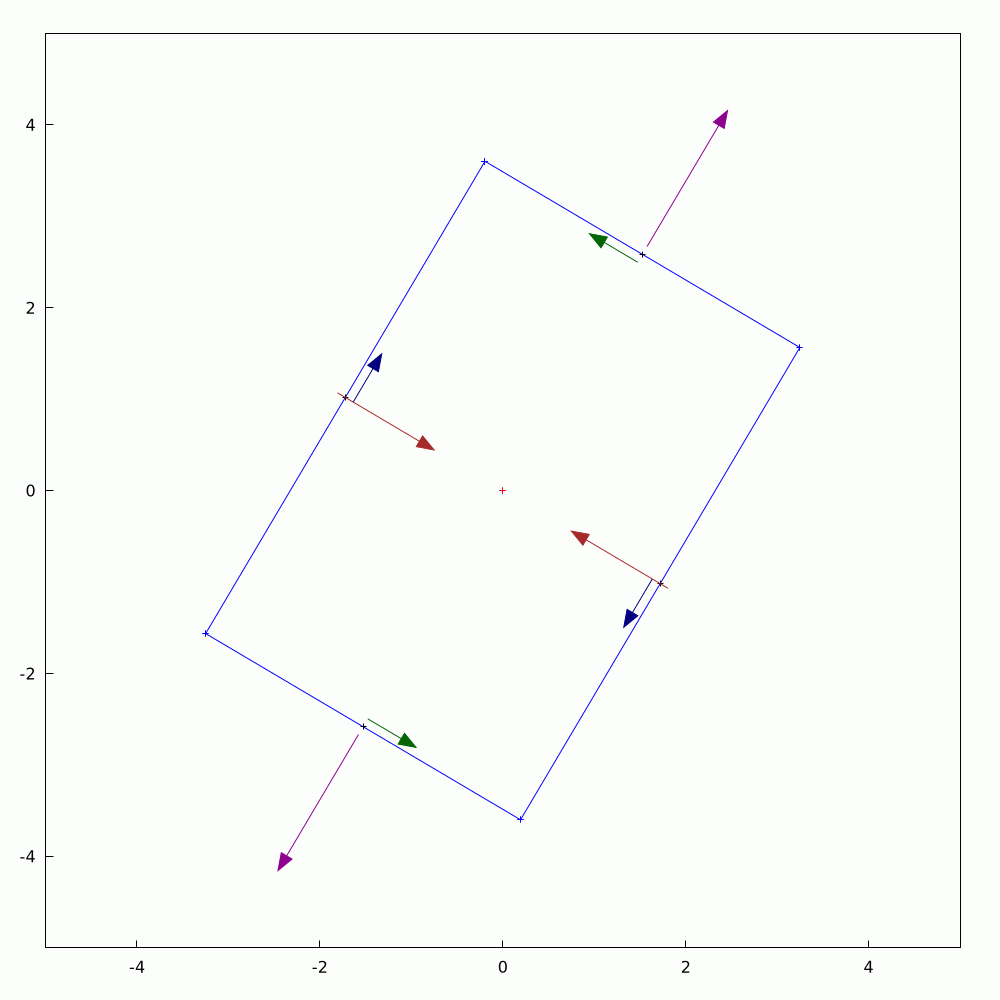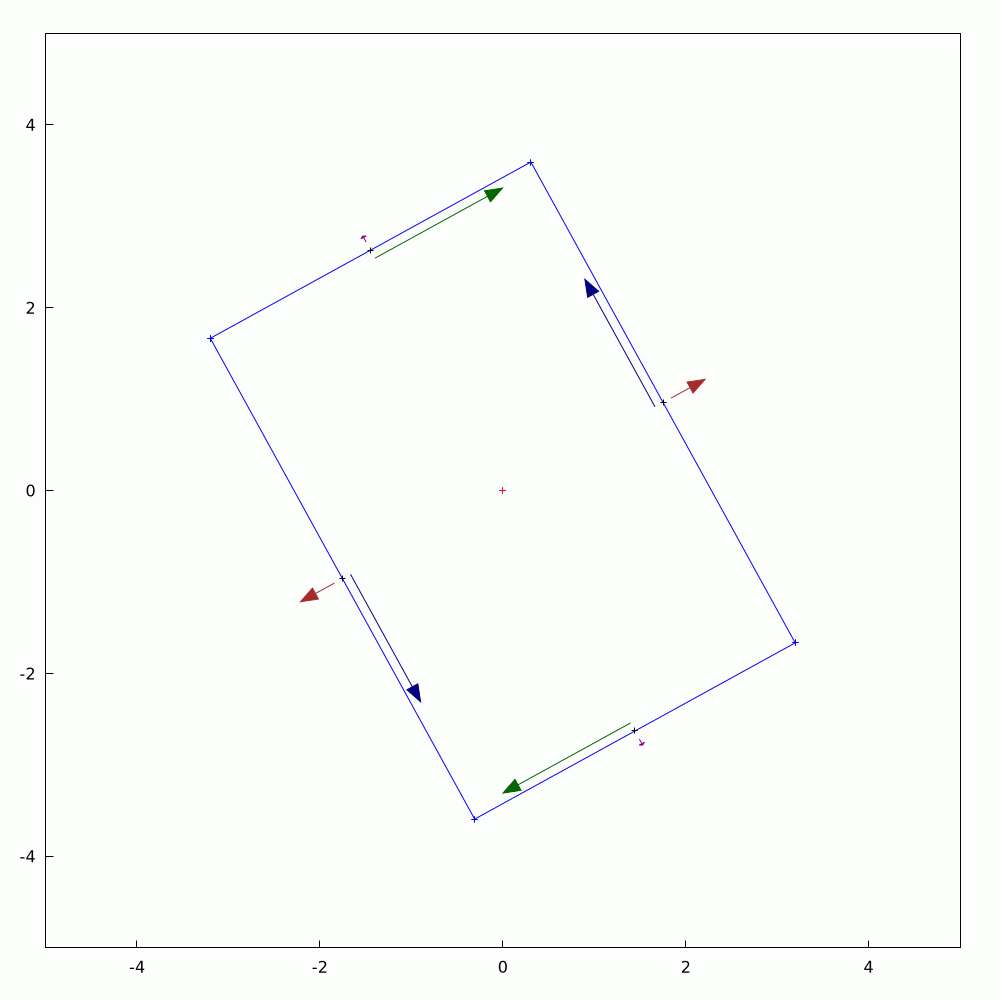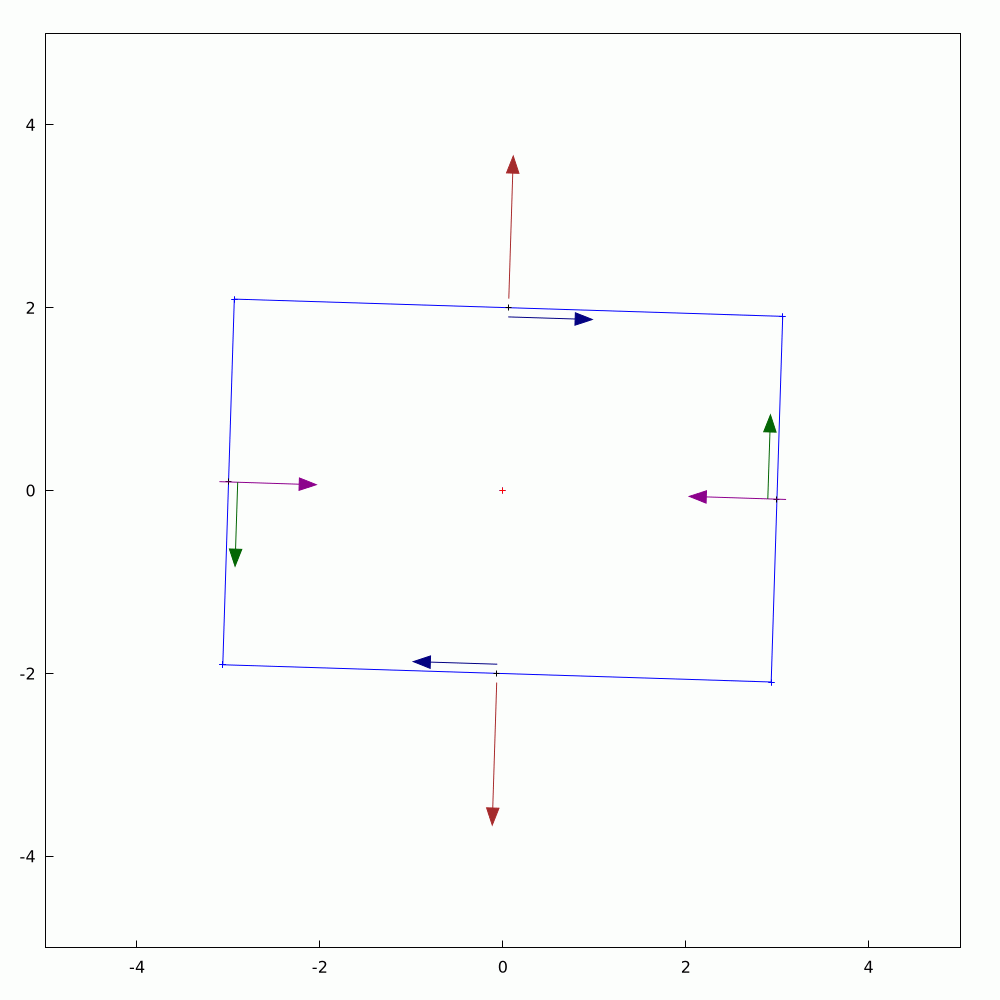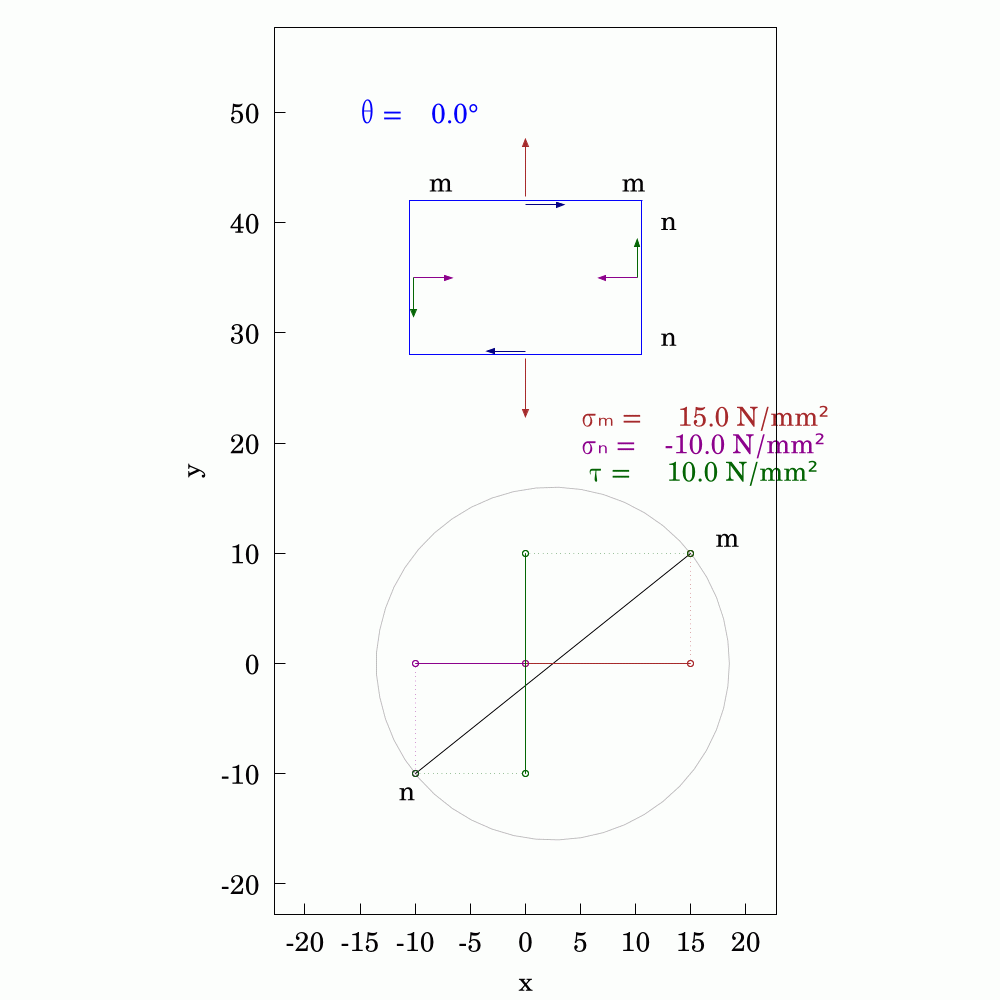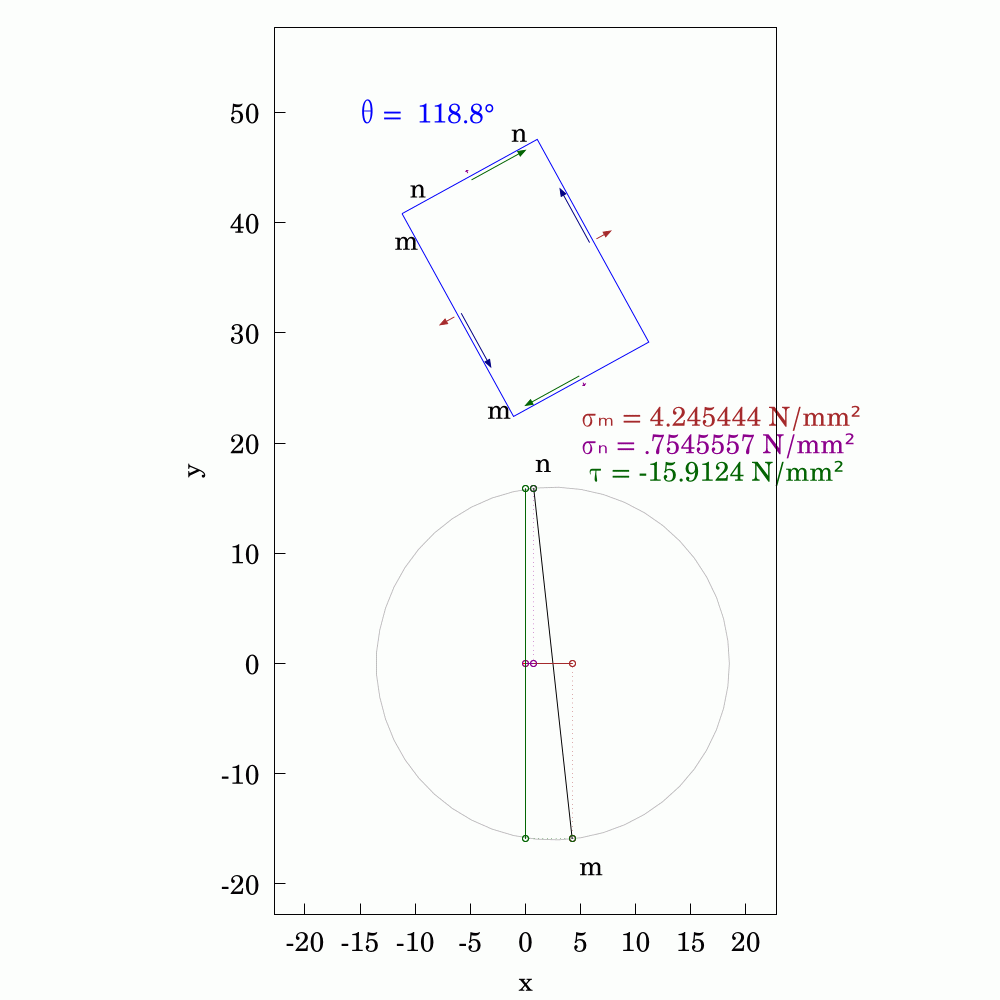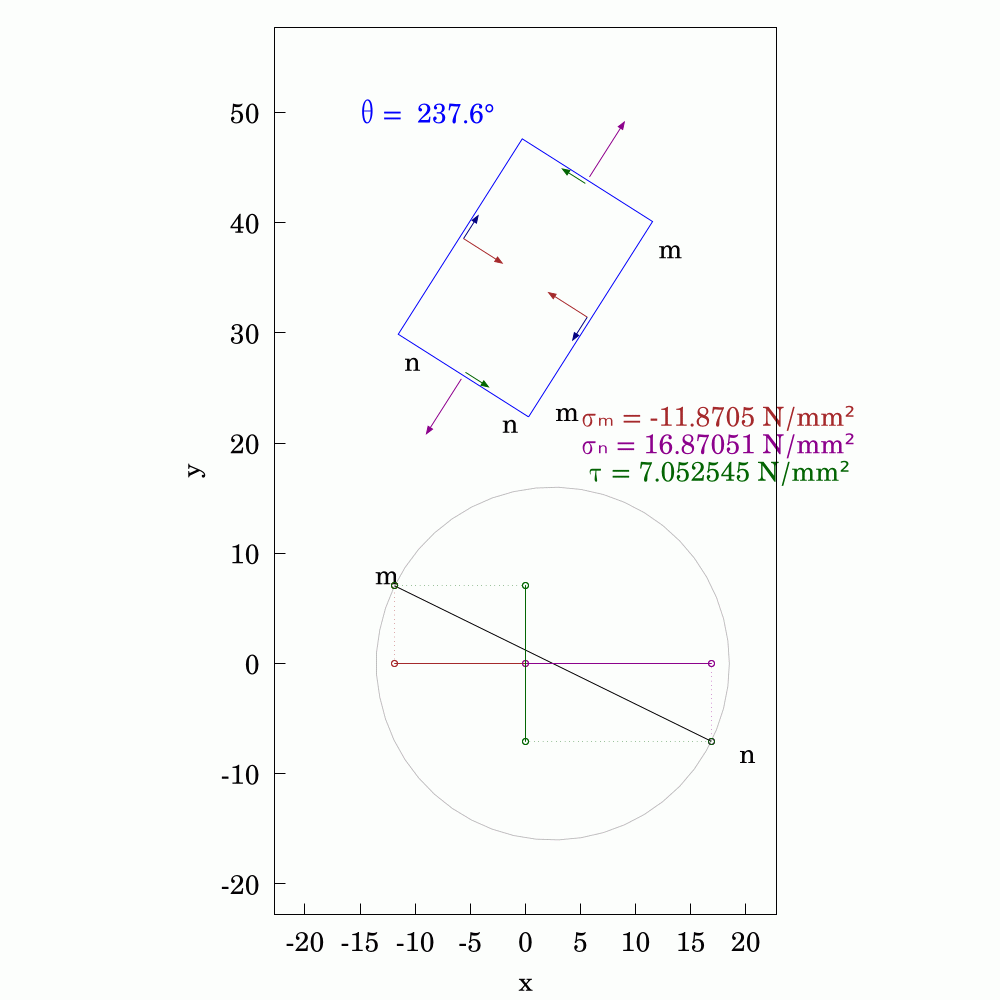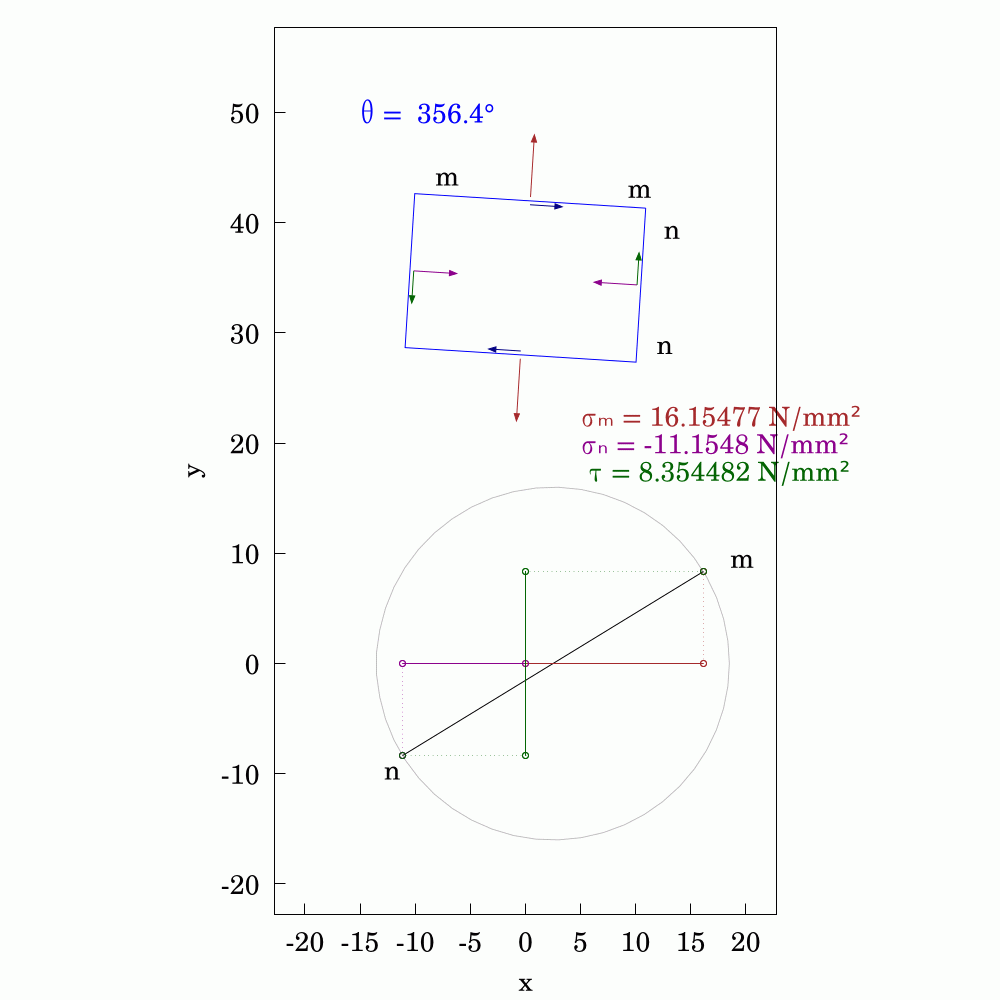
In #SolidMechanics, #stress has some counter-intuitive properties, particularly when you rotate the coordinate system. The values of normal and shear stress transform according to the rules of #second-order #tensors, which is a step above #vectors (first-order tensors). To avoid always having to use #matrix #algebra to find the components, #engineers and #mathematicians have long used the Mohr's circle to evaluate them. This is a very handy tool and allows you to find the new values by using circular geometry instead.

Here, I've used #WxMaxima to create this #animation.

#Mechanics #Mathematics #Engineering #MohrsCircle #FreeSoftware

In the #2D #elasticity, #equilibrium of #stresses can be represented on an infinitesimal rectangular element with components of both #DirectStress and #ShearStress generally acting on all four edges. If you were to rotate the rectangle, the stresses change in a precisely orchestrated fashion. In the orientation where the shear stress components vanish, we get what are called #PrincipalStresses and they and their directions can be ascertained precisely through #eigenvalue analysis. This little graphical demonstration shows one example of such a state. The #AnimatedGif was produced a routine written in #WxMaxima.

#Mathematics #TheoryOfElasticity #Mechanics #SolidMechanics #Engineering #MyWork #CCBYSA #WorkInProgress