Aus einer alten Fangfrage um Schöpfungsgeschichten ergeben sich interessante Erkenntnisse – und nebenher ein Verfahren, um Gleichungen zu lösen.#Mathematik #Algebra #Gleichungen #Logik #Rätsel
Mathematik mit Wasser und Wein
#algebra
Der Mörder Christopher Havens hat ein jahrzehntealtes Mathematikproblem gelöst. Mit dem Prison Mathematics Project hofft er auch andere Häftlinge für das Fach zu begeistern.#Fabelhaftemathematik #Mathematik #Mord #Kettenbruch #Algebra #Zahlentheorie
Erst Mord, dann Mathe
Anfang 2024 wurde eine neue Gleichung zur Berechnung von Pi vorgestellt. Zwei indische Physiker stießen darauf, als sie versuchten, dem Konzept einer Weltformel näherzukommen.#FabelhafteMathematik #Pi #Kreiszahl #Stringtheorie #Madhava #Algebra #Weltformel #Mathematik
Stringtheoretiker finden eine neue Formel für Pi
Die Kür in der Mathematik besteht darin, Brücken zu schlagen. Nun haben Forscher einen Zusammenhang zwischen Elektromagnetismus, Geometrie und Zahlentheorie entdeckt.#Langlands-Programm #Galois #Galoisgruppe #Algebra #Zahlentheorie #Geometrie #Fermat #Riemann #RiemannscheVermutung #Gruppentheorie #Symmetrie #Wiles #Mathematik #Physik
Ungeahnte Verbindung zwischen Physik und Zahlentheorie
Die Mathematik löst Probleme. Doch manchmal ist es wichtiger, vorab zu prüfen, ob es überhaupt eine Lösung gibt.#SatzvonKronecker-Capelli #Freistetter #FreistettersFormelwelt #Mathematik #Algebra #Gauß
Freistetters Formelwelt: Ein Theorem für Faule
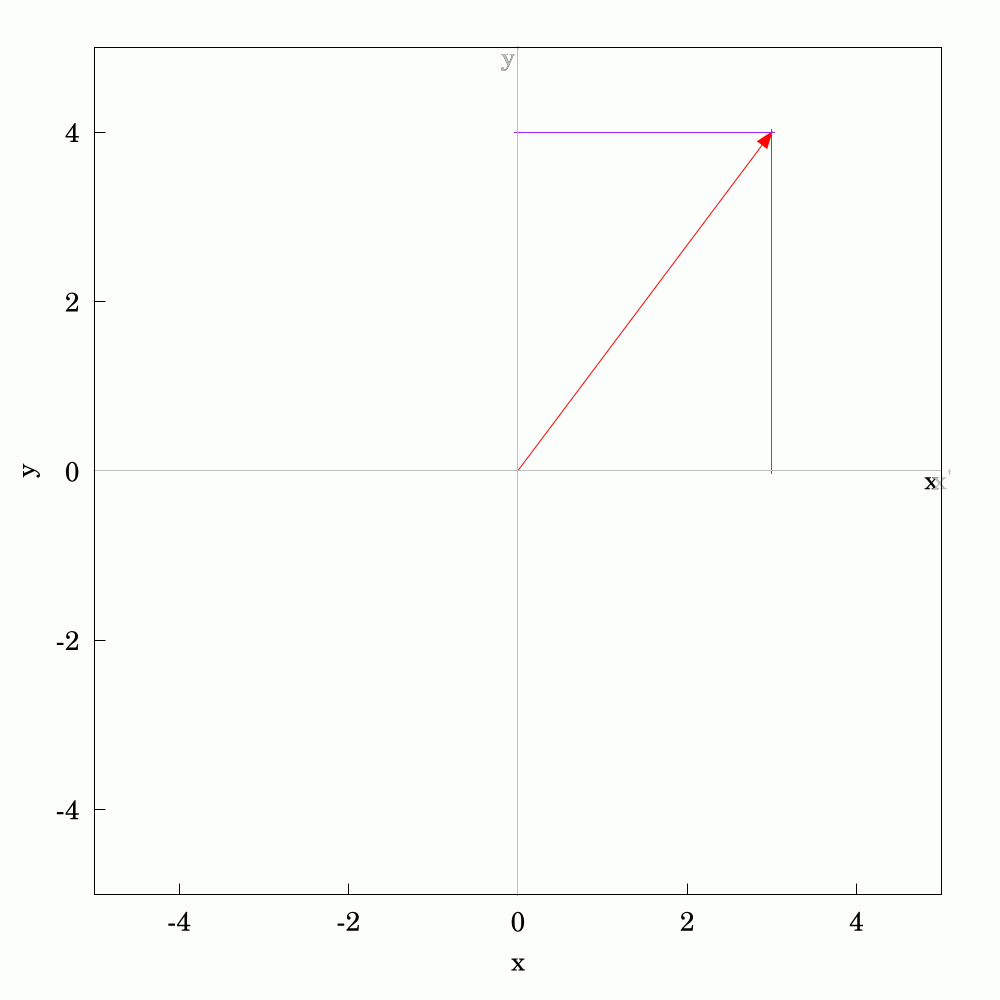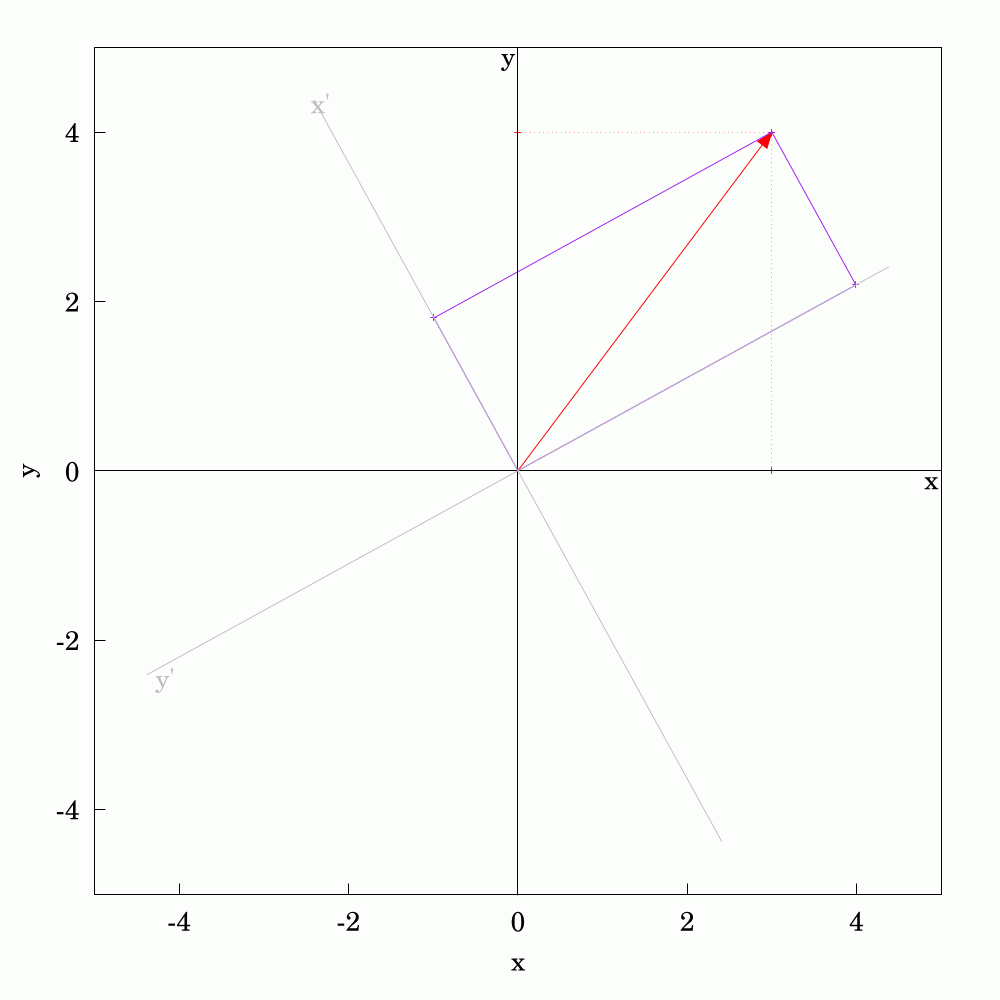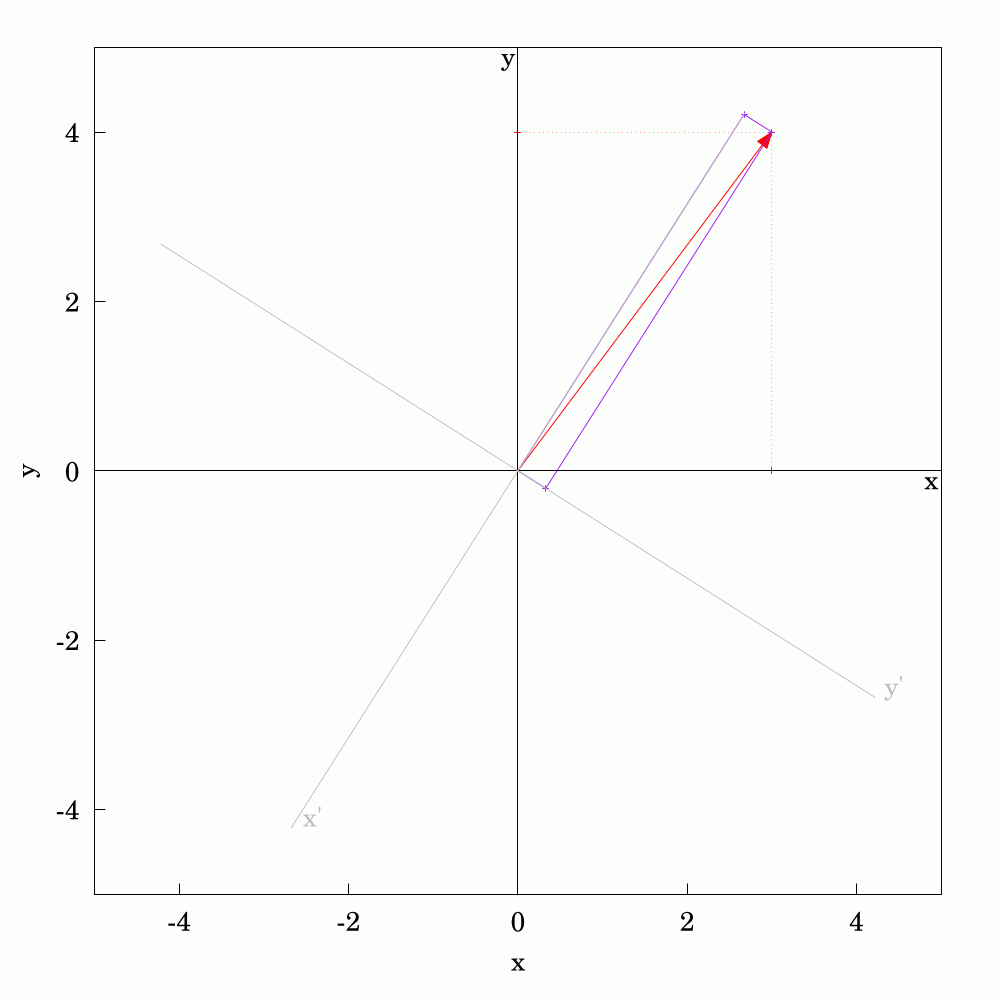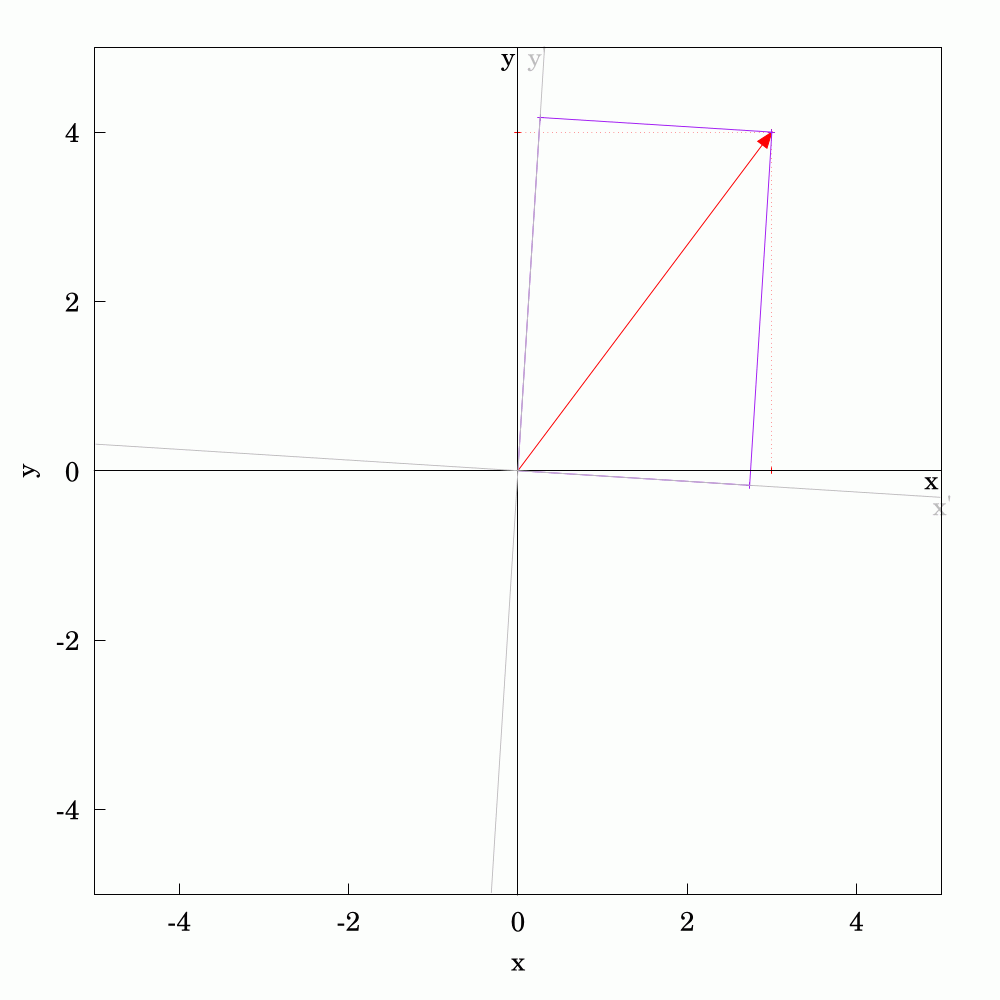
It's straightforward to calculate the #components of a #2D #vector given that you have a pre-defined set of #axes. Often, we talk about #cartesian #coordinates. If the vector changes, whether in #magnitude or #direction, we can calculate the updated components too. The converse question is what if the the vector is held constant and you change or #rotate the axes? The components in the new coordinate system can be found with a little bit of #trigonometry and #algebra. As vectors are #first-order #tensors, they are much simpler to calculate than quantities like stress for which I've also made an animation for if you search for the hashtag #tensors.
In this animation, you can see the components changing as the axes go through a full rotation.
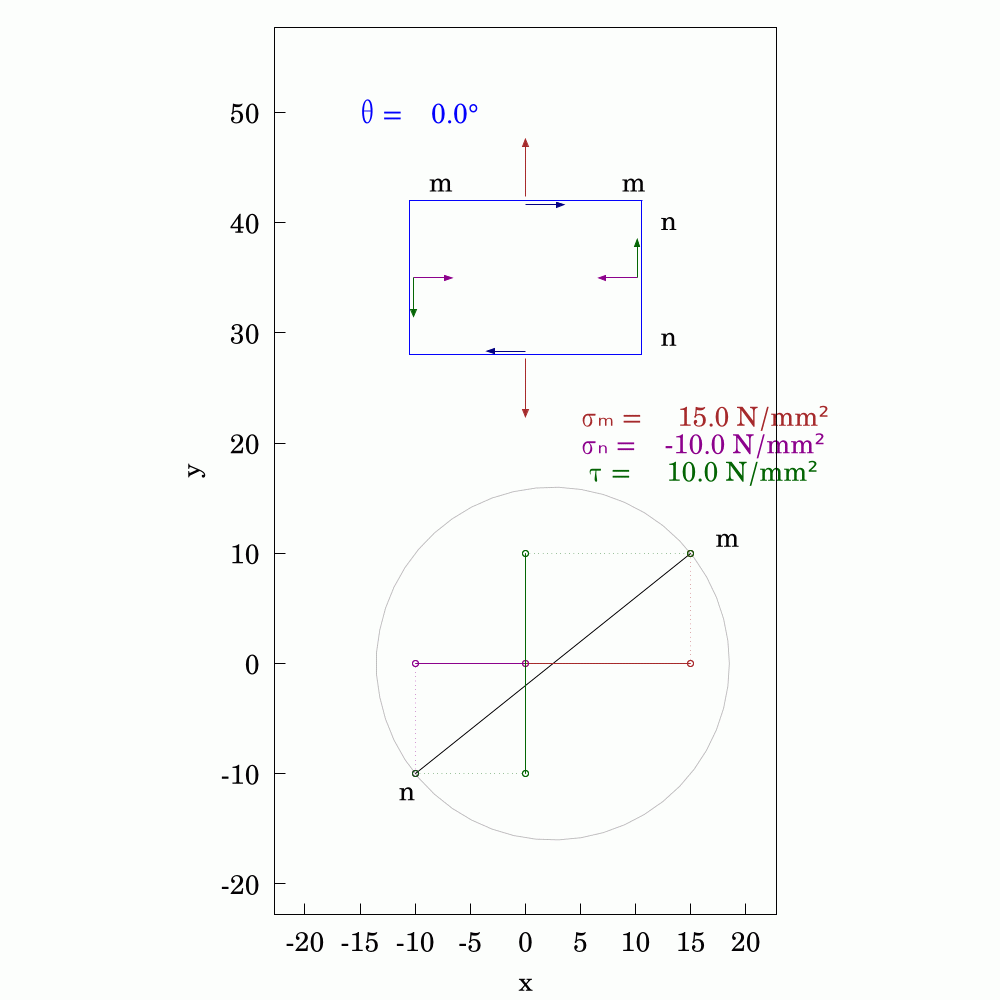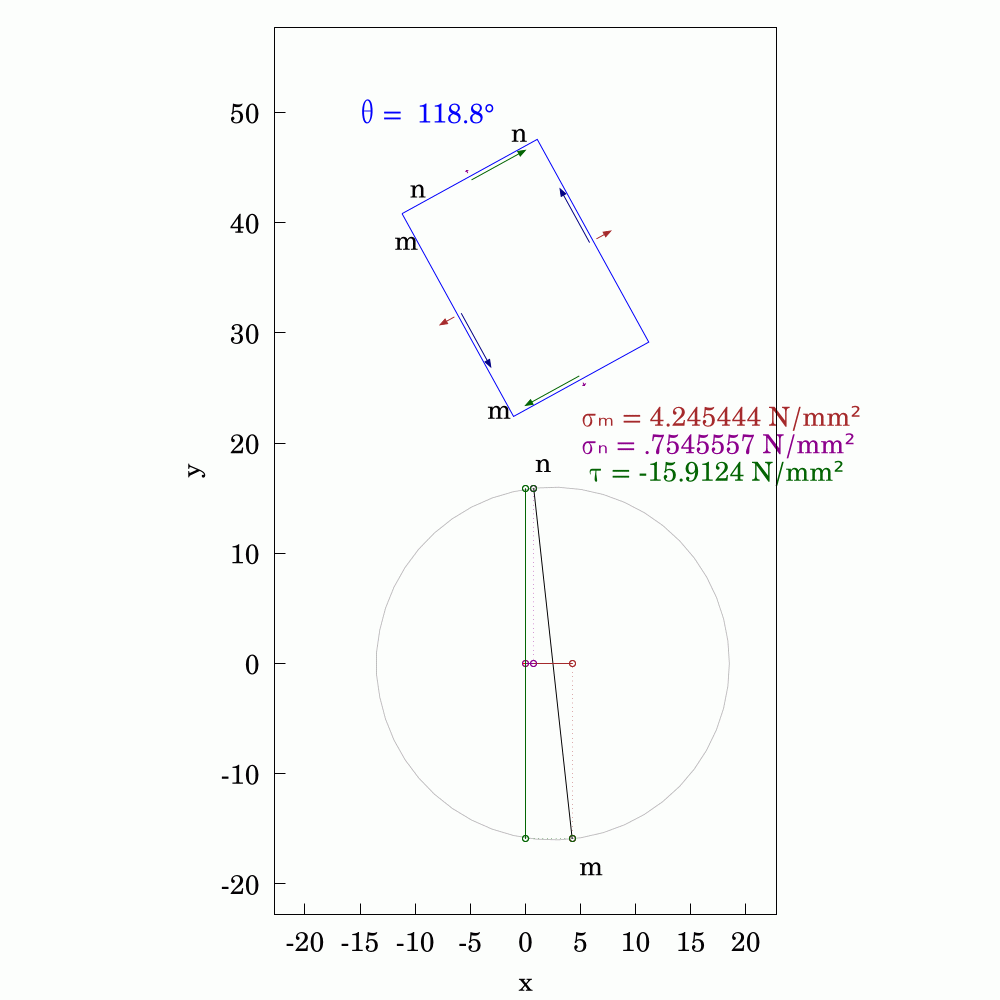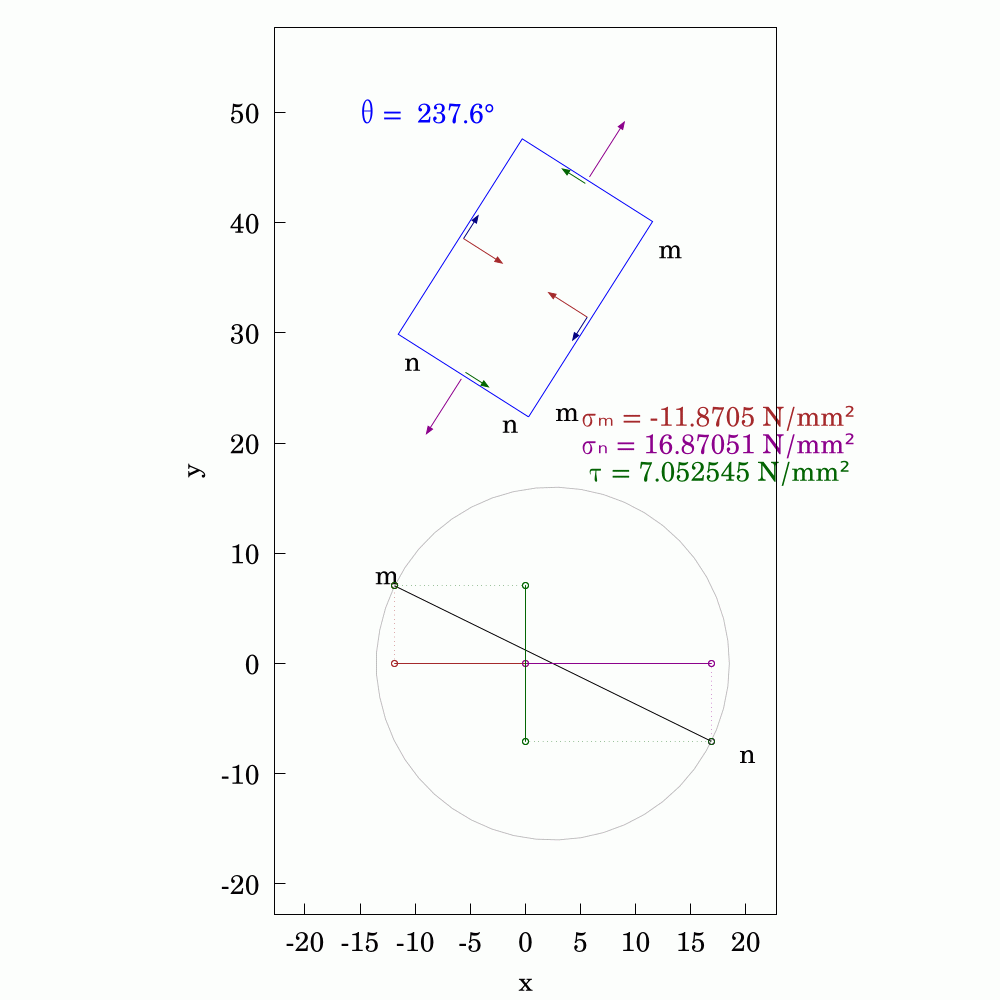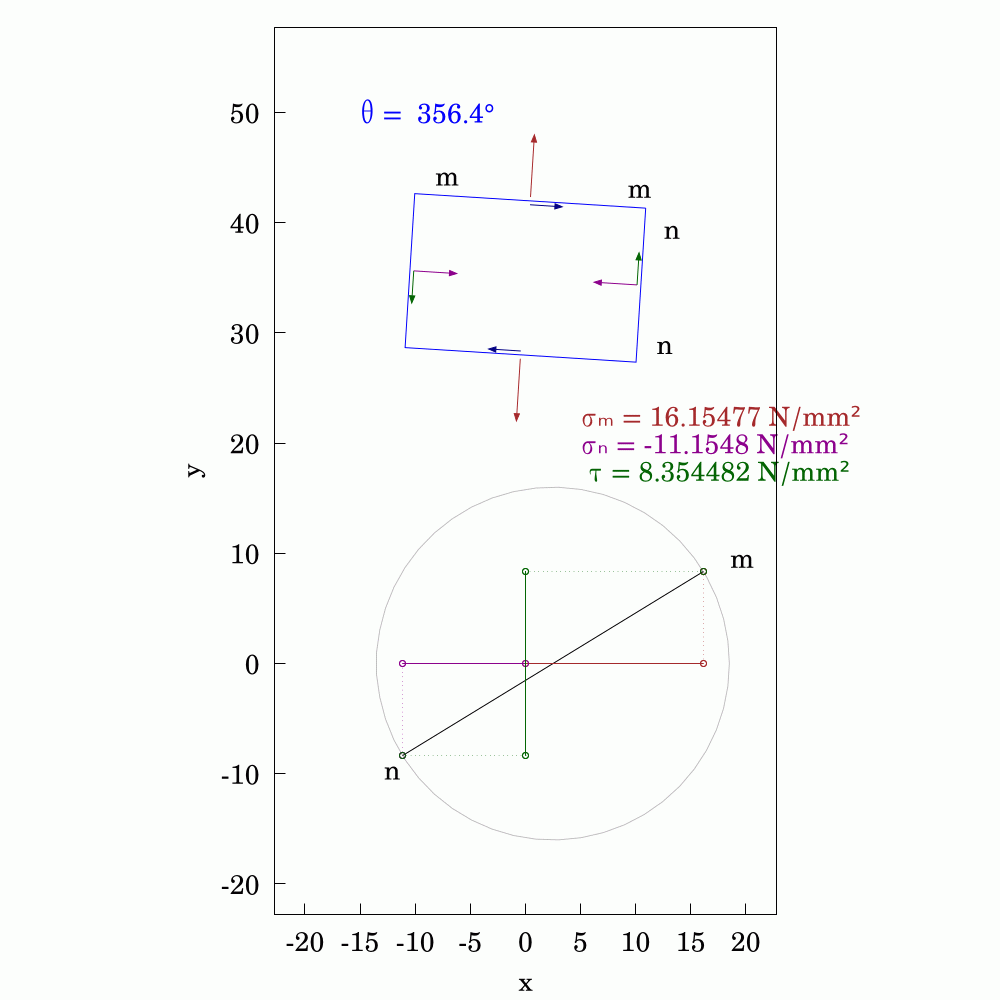
In #SolidMechanics, #stress has some counter-intuitive properties, particularly when you rotate the coordinate system. The values of normal and shear stress transform according to the rules of #second-order #tensors, which is a step above #vectors (first-order tensors). To avoid always having to use #matrix #algebra to find the components, #engineers and #mathematicians have long used the Mohr's circle to evaluate them. This is a very handy tool and allows you to find the new values by using circular geometry instead.
Here, I've used #WxMaxima to create this #animation.
#Mechanics #Mathematics #Engineering #MohrsCircle #FreeSoftware
● NEWS ● #DemocracyNow ☞ Remembering #CivilRights Icon Bob Moses: Organized SNCC, Miss. Freedom Summer & #Algebra Project https://www.democracynow.org/2021/7/26/rip_civil_rights_leader_bob_moses
