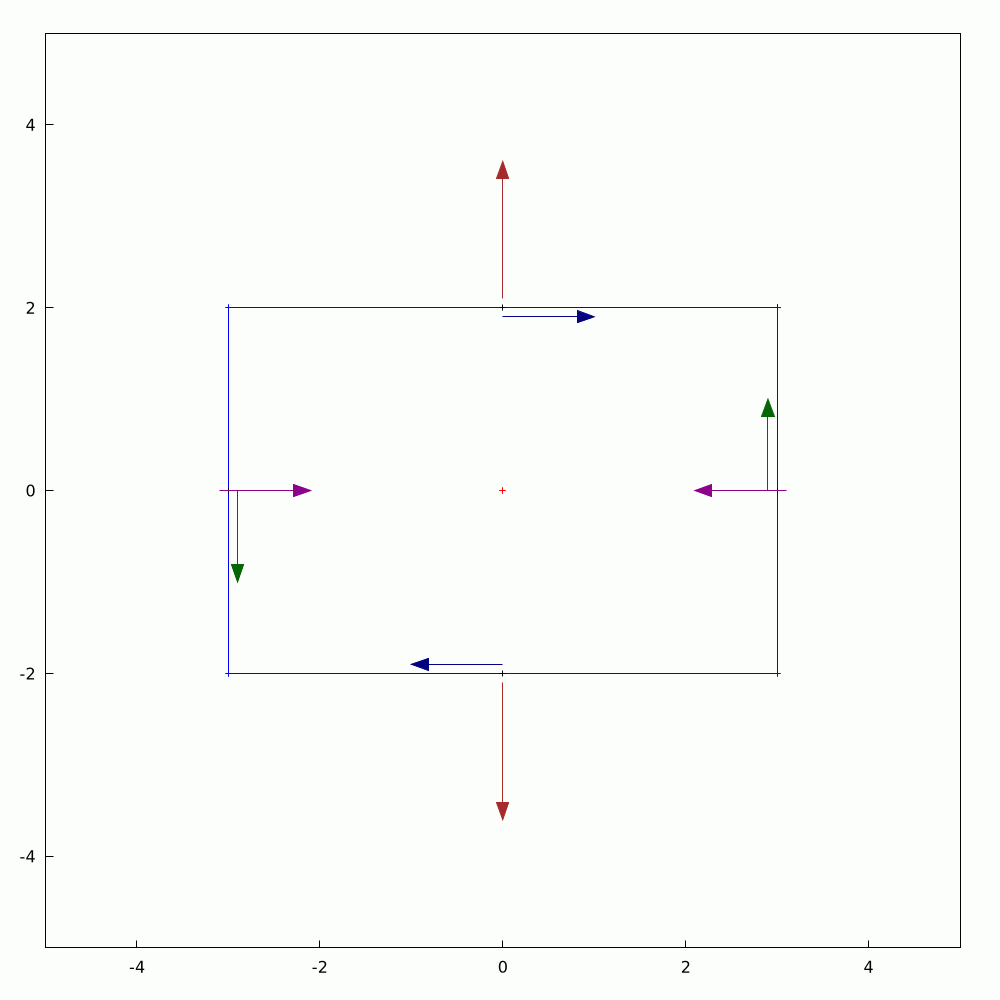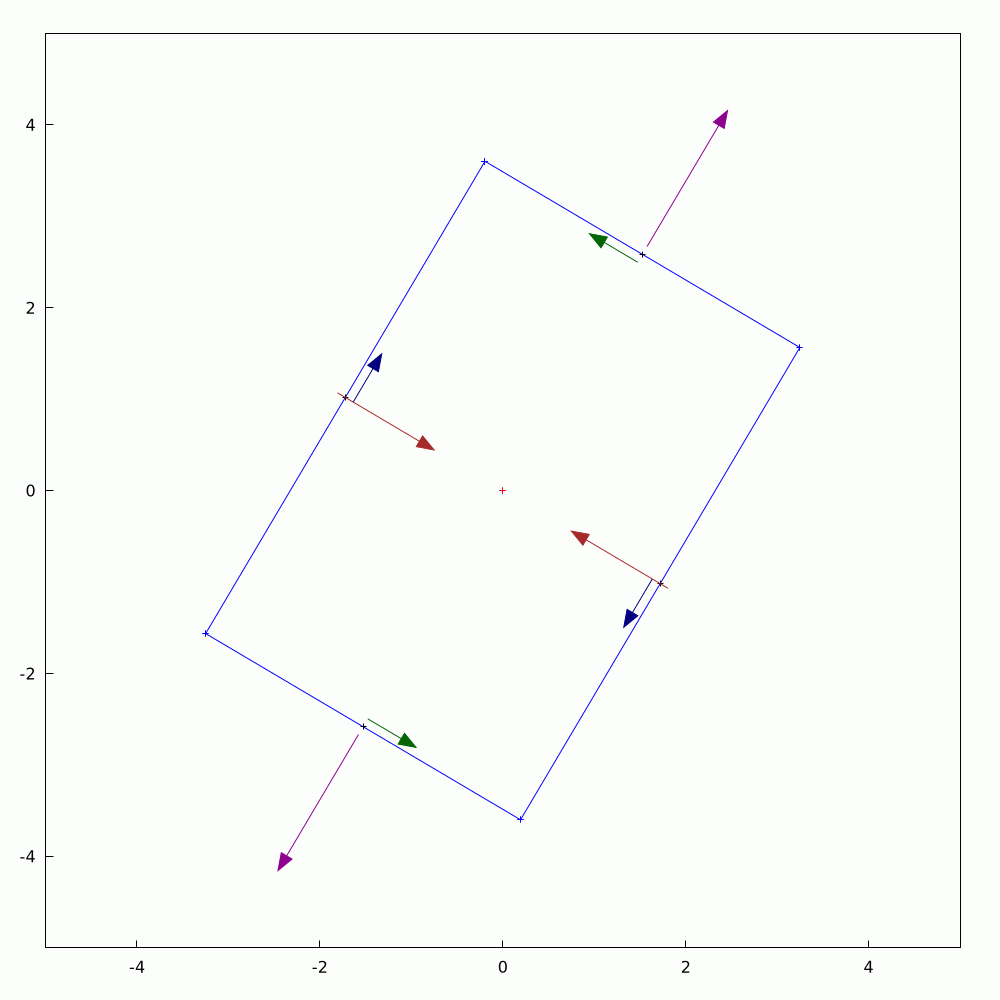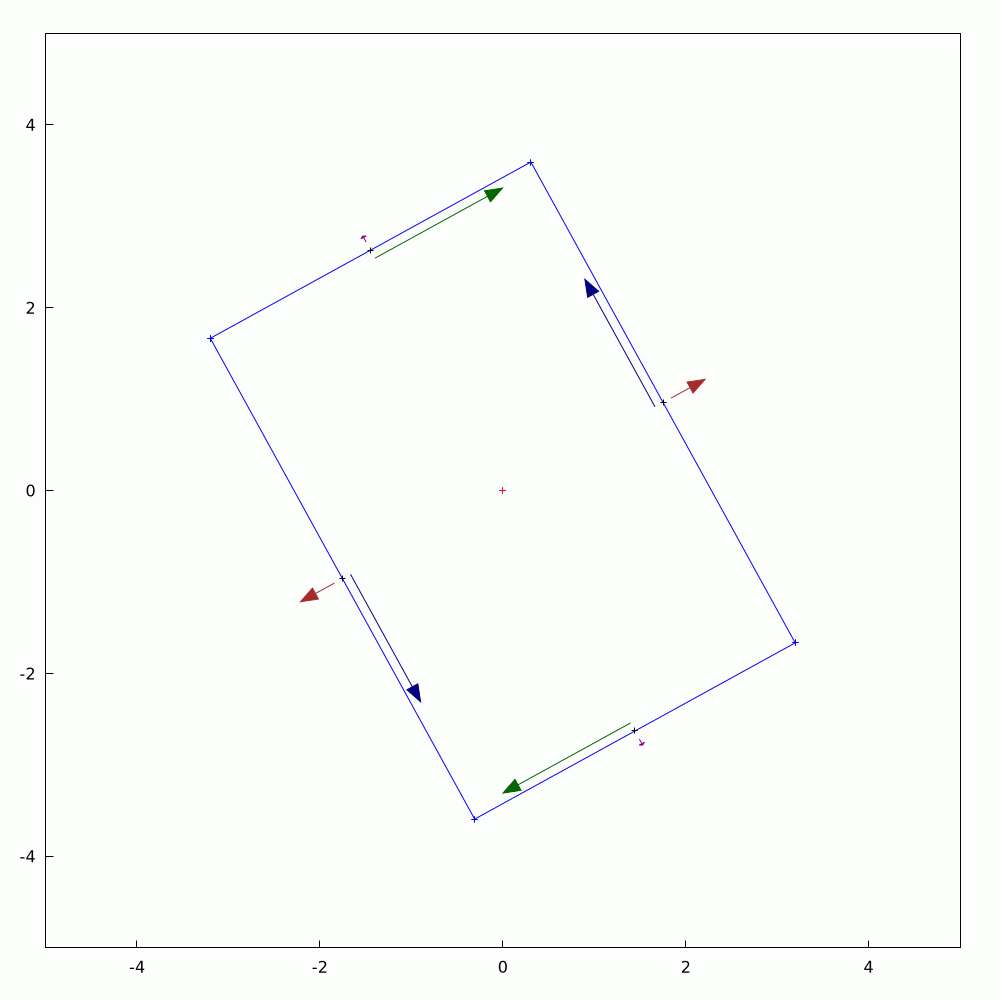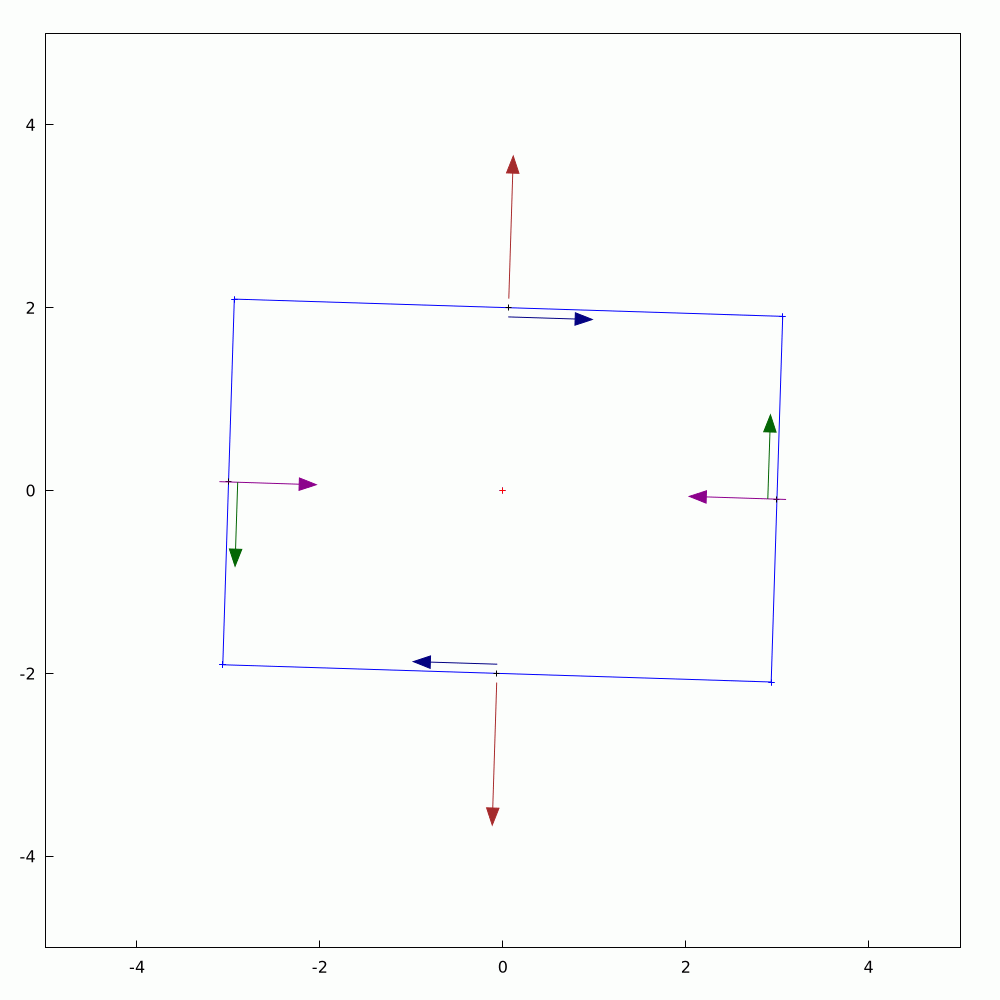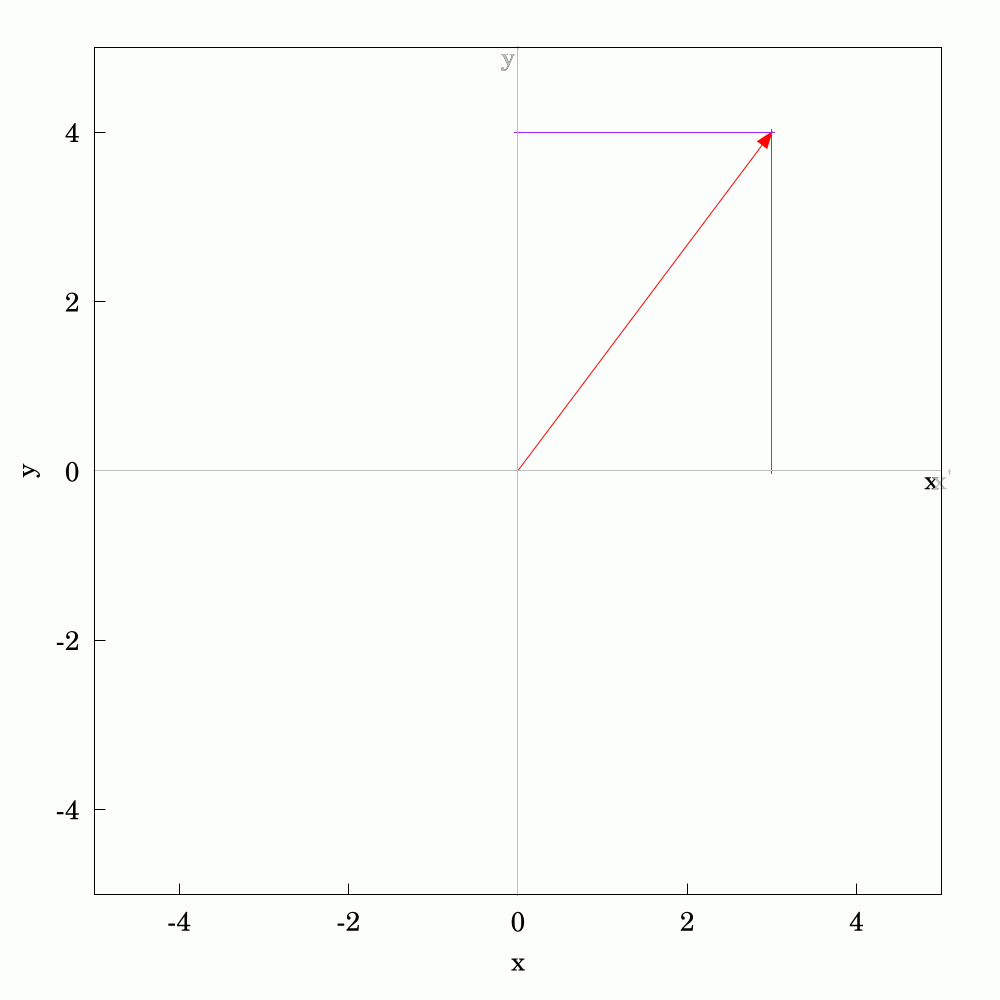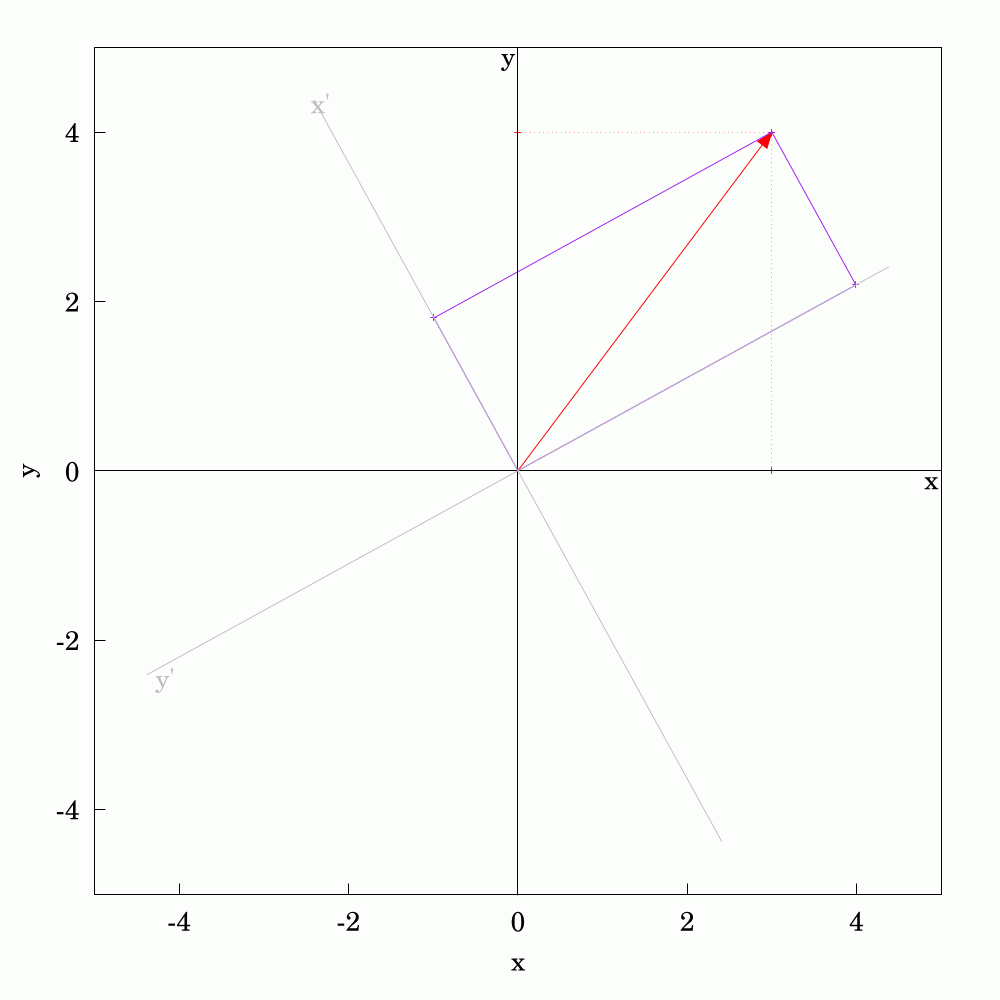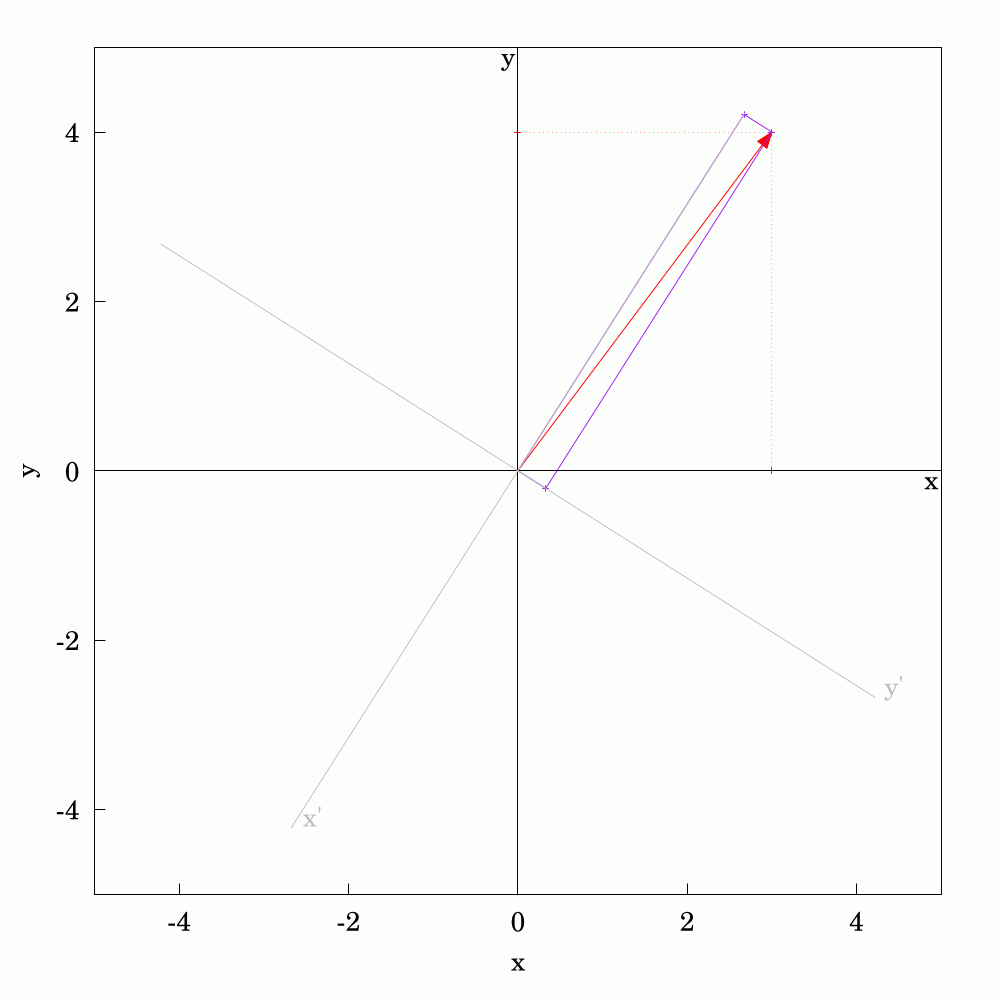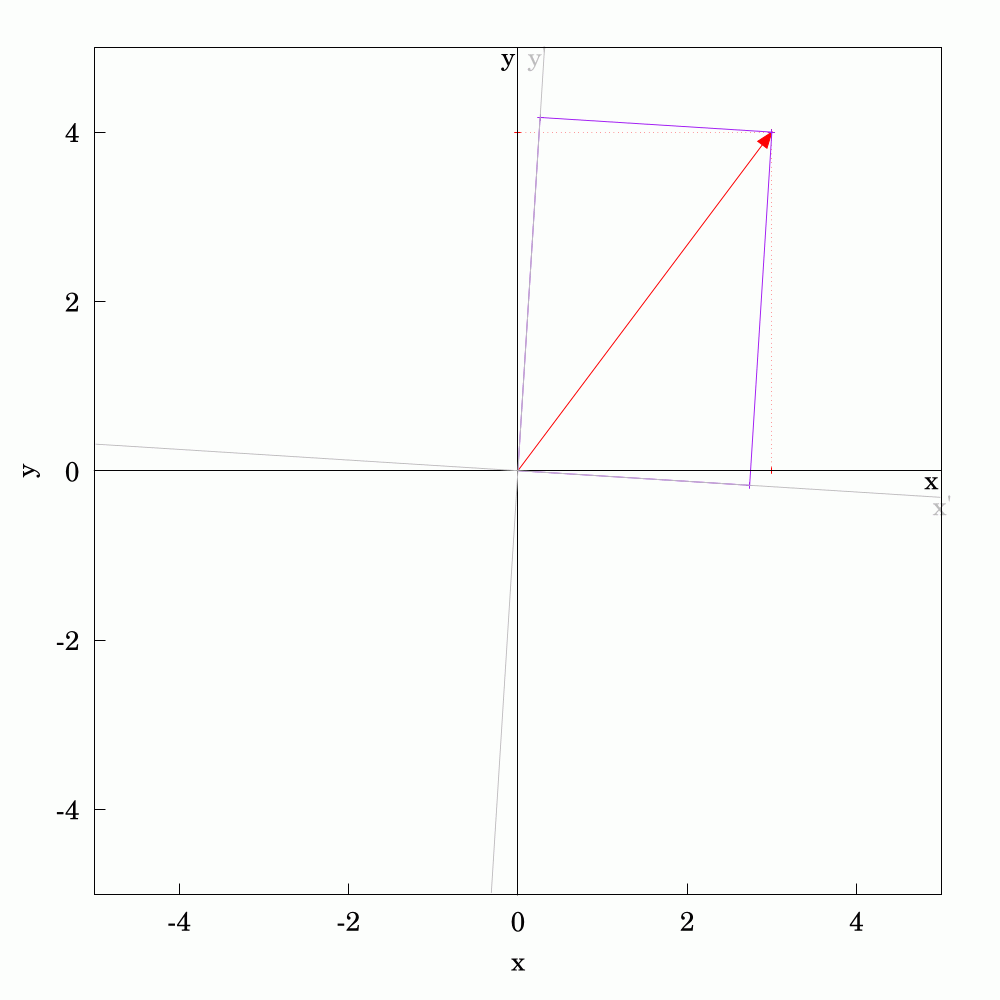
It's straightforward to calculate the #components of a #2D #vector given that you have a pre-defined set of #axes. Often, we talk about #cartesian #coordinates. If the vector changes, whether in #magnitude or #direction, we can calculate the updated components too. The converse question is what if the the vector is held constant and you change or #rotate the axes? The components in the new coordinate system can be found with a little bit of #trigonometry and #algebra. As vectors are #first-order #tensors, they are much simpler to calculate than quantities like stress for which I've also made an animation for if you search for the hashtag #tensors.

In this animation, you can see the components changing as the axes go through a full rotation.

#MyWork #CCBYSA #Mathematics #Mechanics

In the #2D #elasticity, #equilibrium of #stresses can be represented on an infinitesimal rectangular element with components of both #DirectStress and #ShearStress generally acting on all four edges. If you were to rotate the rectangle, the stresses change in a precisely orchestrated fashion. In the orientation where the shear stress components vanish, we get what are called #PrincipalStresses and they and their directions can be ascertained precisely through #eigenvalue analysis. This little graphical demonstration shows one example of such a state. The #AnimatedGif was produced a routine written in #WxMaxima.

#Mathematics #TheoryOfElasticity #Mechanics #SolidMechanics #Engineering #MyWork #CCBYSA #WorkInProgress

Échafaudages

Nuages

2D ou 3D ?

#Image #photo #photos #2D #3D #voir #regarder #vue