It may be a bit soon but I've produced a #calendar for #2025. Unlike previous editions, which featured some of my photographs, this one contains #illustrations to do with #mathematics, #geometry, #physics and #engineering applications.
2 Likes
It may be a bit soon but I've produced a #calendar for #2025. Unlike previous editions, which featured some of my photographs, this one contains #illustrations to do with #mathematics, #geometry, #physics and #engineering applications.

Yesterday, I posted an image of the #LorenzAttractor showing the evolution of three trajectories (shown in red, green and blue) starting close together. Here, I've made it into a little animation to show how the paths initially stay close to each other but after about a quarter of the duration plotted, they #diverge from each other irrevocably (i.e. become uncorrelated) but remain part of the #ChaoticAttractor.
#DynamicalSystems #ChaoticAttractors #StrangeAttractors #NumericalSolutions #Mathematics #AppliedMathematics #CCBYSA #FreeSoftware #WxMaxima
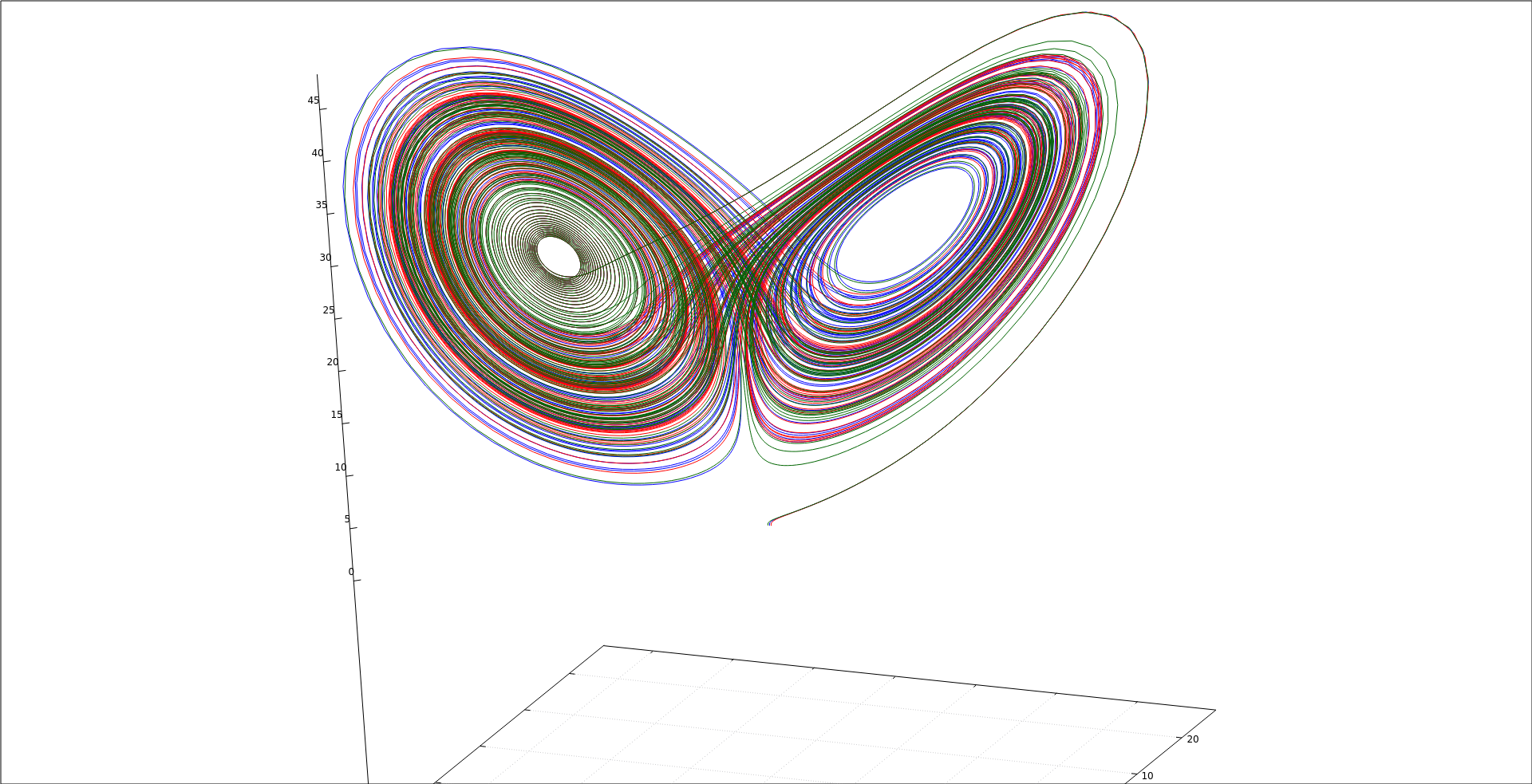
Just messing about a bit. Here is the famous #LorenzAttractor plotted using #WxMaxima. The three #trajectories, shown in red, green and blue are for three fairly nearby #InitialConditions.
#DynamicalSystems #ChaoticAttractors #StrangeAttractors #NumericalSolutions #Mathematics #AppliedMathematics #CCBYSA #FreeSoftware
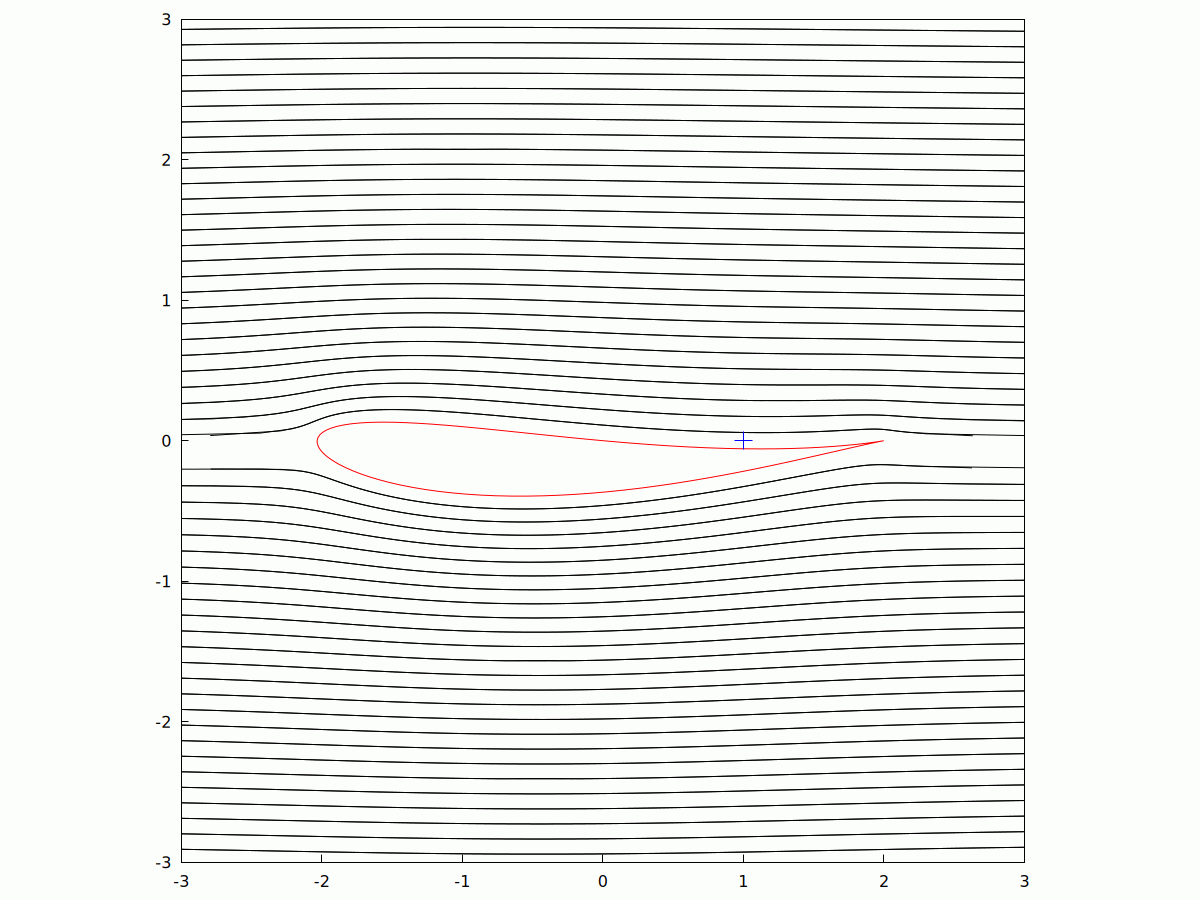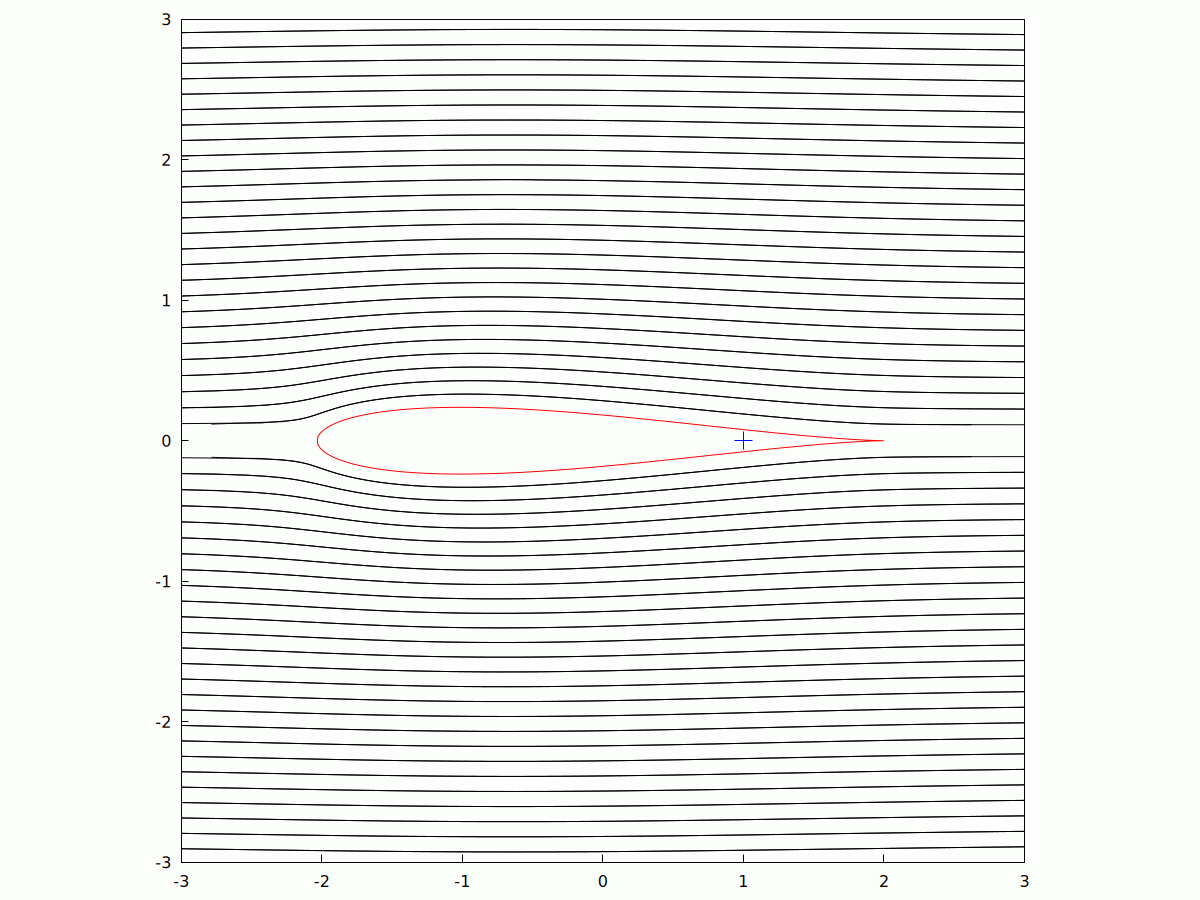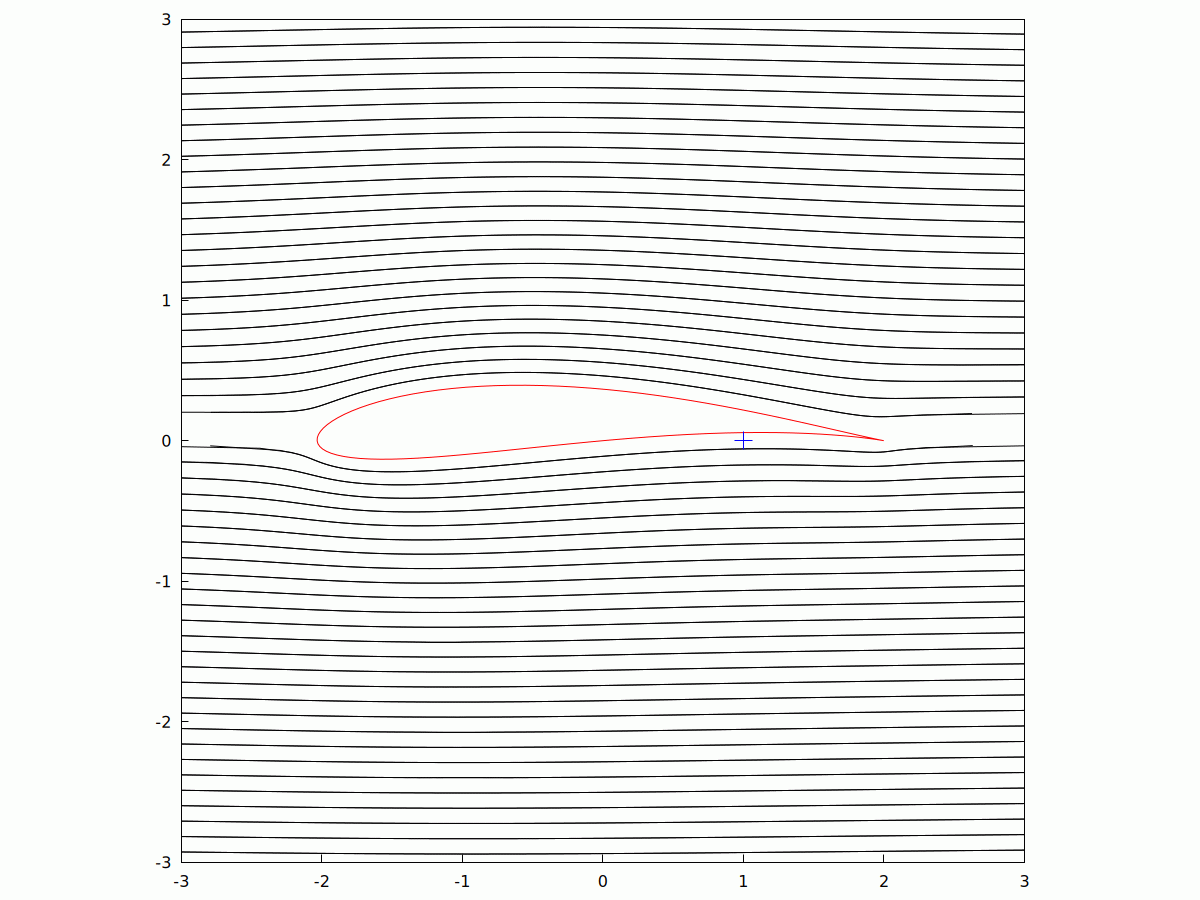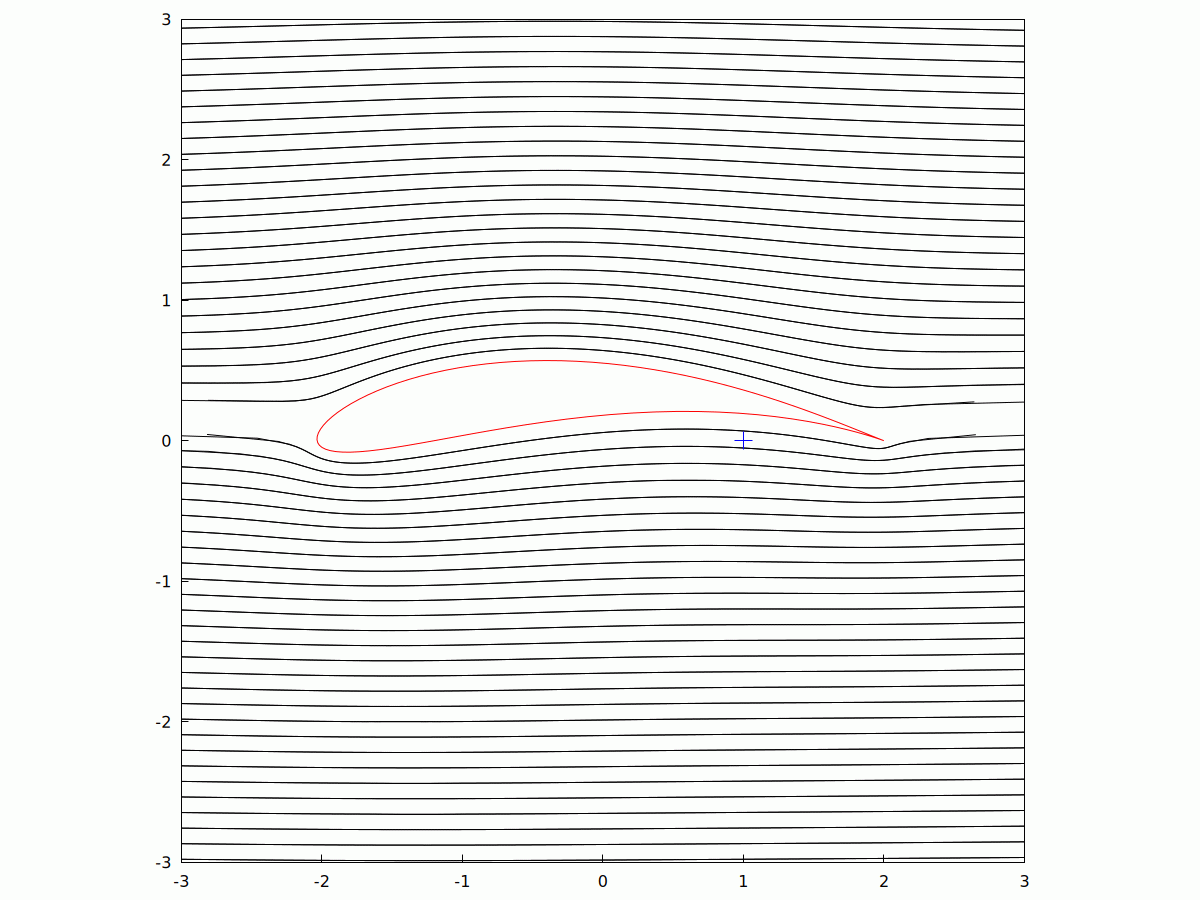
The #Zhukovsky #Aerofoil (sometimes transliterated as #Joukowsky from #Russian), is a 2D model of #streamlined #Airflow past a #wing. It uses #ComplexVariable and is an #AnalyticFunction (i.e. #Differentiable everywhere, save at isolated #Singularities). Take a circle in the #ComplexPlane which is not quite centred at the #origin but passes through the #coordinate (1,0) or (z=1+0i). Using the mapping w -> z+1/z, you get something that looks remarkably like an #aerofoil.
It is a #ConformalMapping meaning that angles are preserved during the mapping. In this animation, I've varied the imaginary part of the the eccentricity, while keeping the real part the same. With a zero #AngleOfAttack, you can see the change in the airflow around the #wing as its shape changes.
#MyWork #CCBYSA #AppliedMathematics #WxMaxima #FreeSoftware #Aeronautics #Aerodynamics #LaminarFlow
A high-speed road or railway track that is poorly designed. The vehicle moves at constant speed from the straight segment of road or track directly onto a CircularArc and thereby encounters an instantaneous application of centripetal acceleration. This is neither good for the driver and passengers who will feel a sudden force outwards, nor for the vehicle which my skid and impose large stress changes in the axles and bearings.
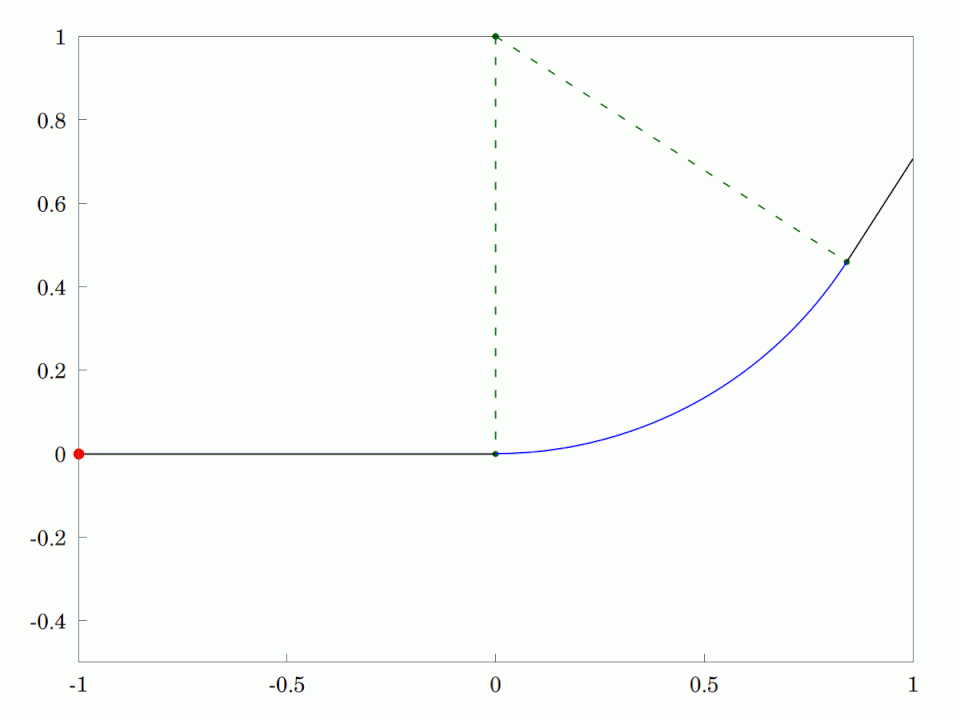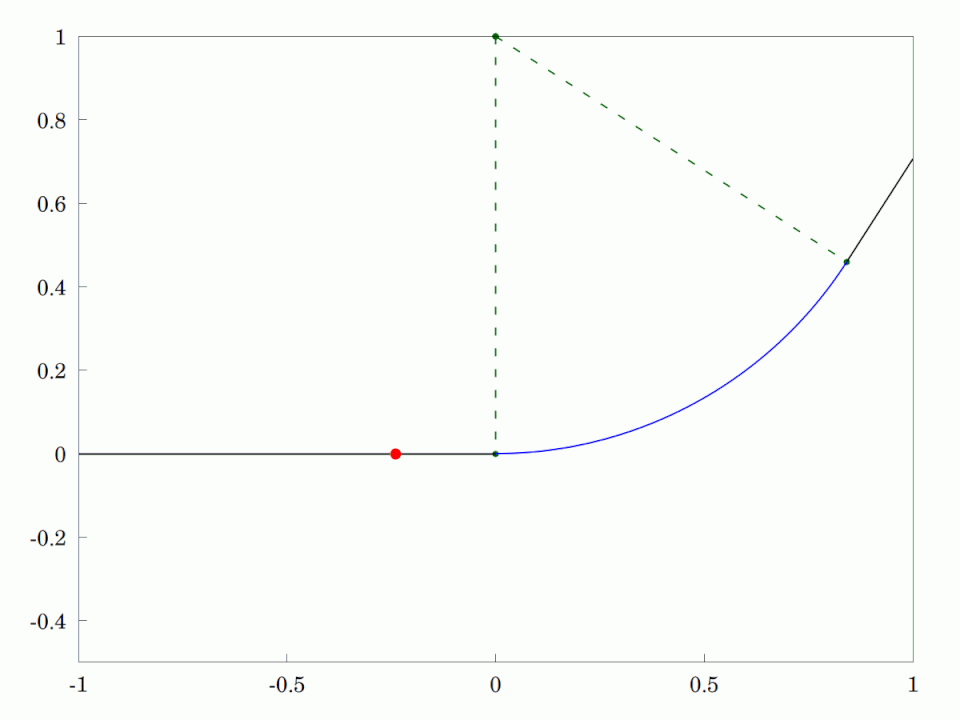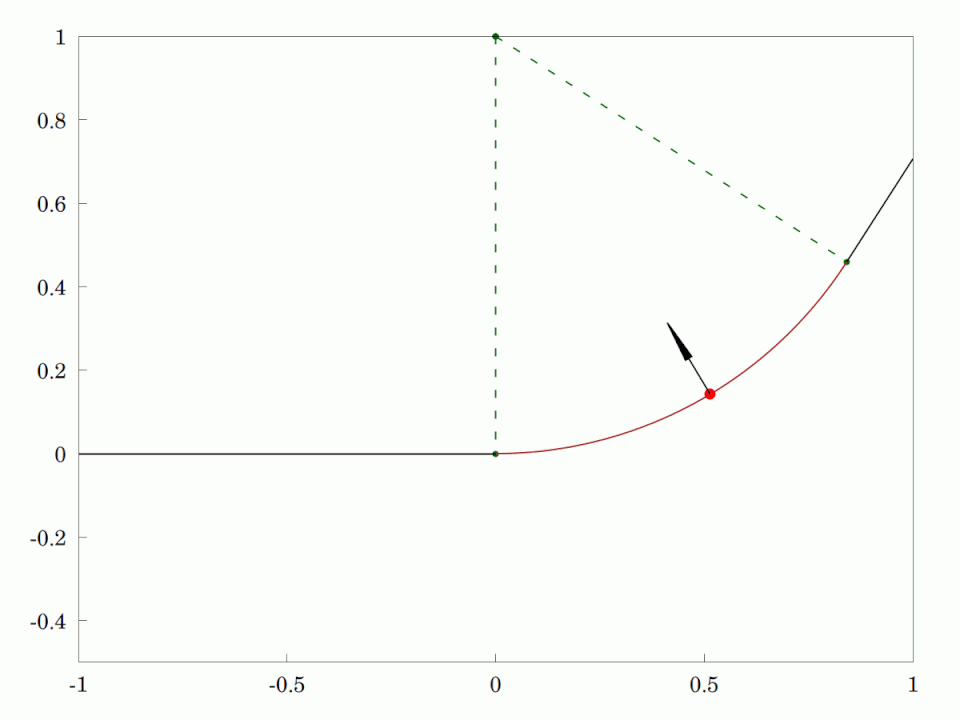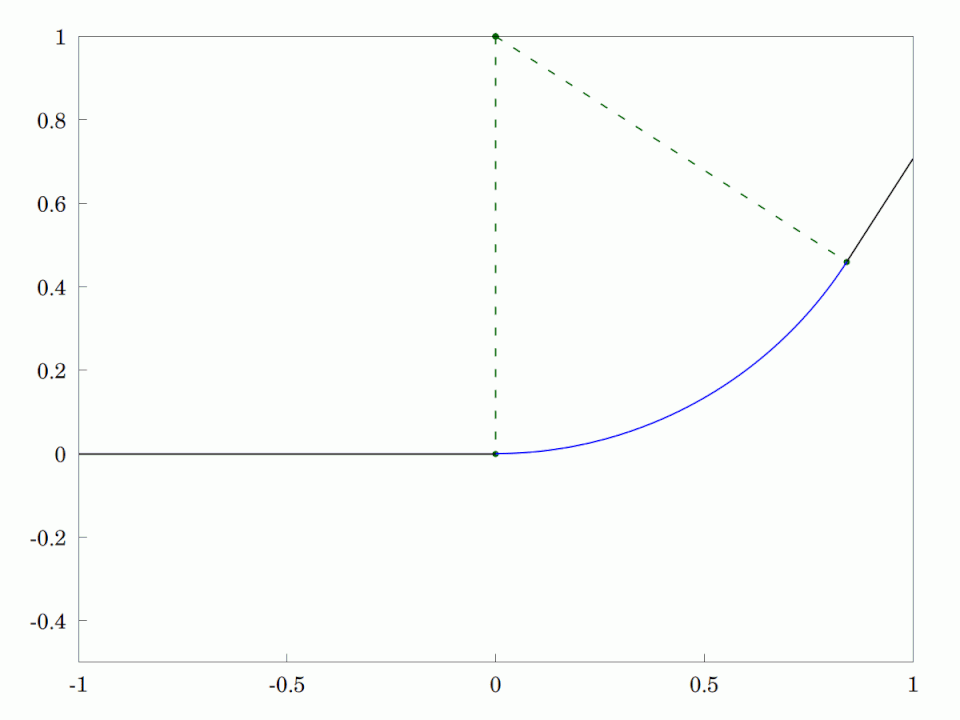
This is why #Engineers use #TransitionCurves in the form of #CornuSpirals or #Clothoids to connect from the straight segment onto a circular arc. It has the property that it starts with zero #curvature at the beginning and then the curvature increases linearly with distance travelled along the curve. At the appropriate curvature, it is connected to a circular arc with the same curvature. The people in the vehicle and the vehicle itself are much less stressed by this solution.

#MyWork #WxMaxima #CivilEngineering #HighwayEngineering #CCBYSA
Forgive the recent apparent obsession (I'd call it a fascination) with the #cycloid but I've just discovered something I'd not heard of before. It is also called a #TautochroneCurve or #Isochrone curve, which means that a particle starting from any location on the curve will get to the #MinimumPoint at precisely the same time as a particle starting at any other point.
Here's an #animation I wrote today in #Maxima which illustrates the property.

#Dynamics #Kinematics #Mathematics #AppliedMathematics #Mechanics #ClassicalMecanics #WxMaxima #FreeSoftware #MyWork #CCBYSA
A couple of weeks ago, I posted an #animation of a point on a circle generating a #cycloid.
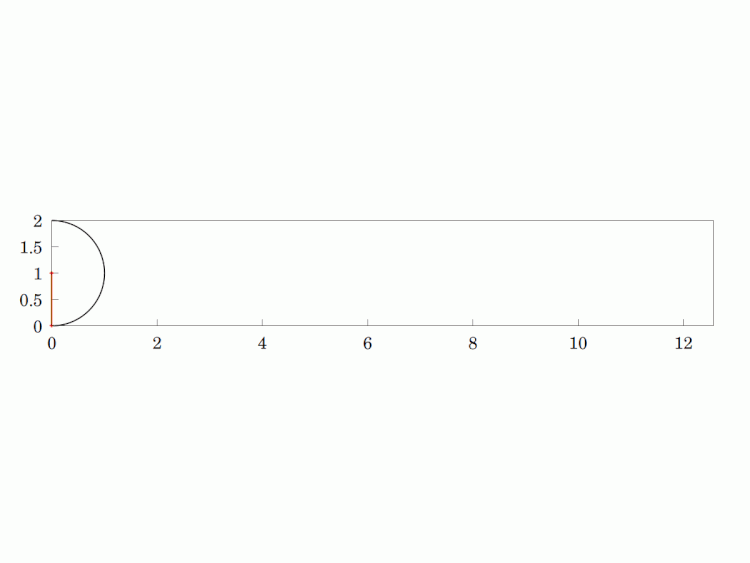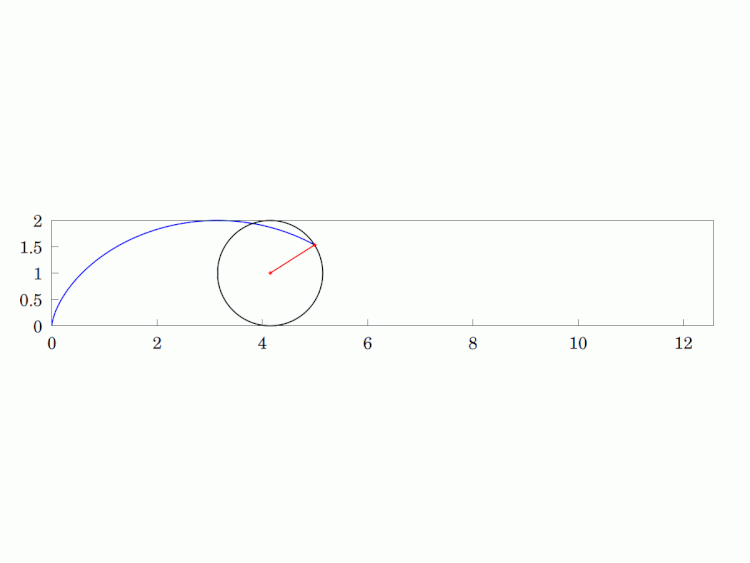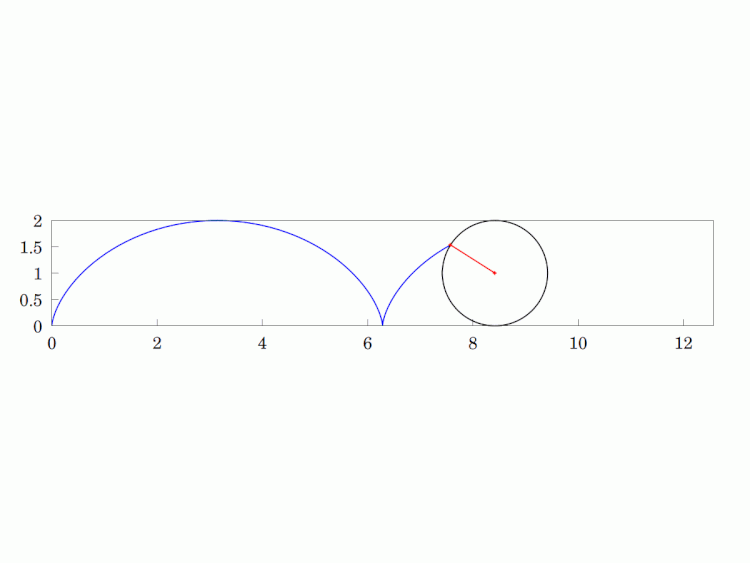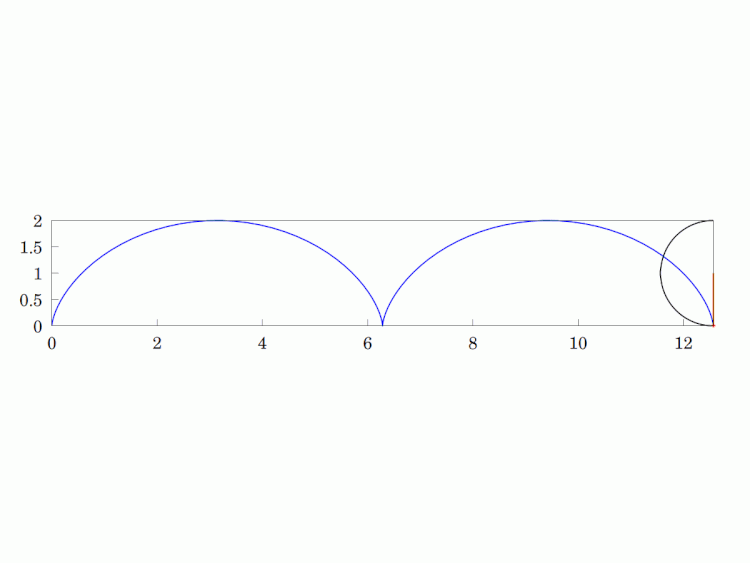
If you turn the curve "upside down", you get the #BrachistochroneCurve. This curve provides the shortest travel time starting from one cusp to any other point on the curve for a ball rolling under uniform #gravity. It is always faster than the straight-line travel time. This is an interesting problem in #ClassicalMechanics and exercised luminaries like #Newton and #Euler. I think the latter's use of the #CalculusOfVariations is a stroke of genius.
Anyway, the #animation took a bit of thought as it requires a bit of #Mechanics, some #Integration and is made a bit more tricky as the curve is multi-valued and so you need to treat different branches separately. The #AnimatedGif was produce with #WxMaxima.
For some reason that I can't fathom, I'm not finding it possible to upload the graphic and so if you want to see it, please use the link below.
https://drive.google.com/file/d/1edcZnZ_uiaQOQrFB03XHslNUVCmxcSut/view?usp=drive_link
#MyWork #CCBYSA #Mathematics #Maths #AppliedMathematics #Physics #Calculus
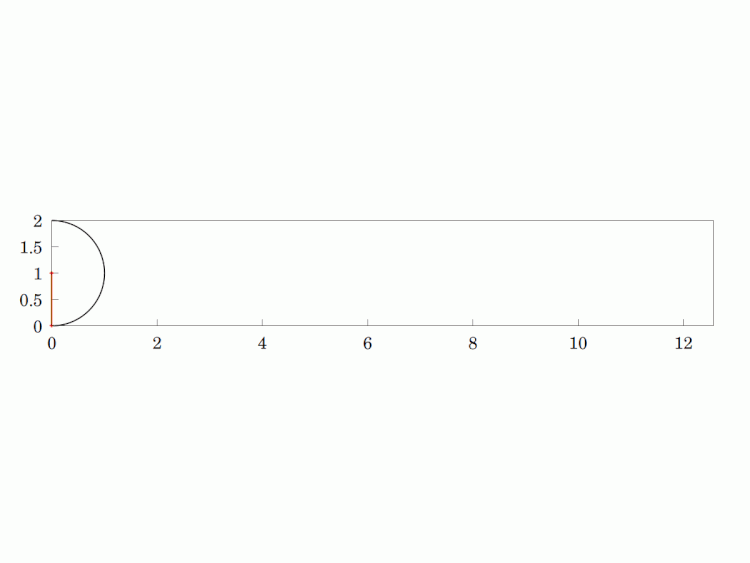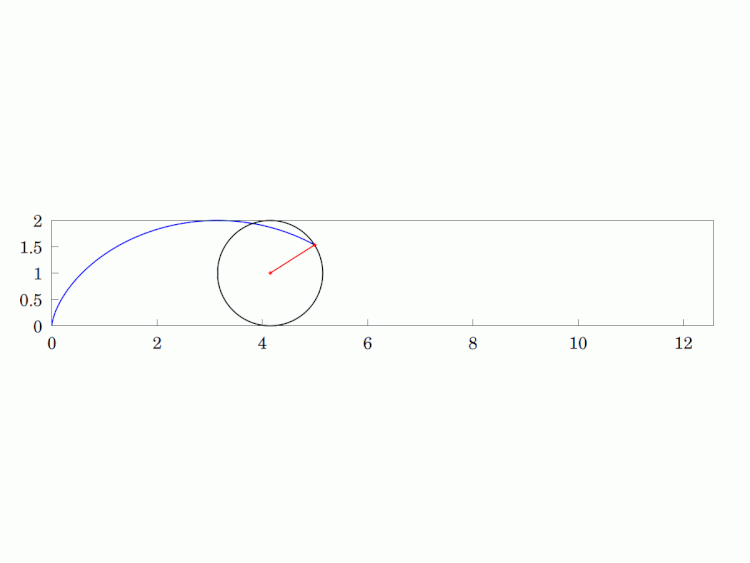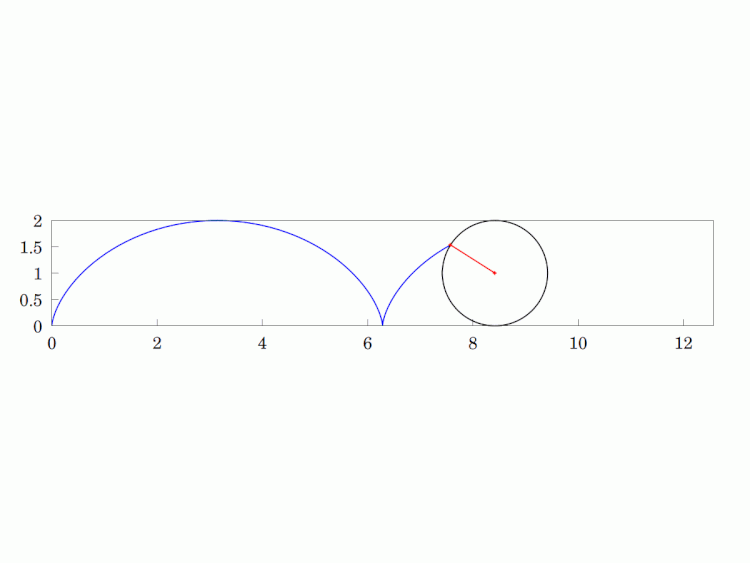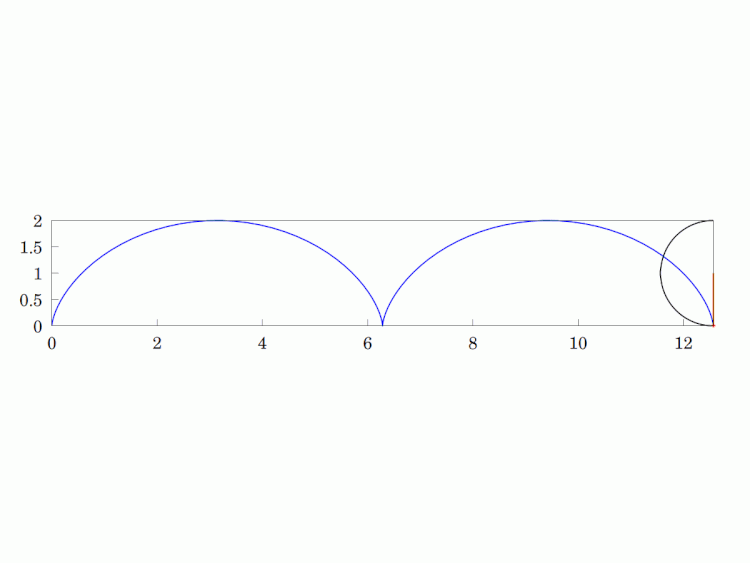
Imagine a circular wheel rolling, without skidding, on a flat, horizontal surface. The #locus of any given point on its #circumference is called a #cycloid. It is a #periodic #curve over a length equivalent to the #circle's circumference and has #cusps whenever the point is in contact with the surface (i.e. the two sides of the curve are tangentially vertical at that point).
Interestingly, it is also the curve that solves the #Brachistochrone problem, which means that starting at a cusp on the inverted curve (maximum height), a frictionless ball will roll under uniform gravity in minimum time from the start to any other point on the curve, even beating the straight line path.
#Mathematics #Geometry #Maths #AppliedMathematics #Mechanics #Kinematics #Dynamics #Physics #MyWork #CCBYSA #WxMaxima

Just a simple demonstration here of the #locus of #StraightLine in ##ThreeDimensionalSpace in #CartesianCoordinateds passing through a known point with #PositionVector a and a direction d. A #Projection onto the x-y plane is also depicted.
#AnimatedGif #FreeSoftware #WxMaxima #Mathematics #Maths #Geometry #MyWork #CCBYSA

A few weeks ago, I posted an example of a #projectile #trajectory in a uniform #GravitationalField without #AirResistance. It's a school-level exercise but it was nice to produce an #animation for it. To model air resistance is a bit more tricky as any #fluid, including #air, is complex and does not necessarily behave as you might expect. A simple model for it might be to assume it is a #linear #viscous fluid offering resistance proportional to the velocity of the projectile, i.e. R = -k.v, where v is the velocity vector and k is a constant which dictates how viscous the fluid is.
Happily, this model has exact solutions so I didn't need to do any numerical integration to find the form of the displacement. Here are four different cases, including the "ideal" case k = 0. The others are k = 0.1, 1 and 10, with the middle one highlighted. The essential difference between the non-resistance case and the others is that horizontal velocity steadily decreases with time and decays towards zero exponentially. The vertical velocity is also reduced but still grows. The most viscous case (k = 10) shows terminal velocity behaviour very quickly and the projectile appears to be moving through treacle.
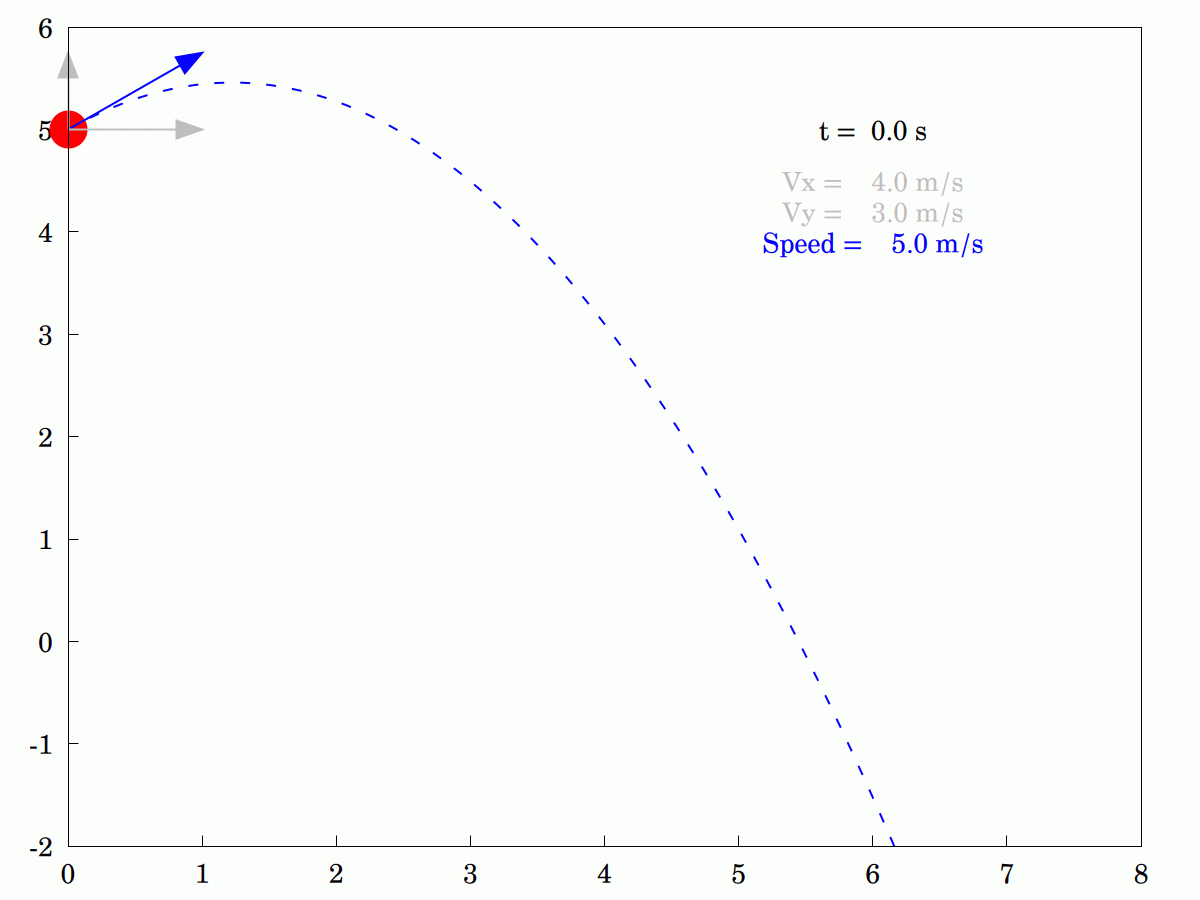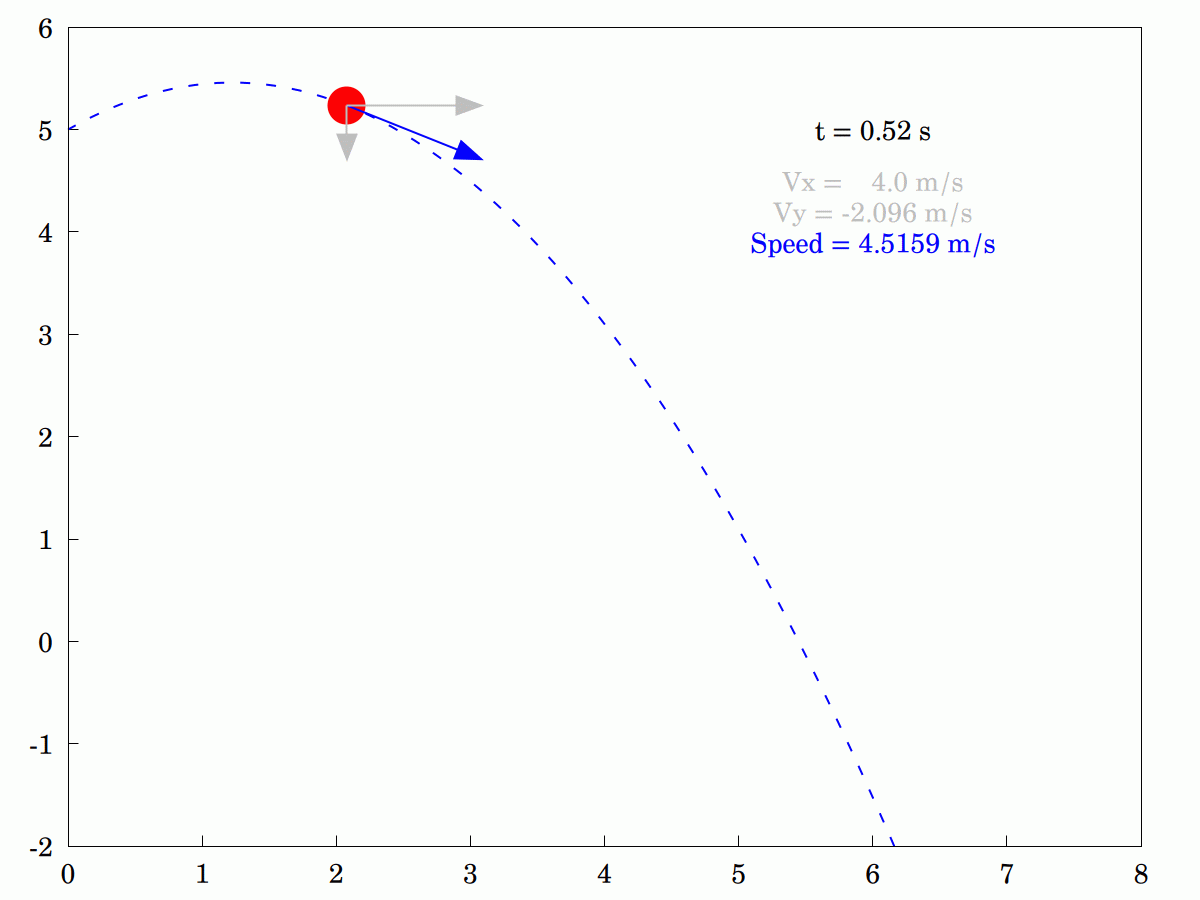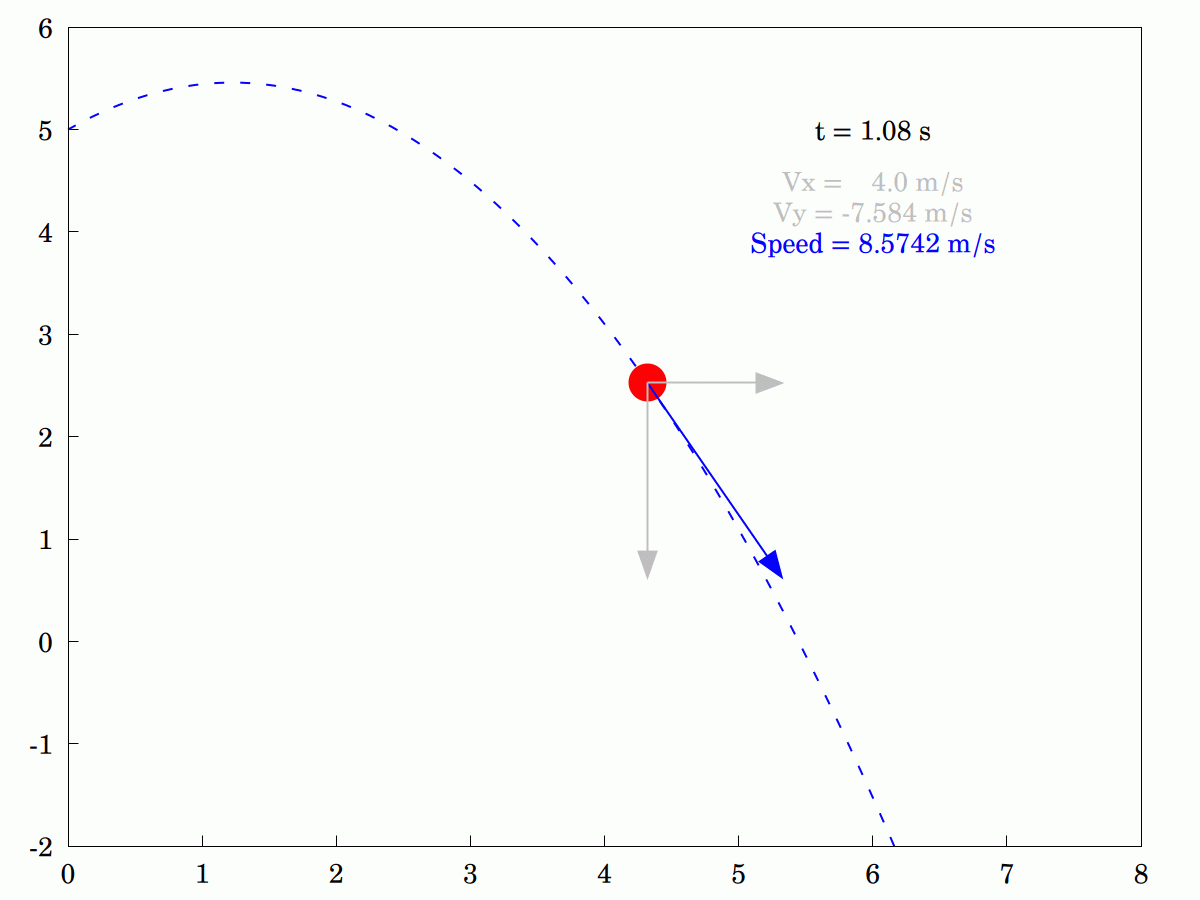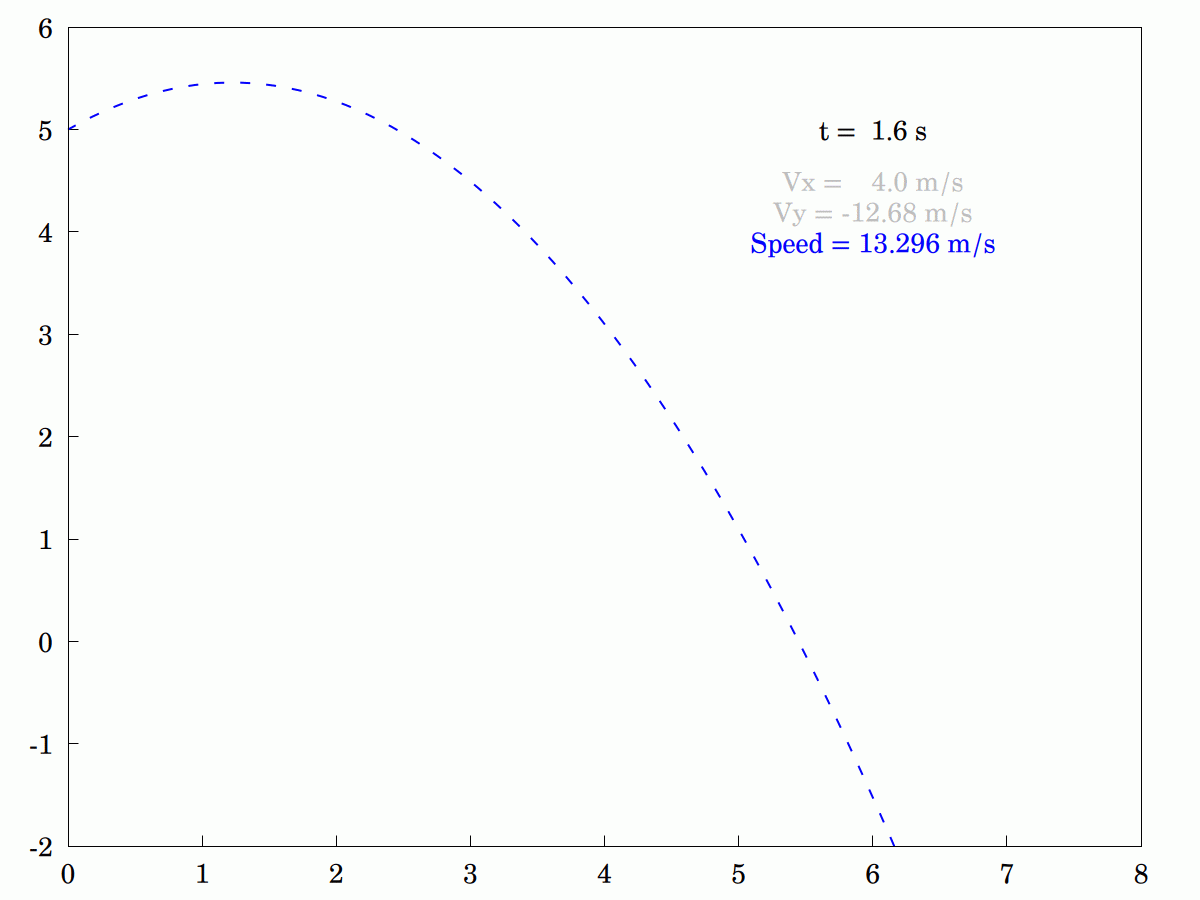
I was explaining to my wife how the #velocity #components of an idealized #projectile differ. She was having some problems understanding that only the #vertical component changes and that the #horizontal component remains constant. In the end, I knocked up this little animation to tr and explain pictorially (the program in #WxMaxima is actually interactive. so you can stop it, step through it or run it backwards if that helps).
#Maths #Mathematics #Mechanics #ConstantAcceleration #Vectors #Dynamics #MyWork #CCBYSA #FreeSoftware
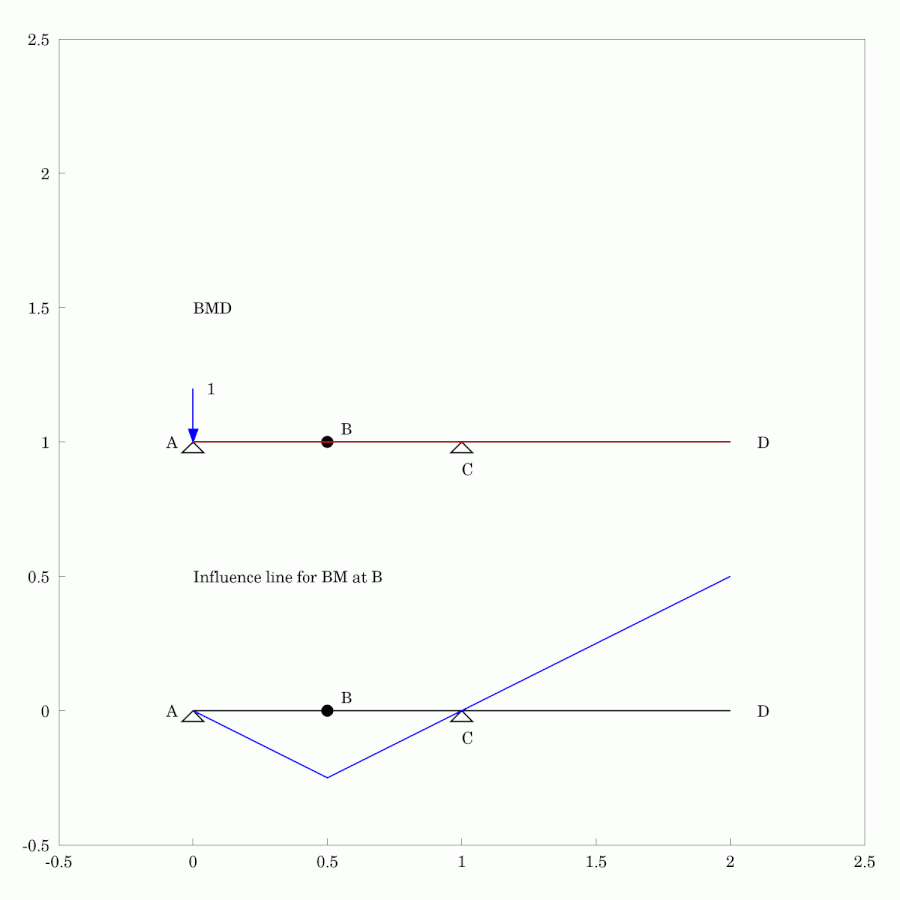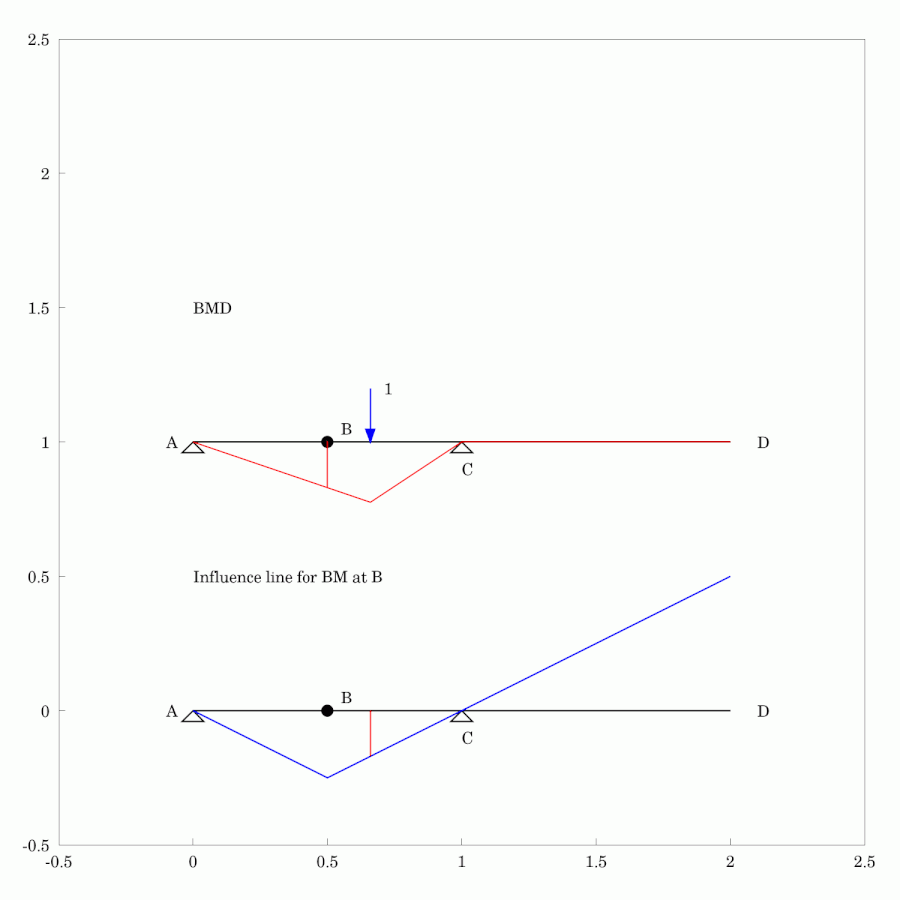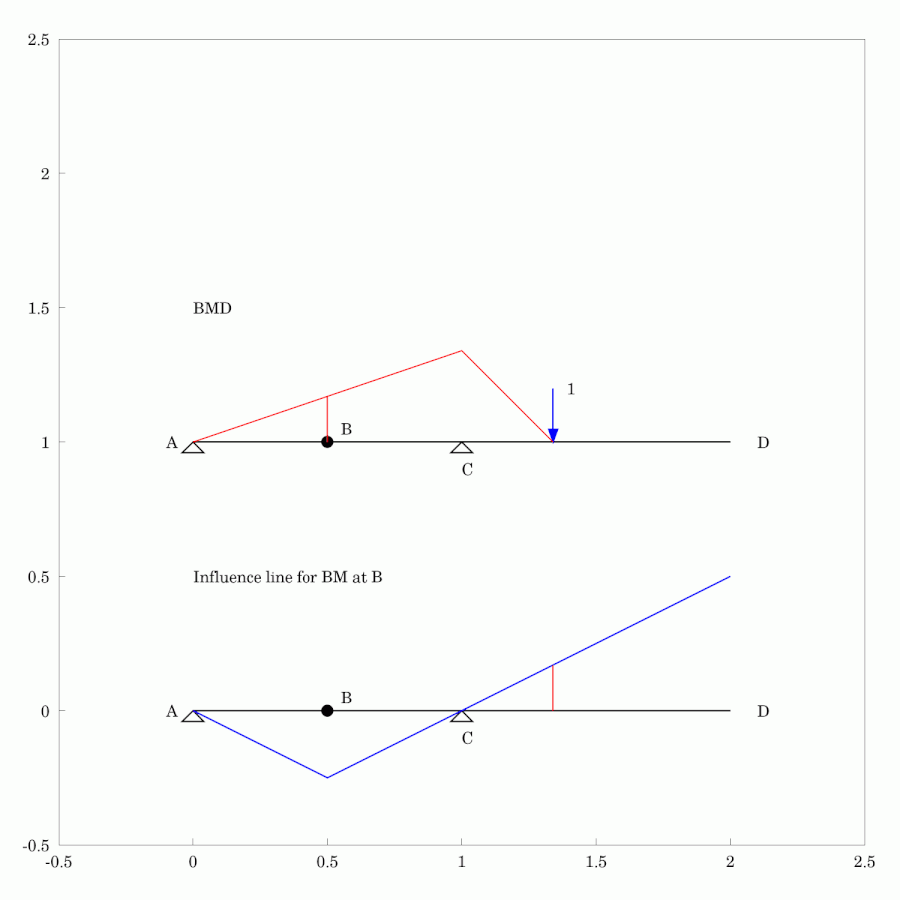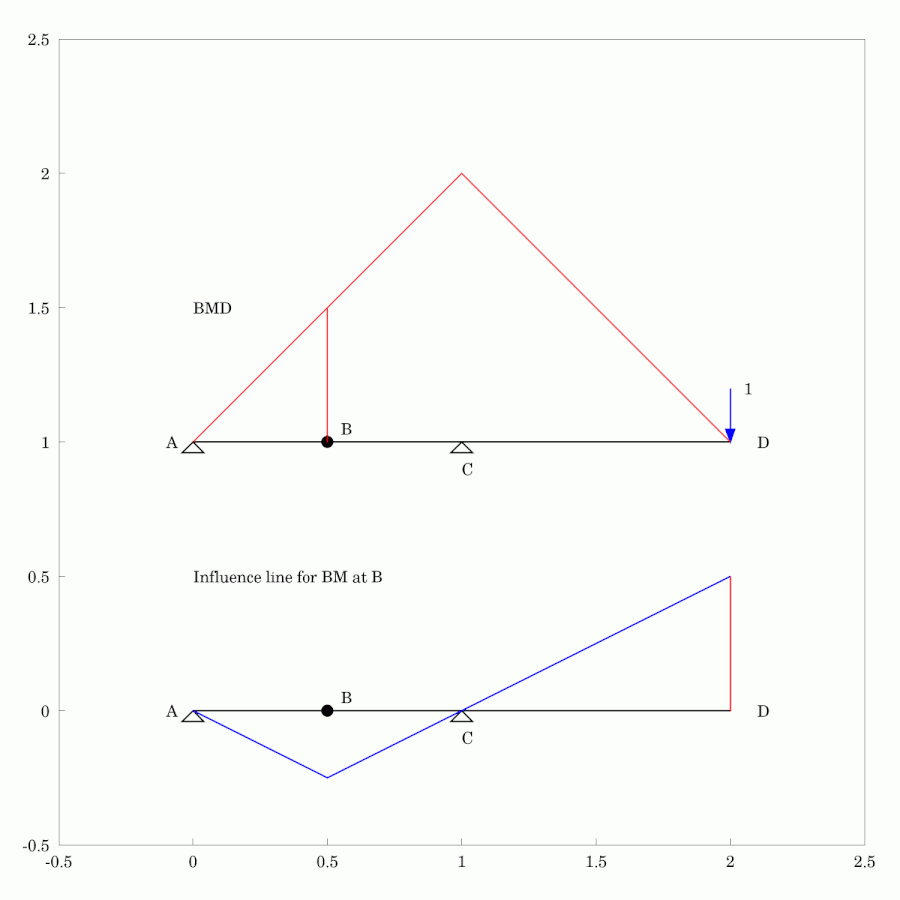
In #StructuralEngineering #Analysis, #InfluenceLines are used to depict the variation of quantity at a particular location as the location of a #Load or #Action is changed. In the #Animation shown, we can see the change in #BendingMoment in a #StaticallyDeterminate #Beam as a unit force moves from one end to the other. Both the #BendingMomentDiagram and the influence line for bending moment at the centre of the left-hand span, B, are shown. The influence line is often used as a tool to determine where the load should be placed to cause the most extreme cases of interest, say for #design purposes.
#MyWork #CCBYSA #WxMaxima #FreeSoftware #AnimatedGif #Engineering
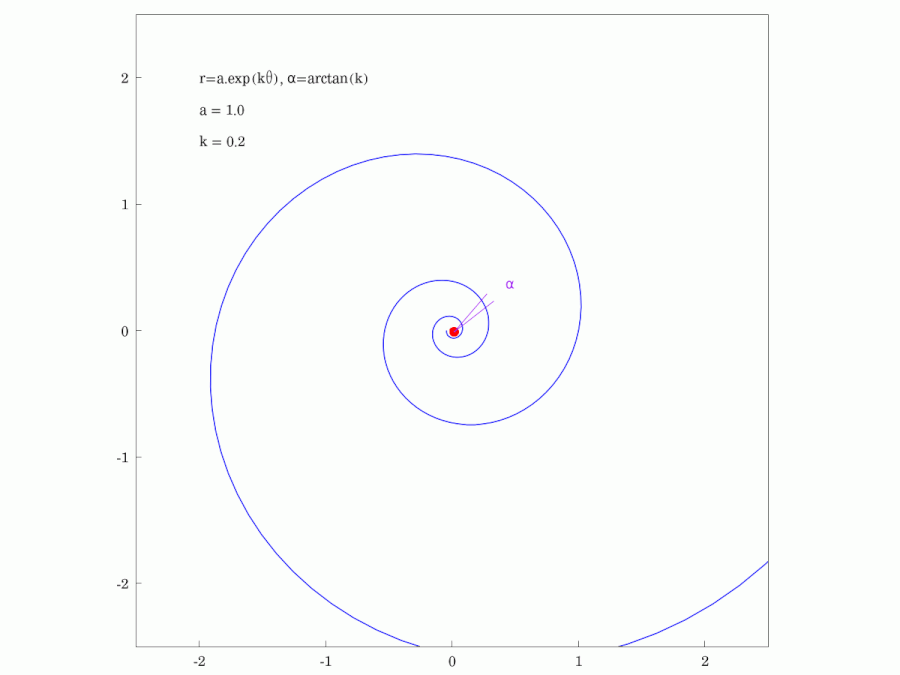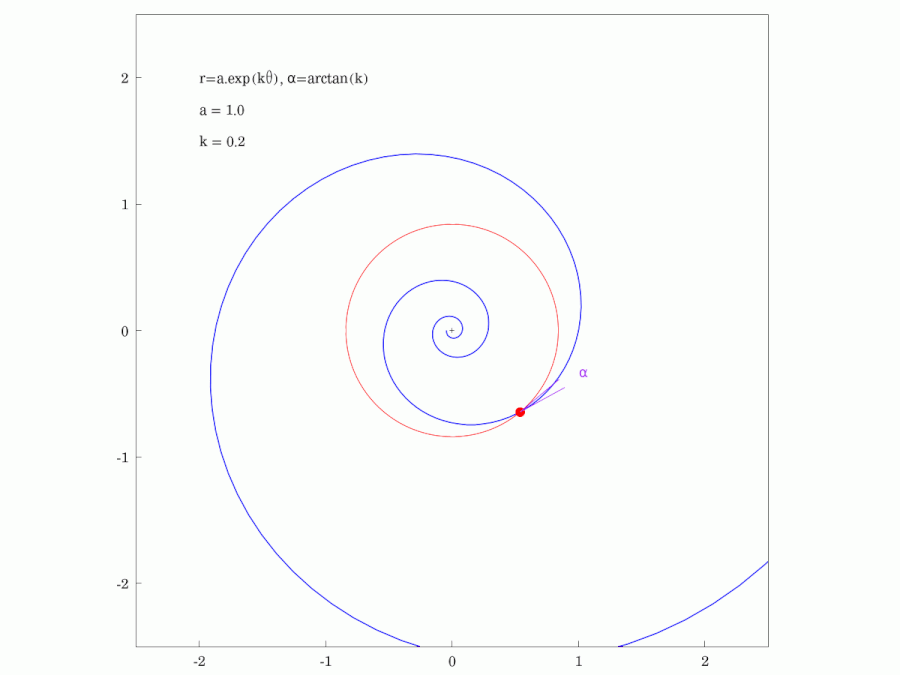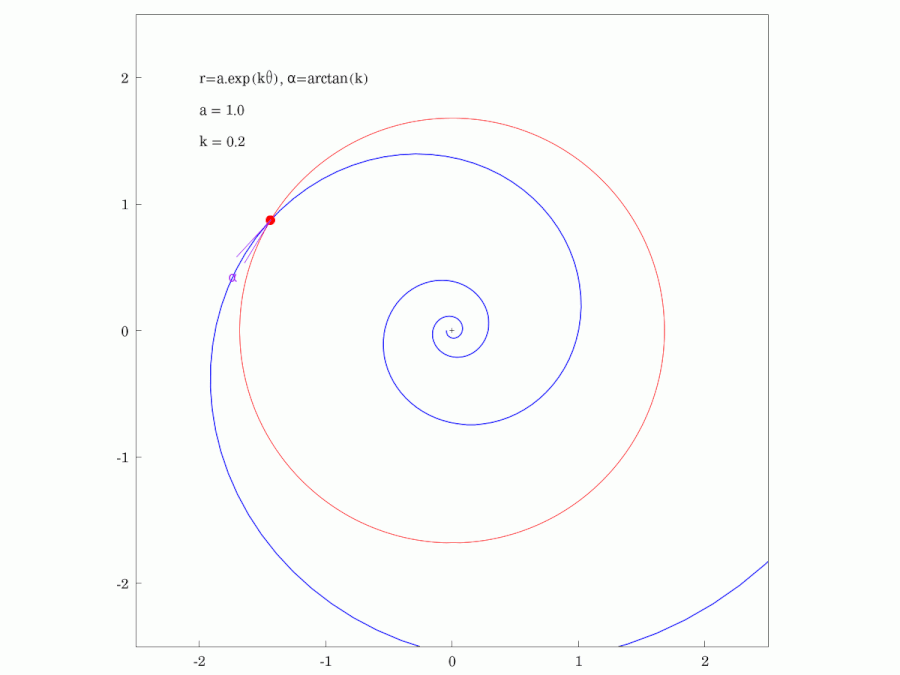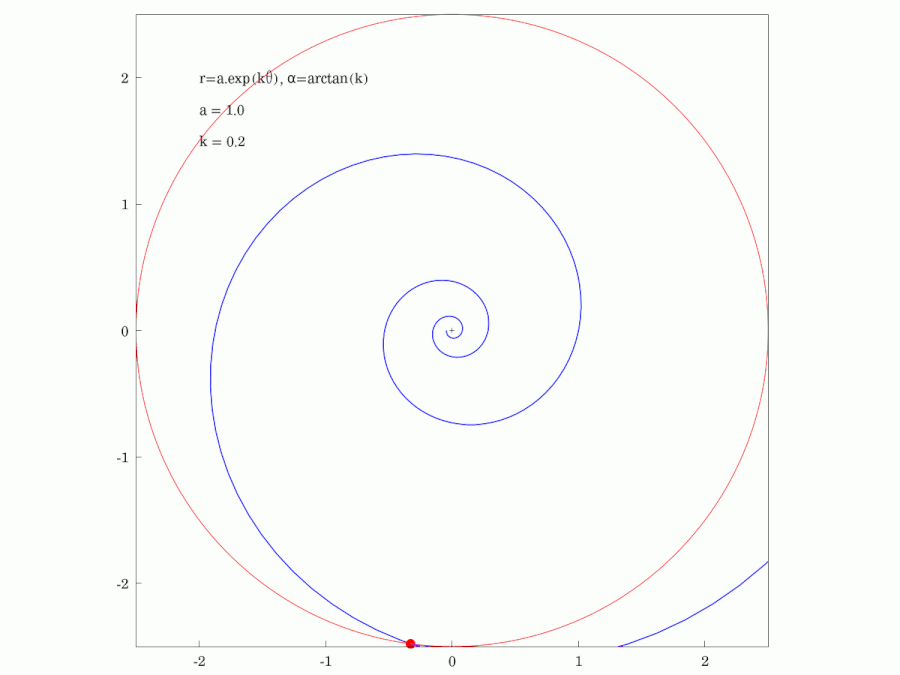
#LogarithmicSpirals are found in many aspects of nature such as in the growth of #snail #shells and the form of #spiral #galaxies. They have a lot of interesting #geometric properties and this #animation highlights just one of them. It shows that the #PolarAngle (here denoted as ⍺) is constant, being the angle that the #tangent of the spiral makes with the tangent of any circle centred at the origin.
#MathsForTheDay #Mathematics #Maths #Geometry #WxMaxima #FreeSoftware
#JohannesKeppler was a brilliant #astronomer who studied the motion of #planets. Like everyone, he also had some strange ideas about the heavens, no doubt as a person in the middle ages would about the harmony of worlds and their purported relation to things like the #PlatonicSolids, which was of course bogus. He is probably best known for his famous three laws of #PlanetaryMotion which he reluctantly formulated when he had to abandon the idea that planets only orbit the #Sun in perfect #circles.
His First Law says that planets orbit the Sun in an #ellipse with the Sun at one #focus. Of course, a circle can be thought of as an ellipse where the two #foci have coalesced into one point (zero eccentricity). Here is what the orbit would look like in that case. The angular velocity of the planet is constant in this case and the areas swept out in equal times are identical.
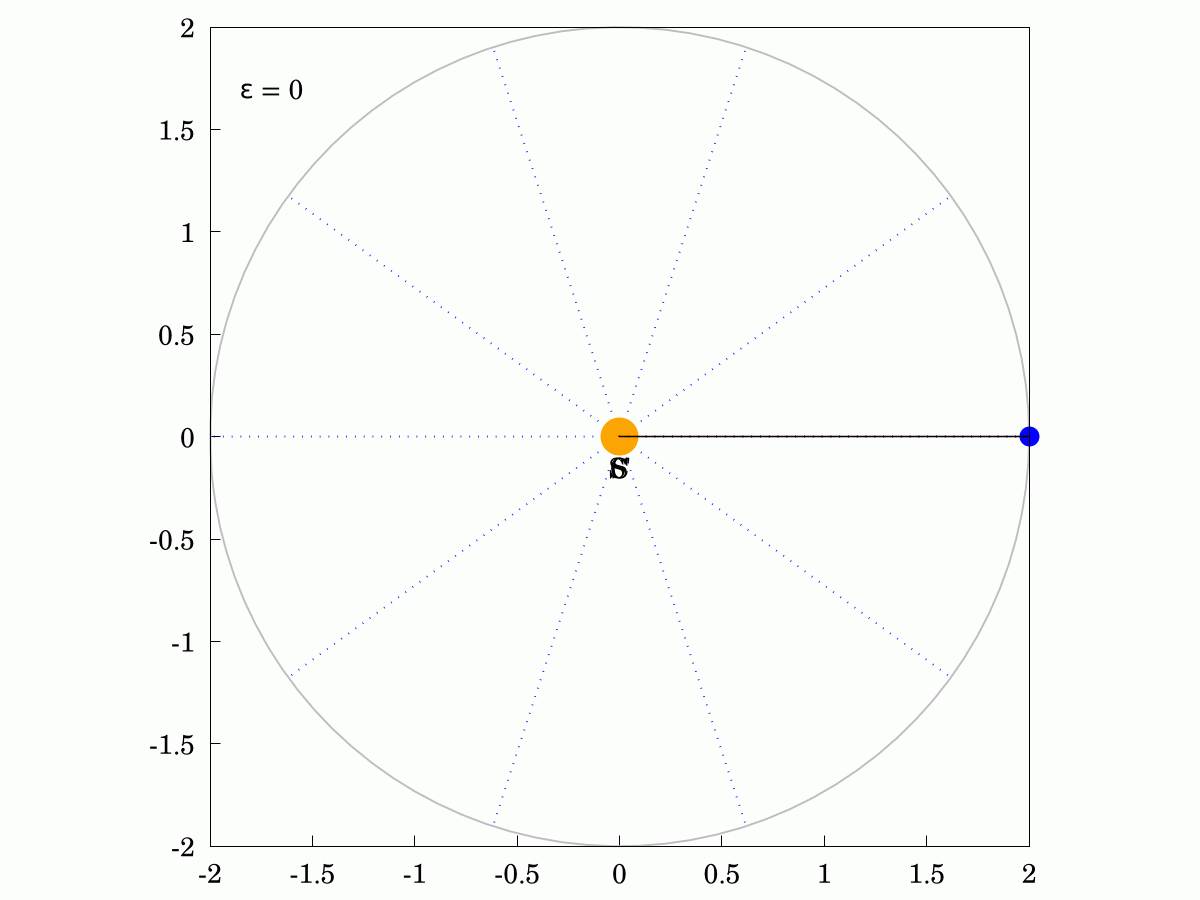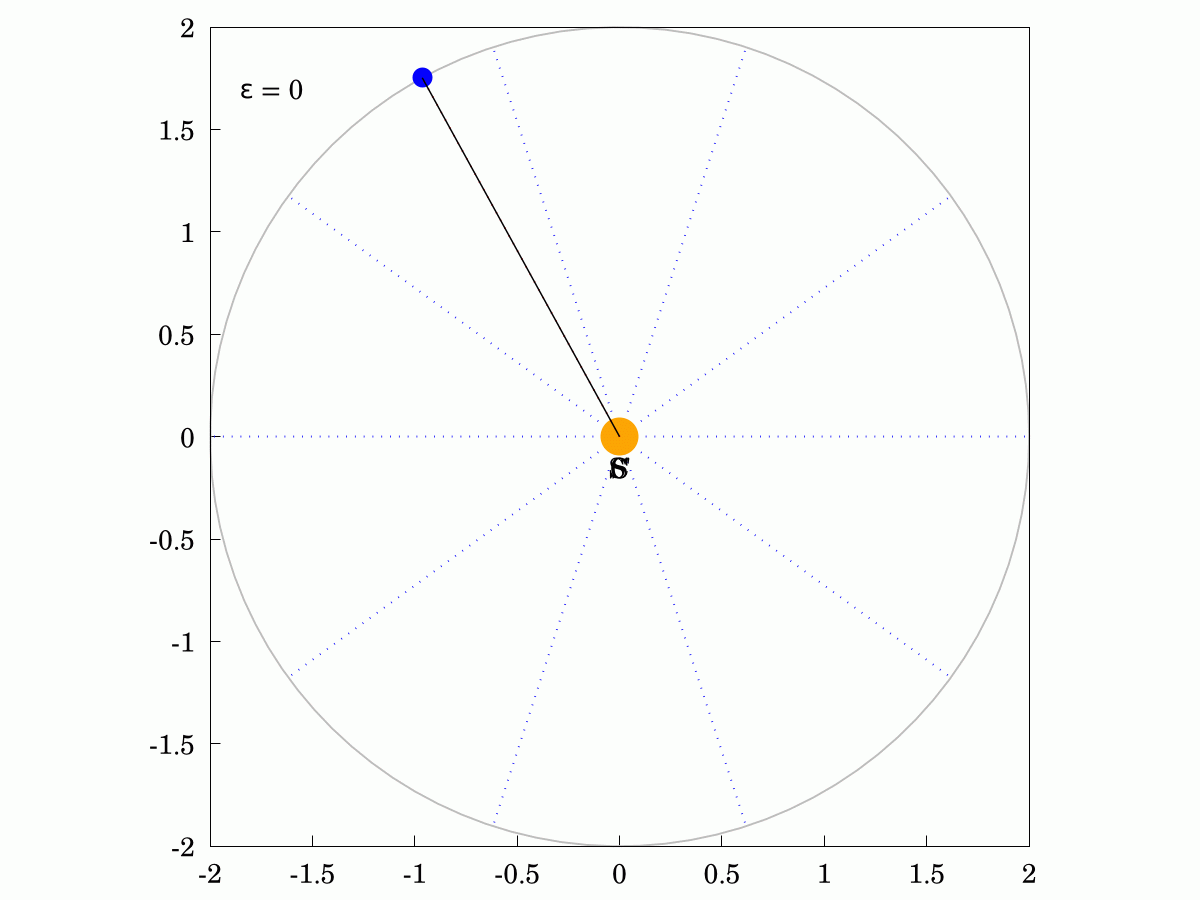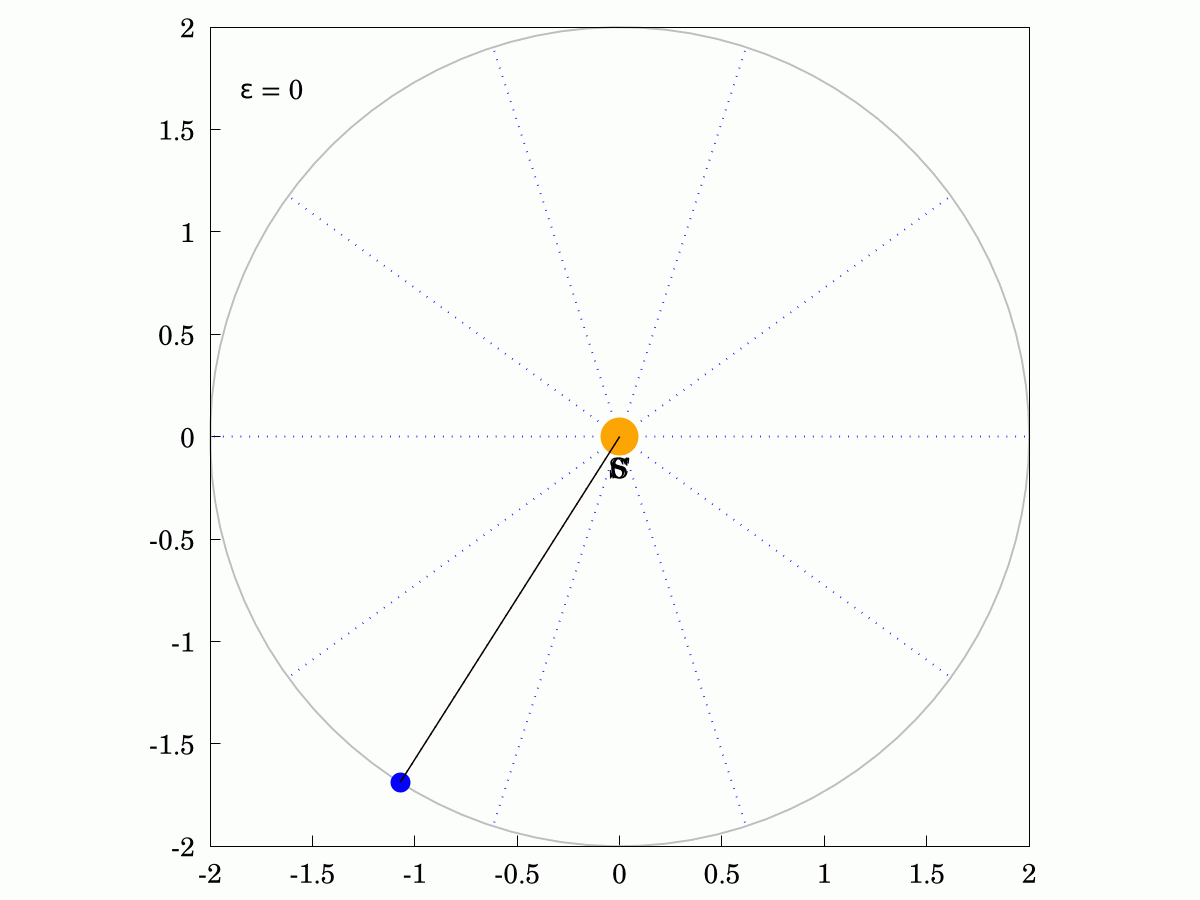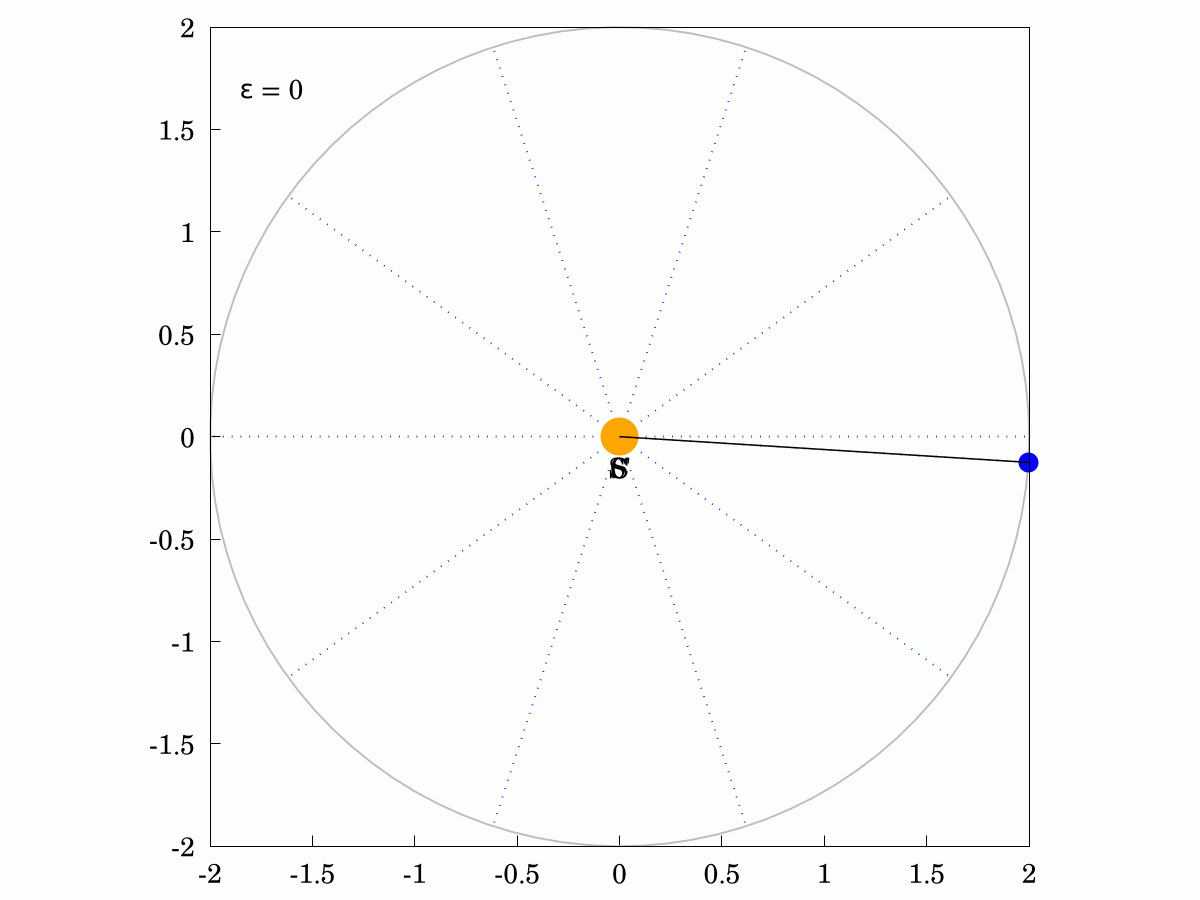
#Keppler's Second Law states that the areas swept out in equal times are always identical, even for eccentric ellipses. Here are two examples and you can show that the areas of all the sectors in each case are identical. The Sun is labelled S, the other focus is labelled S' and the centre of the orbit is labelled C.
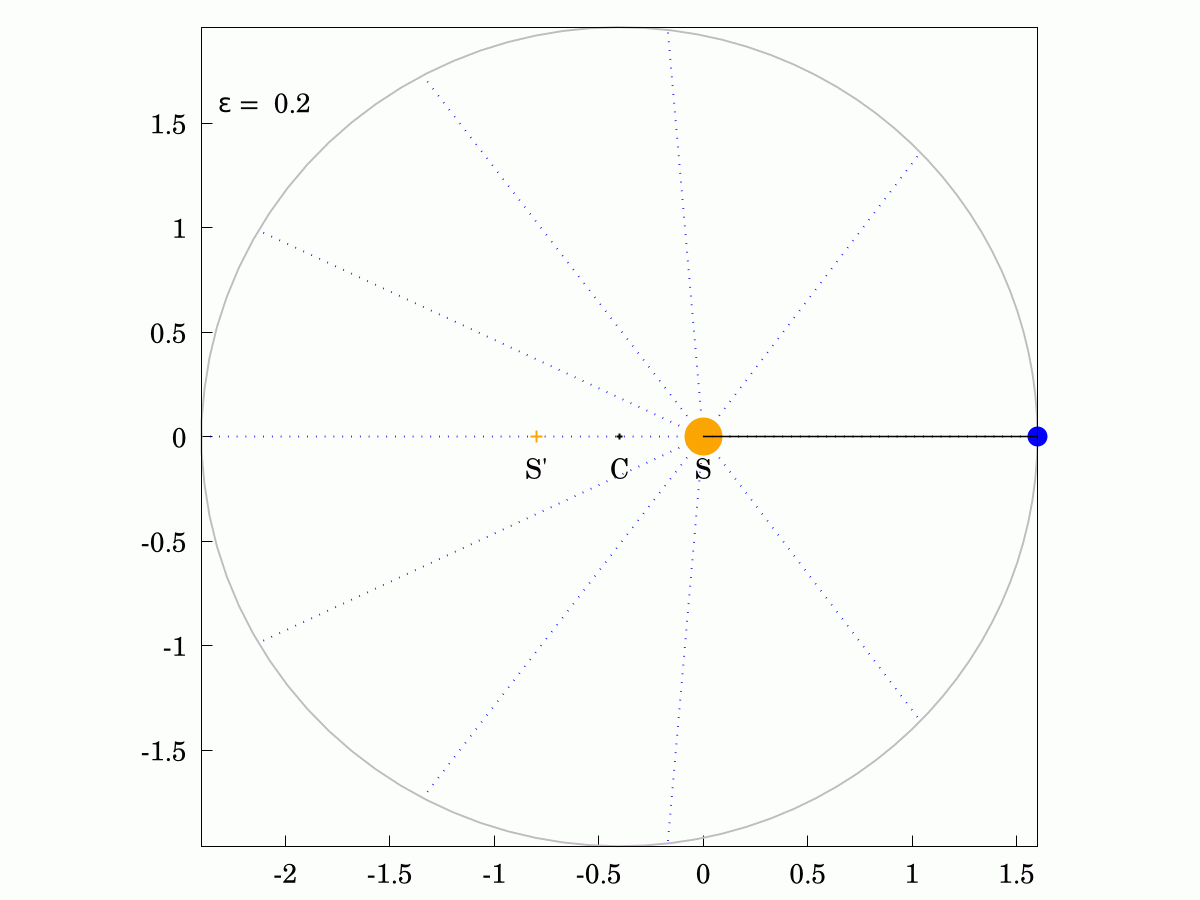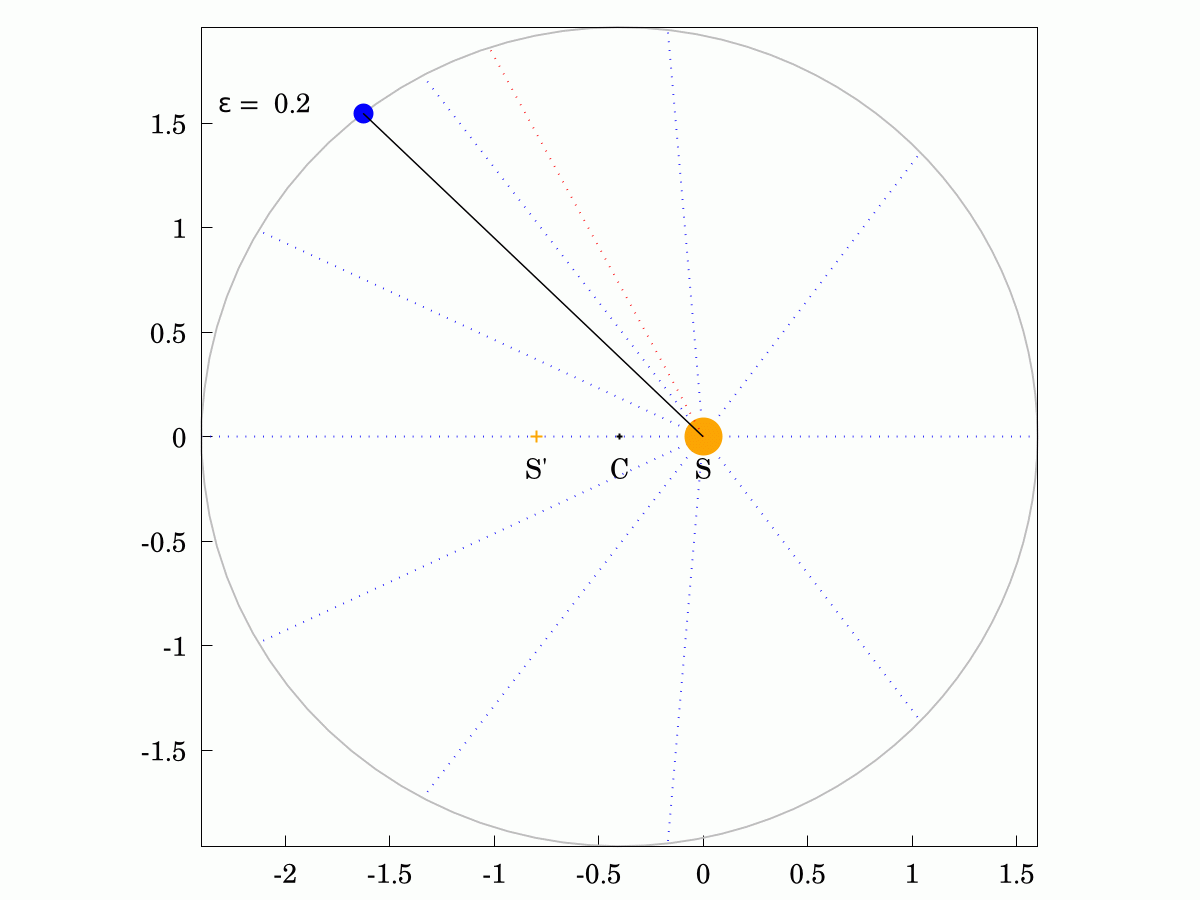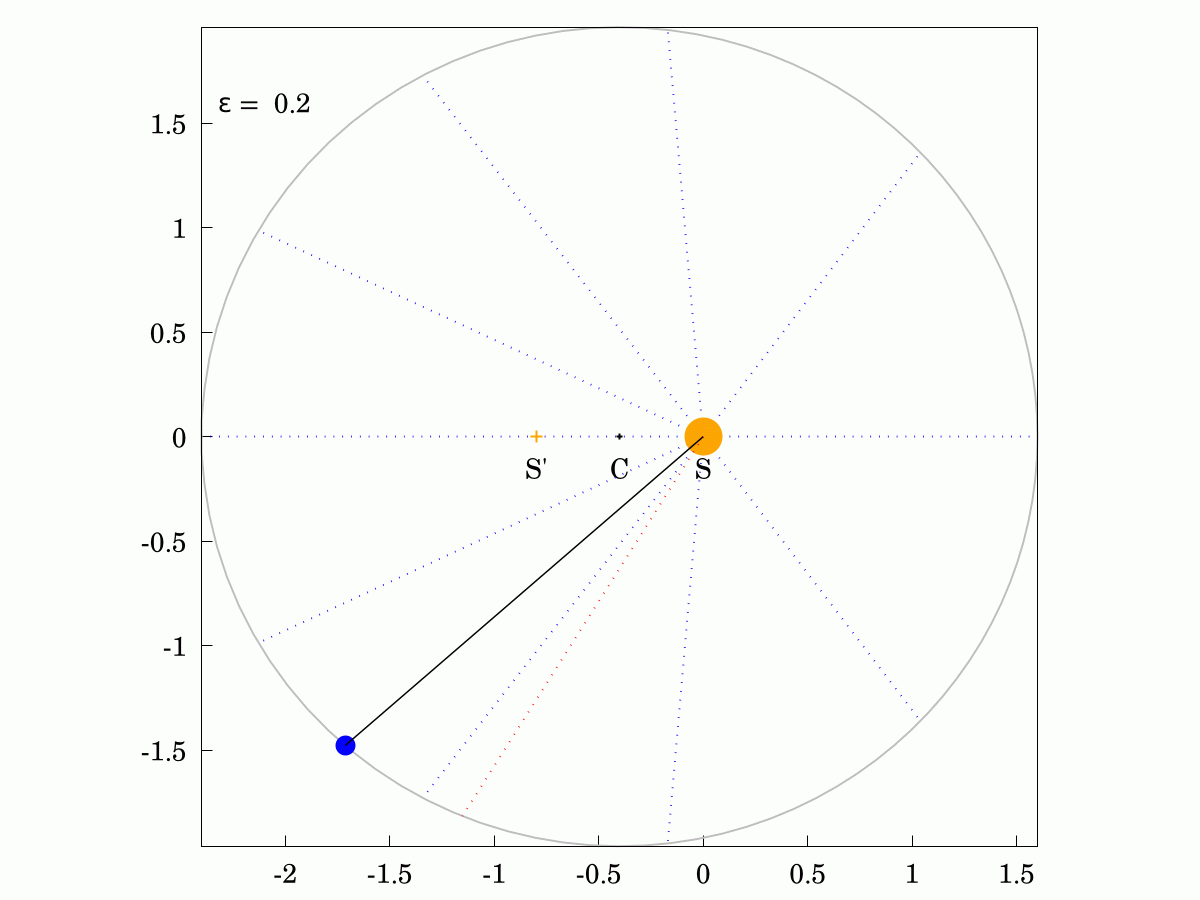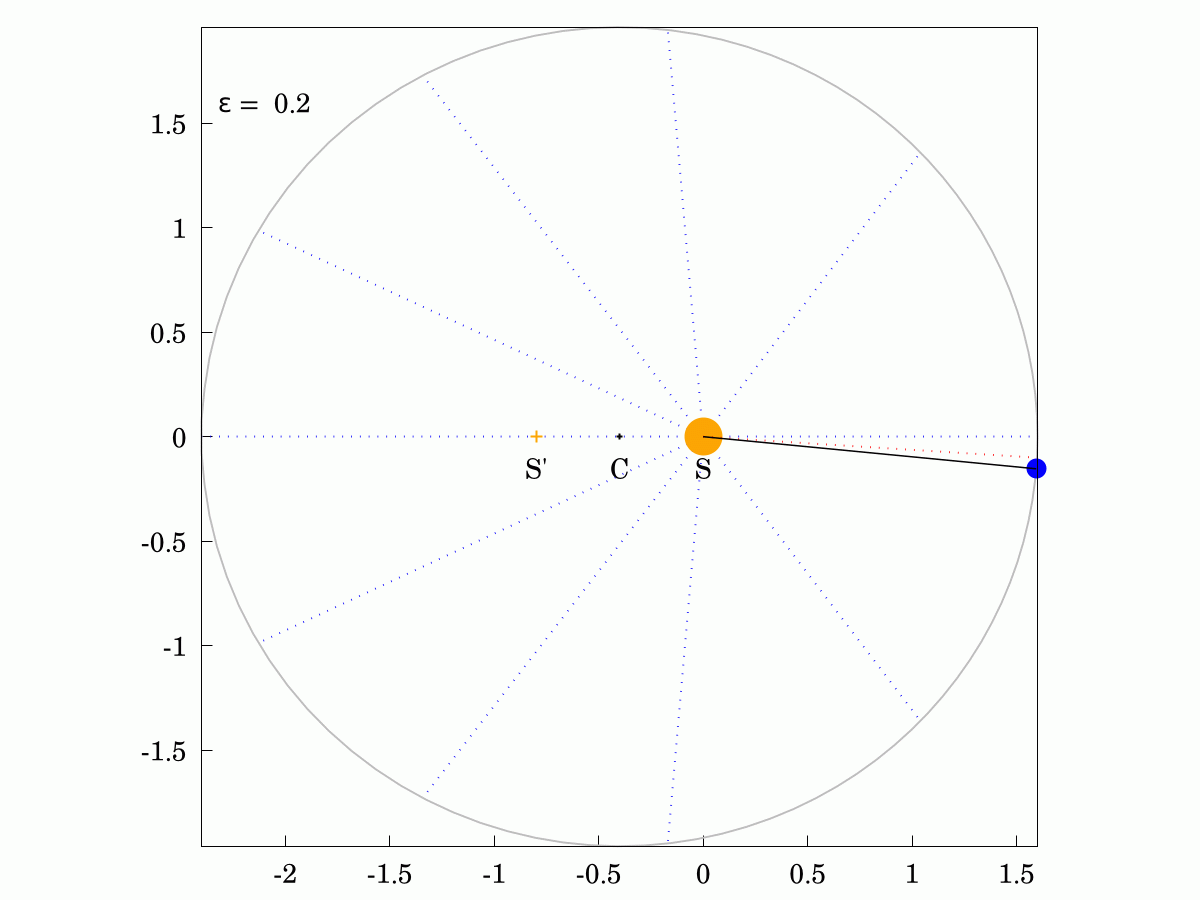
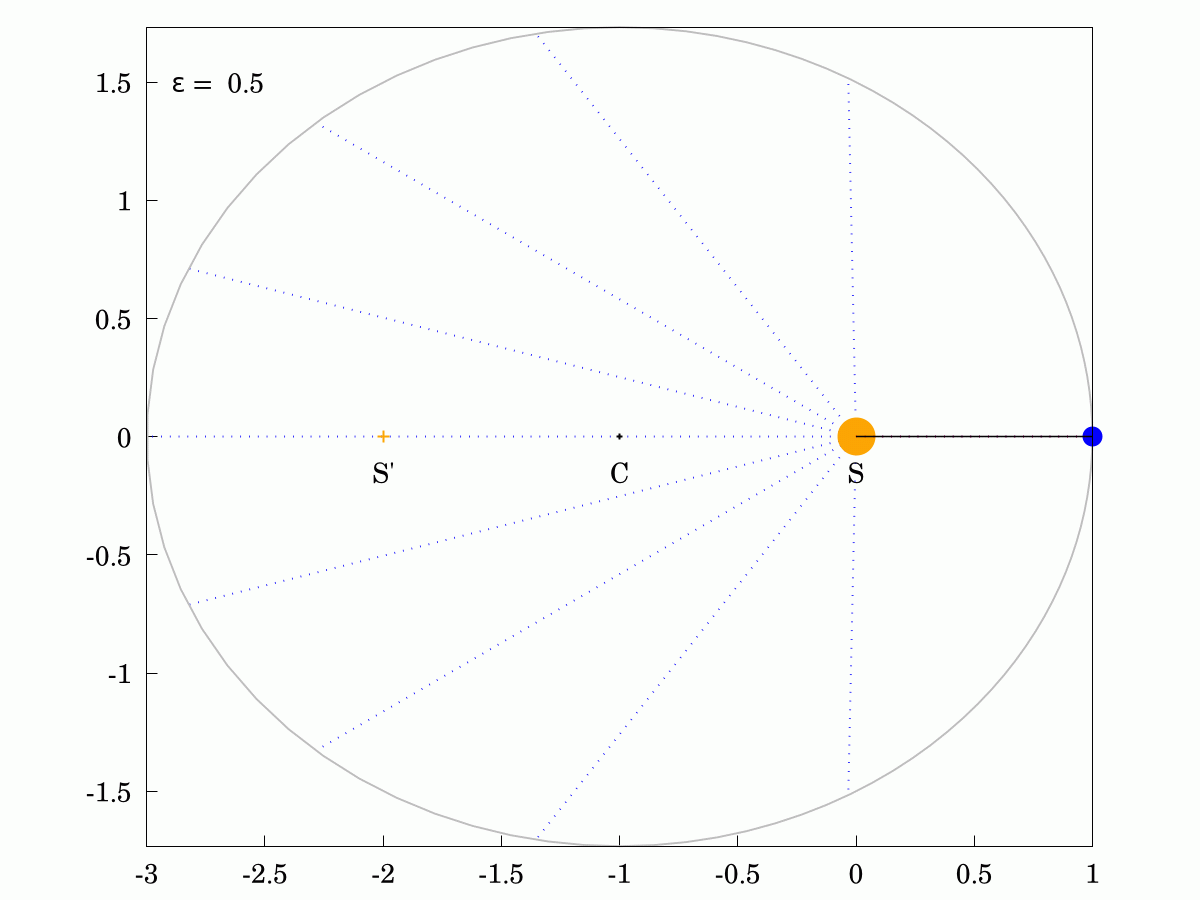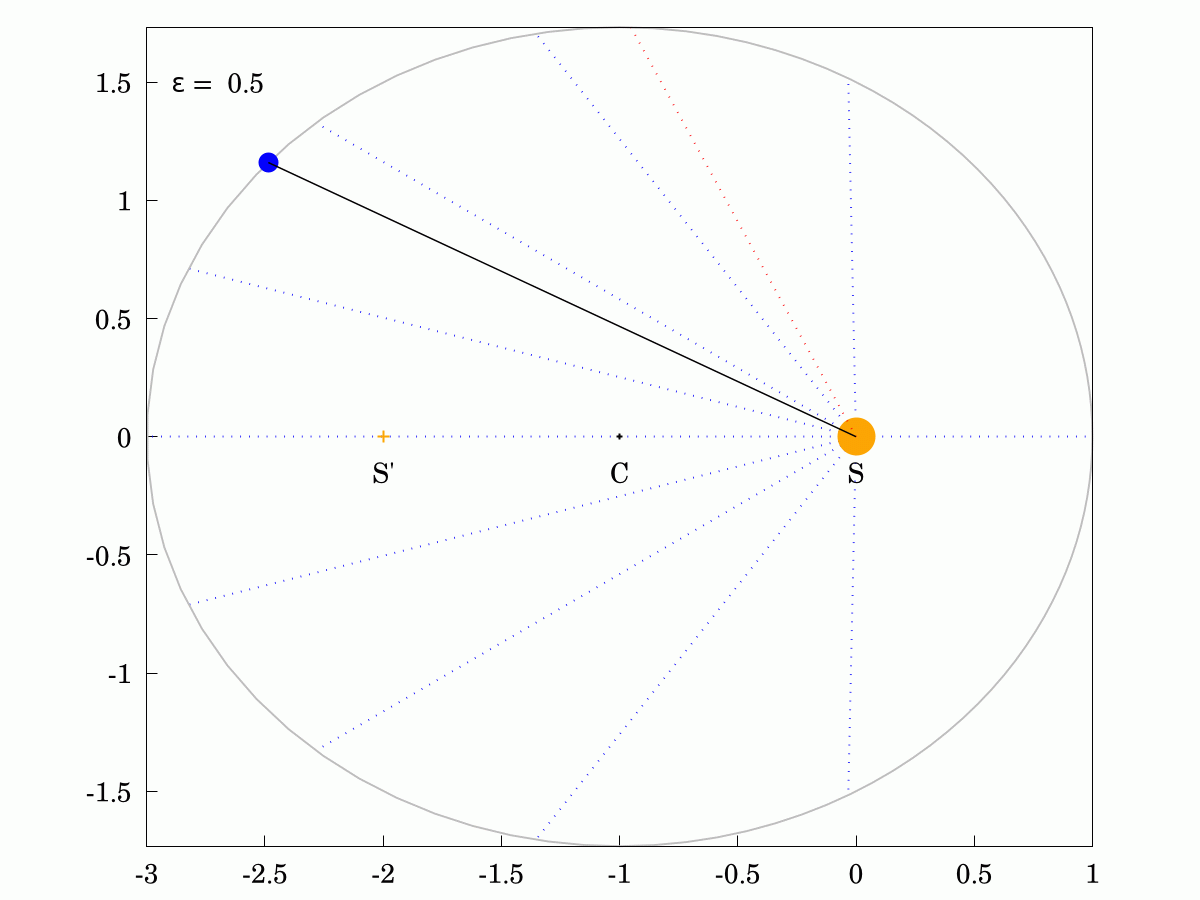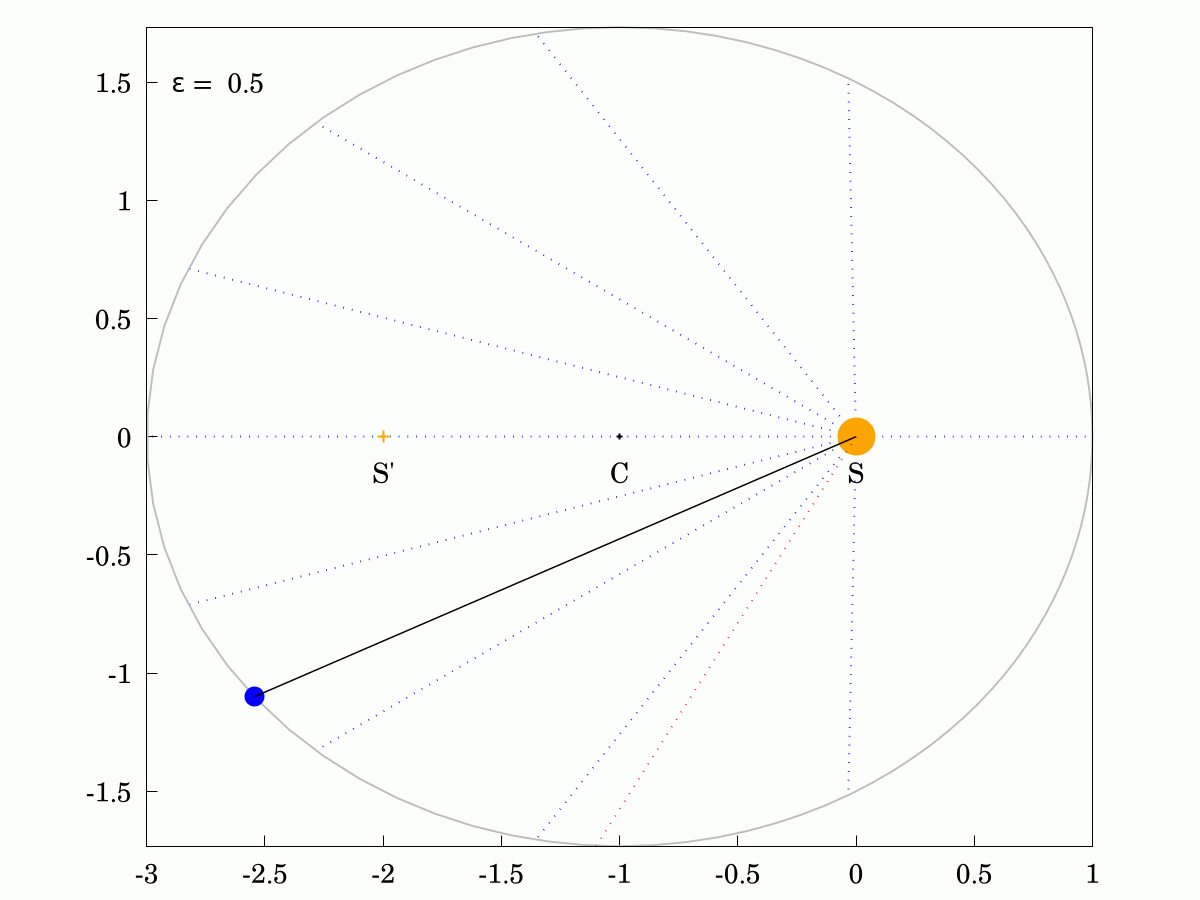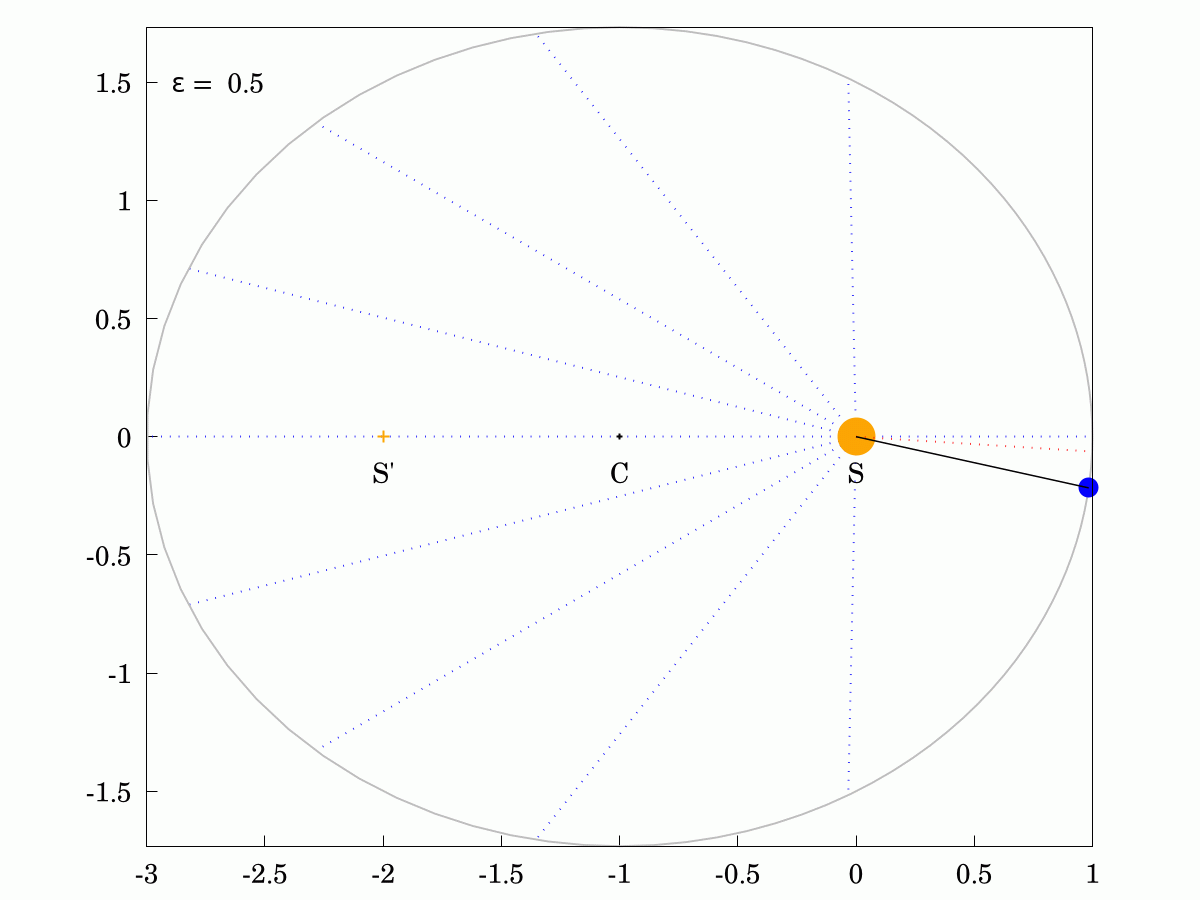
The corollary of this law is that the angular velocity of the planet changes over its orbit, being faster when it is closer to the Sun and slower when it is further away. I have shown the constant-velocity position in red and you can see that it lags behind for half the orbit and leads for the other half.
These animations required me to learn the #mathematics of #CelestialMechanics and I had to find out what terms like #MeanAnomaly, #EccentricAnomaly and #TrueAnomaly are. It also requires the #NumericalSolution of one algebraic equation, which was fun to investigate. All the details are on the #Wikipedia page for Kepler's Laws here:
https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion
The third law relates the orbital period to the mean distance from the Sun but that is not covered here.
#MyWork #Maxima #WxMaxima #FreeSoftware #Physics #Astronomy #AnimatedGif #Animation
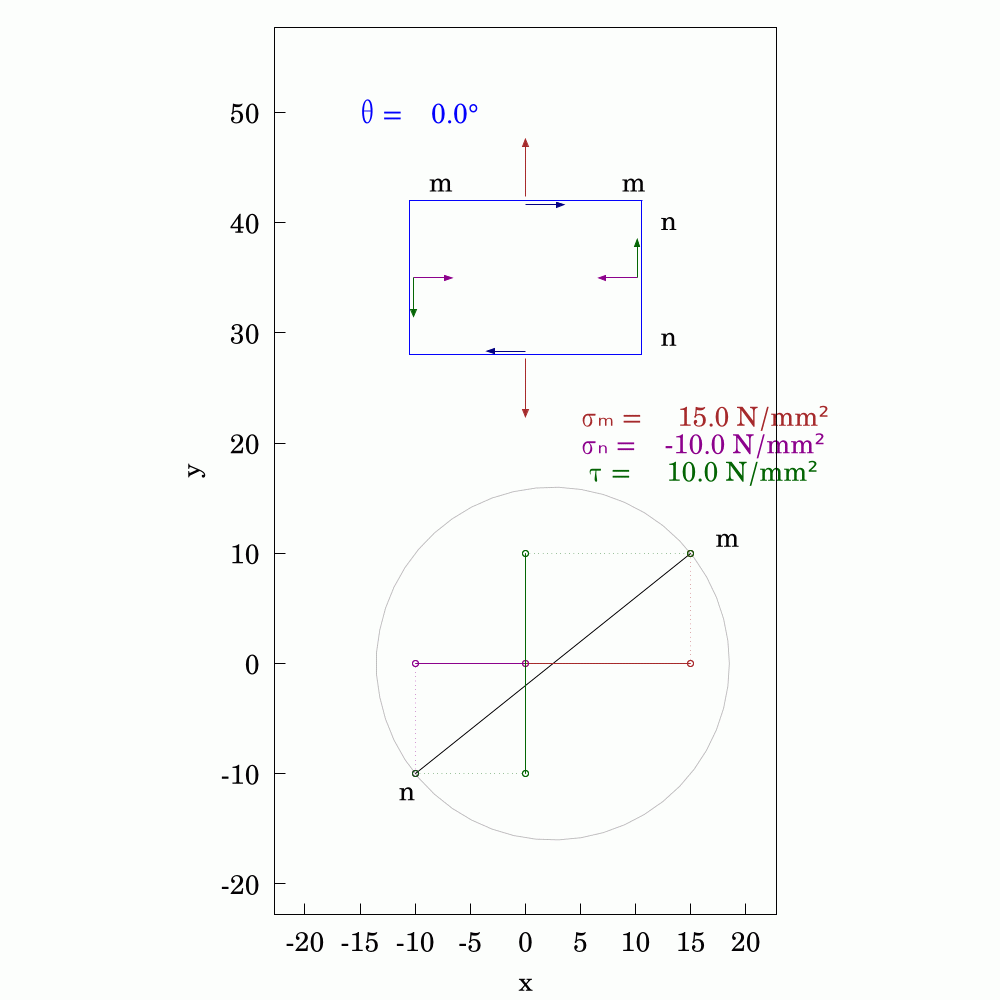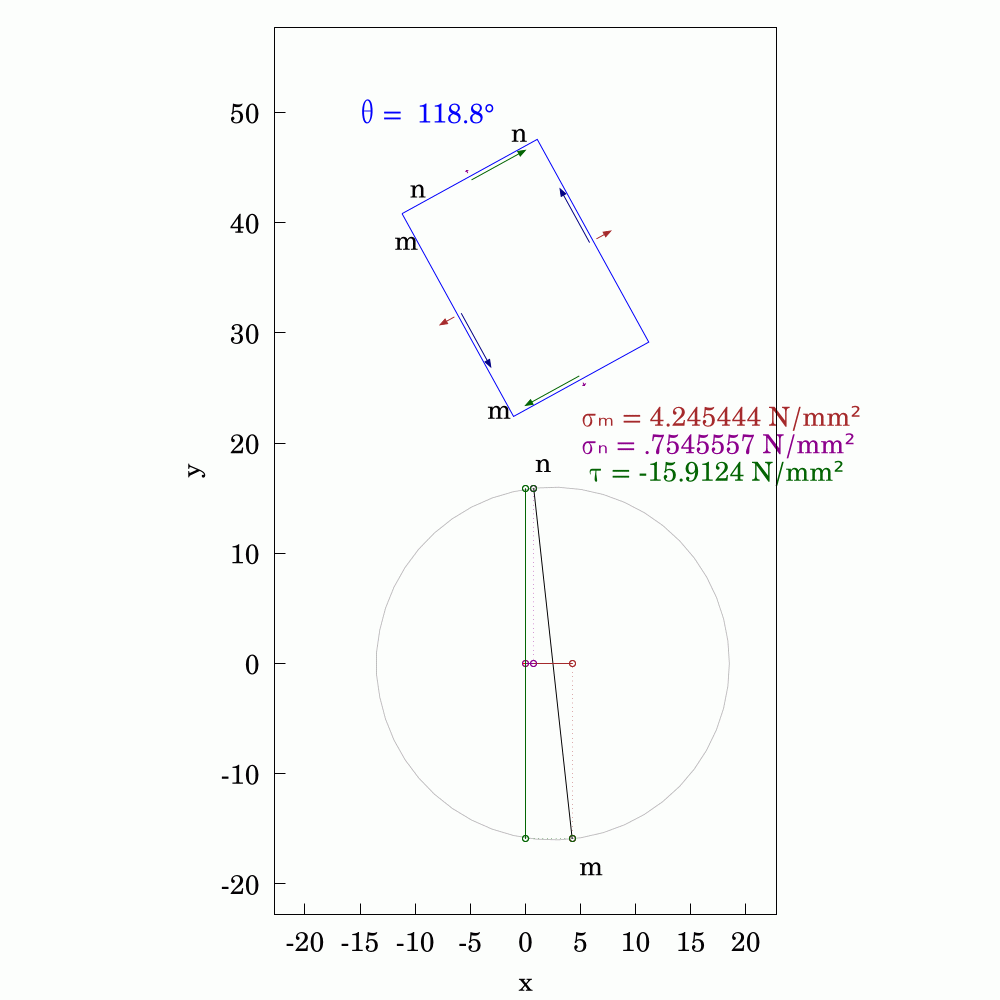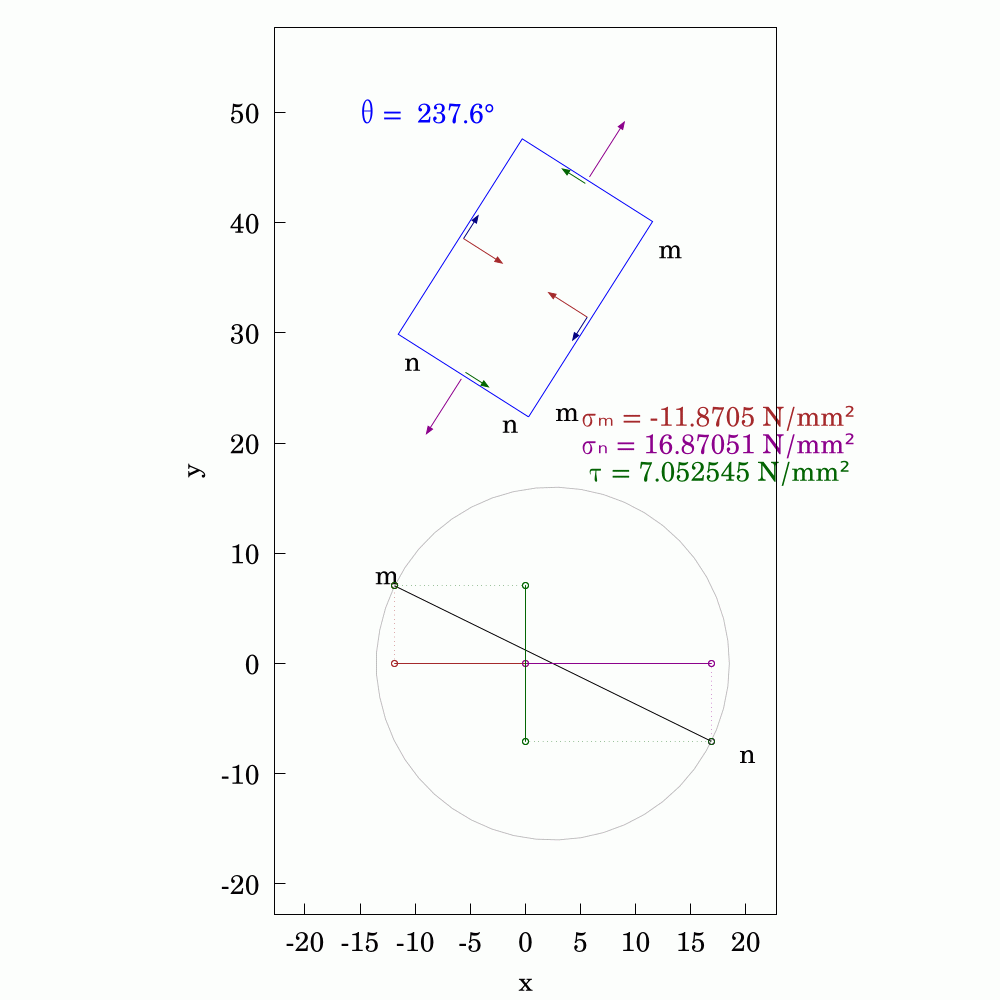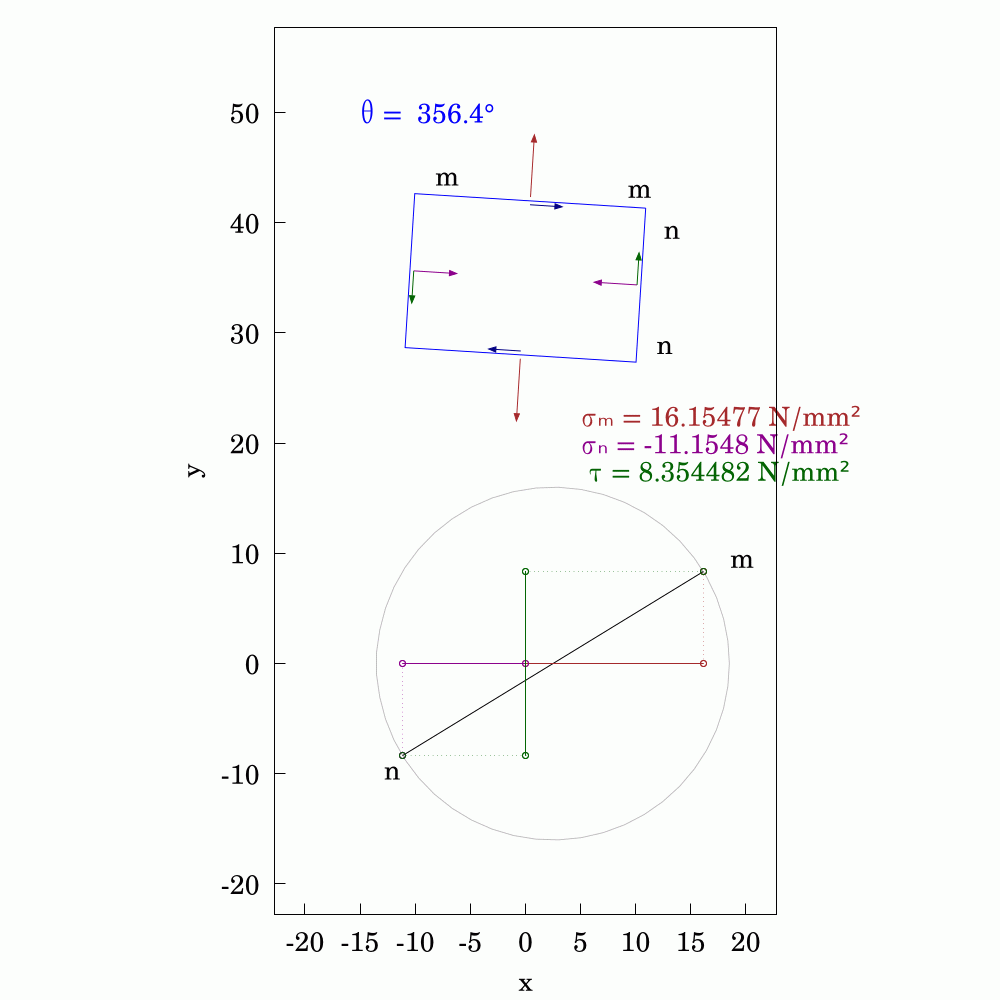
In #SolidMechanics, #stress has some counter-intuitive properties, particularly when you rotate the coordinate system. The values of normal and shear stress transform according to the rules of #second-order #tensors, which is a step above #vectors (first-order tensors). To avoid always having to use #matrix #algebra to find the components, #engineers and #mathematicians have long used the Mohr's circle to evaluate them. This is a very handy tool and allows you to find the new values by using circular geometry instead.
Here, I've used #WxMaxima to create this #animation.
#Mechanics #Mathematics #Engineering #MohrsCircle #FreeSoftware
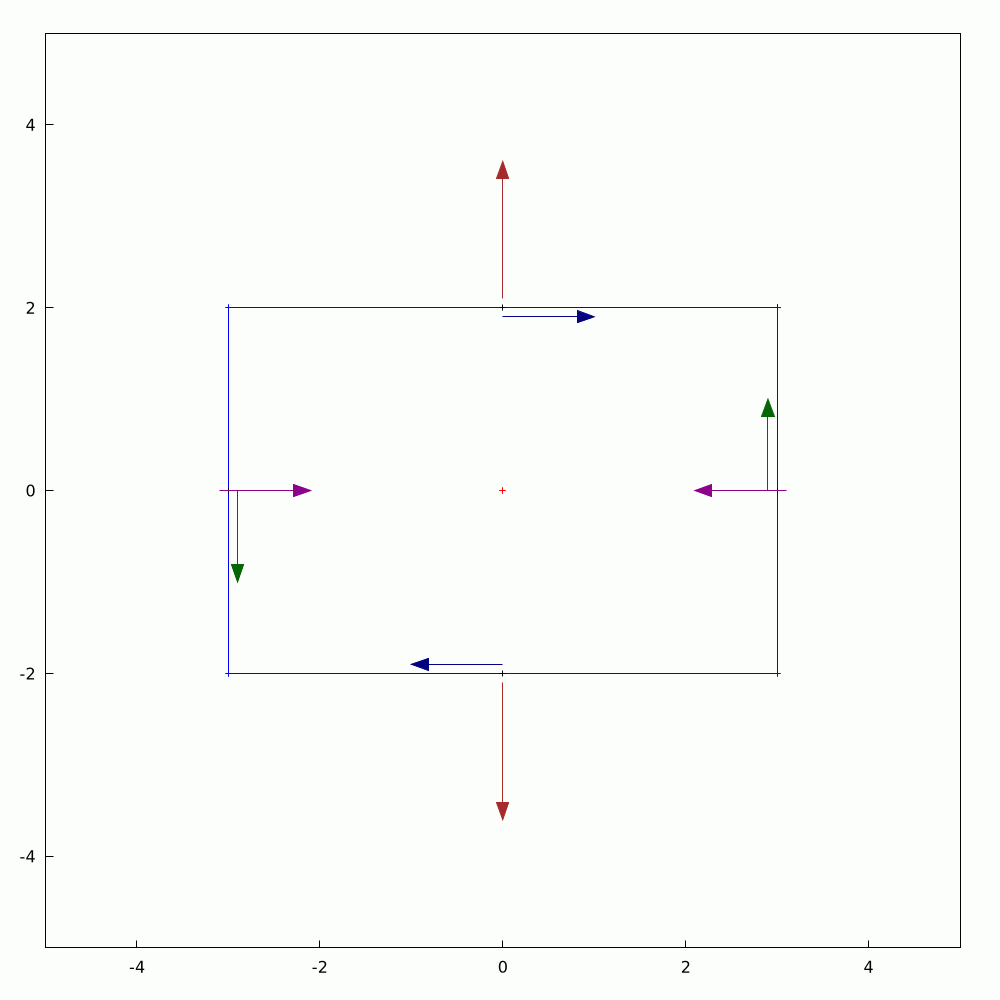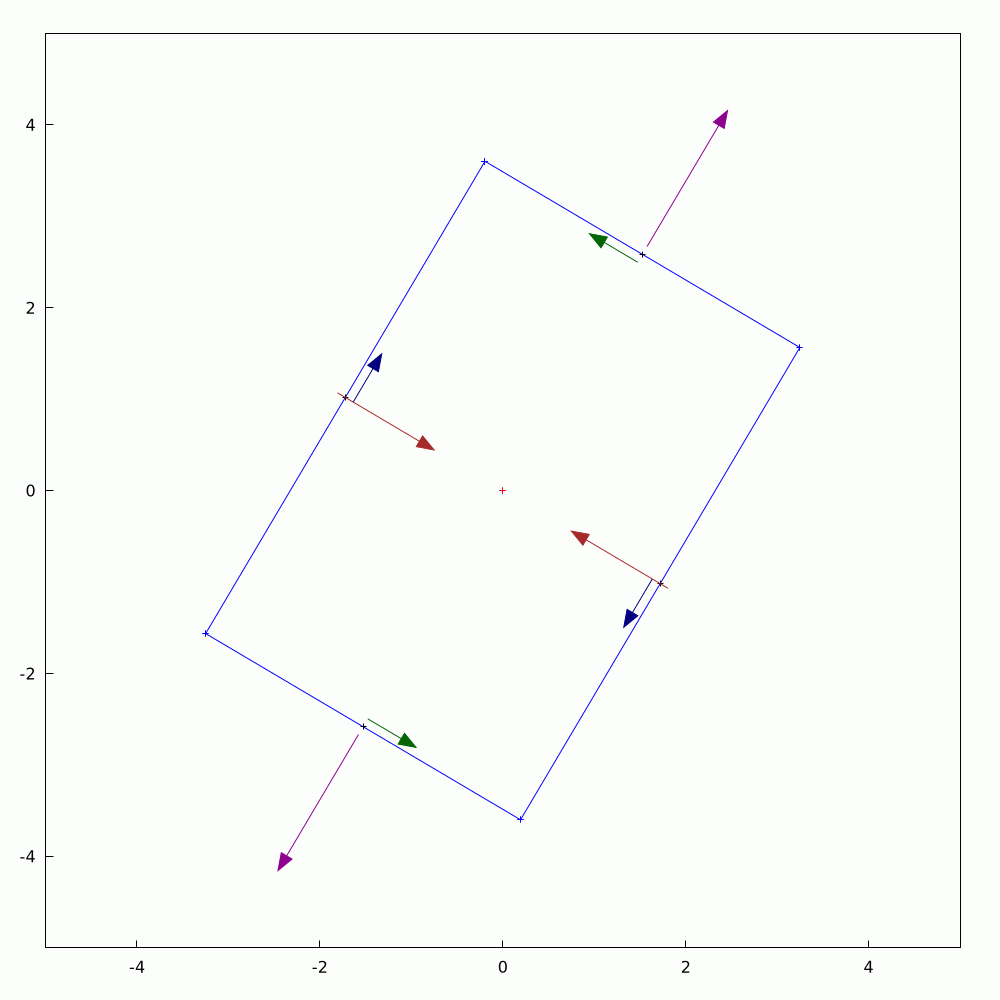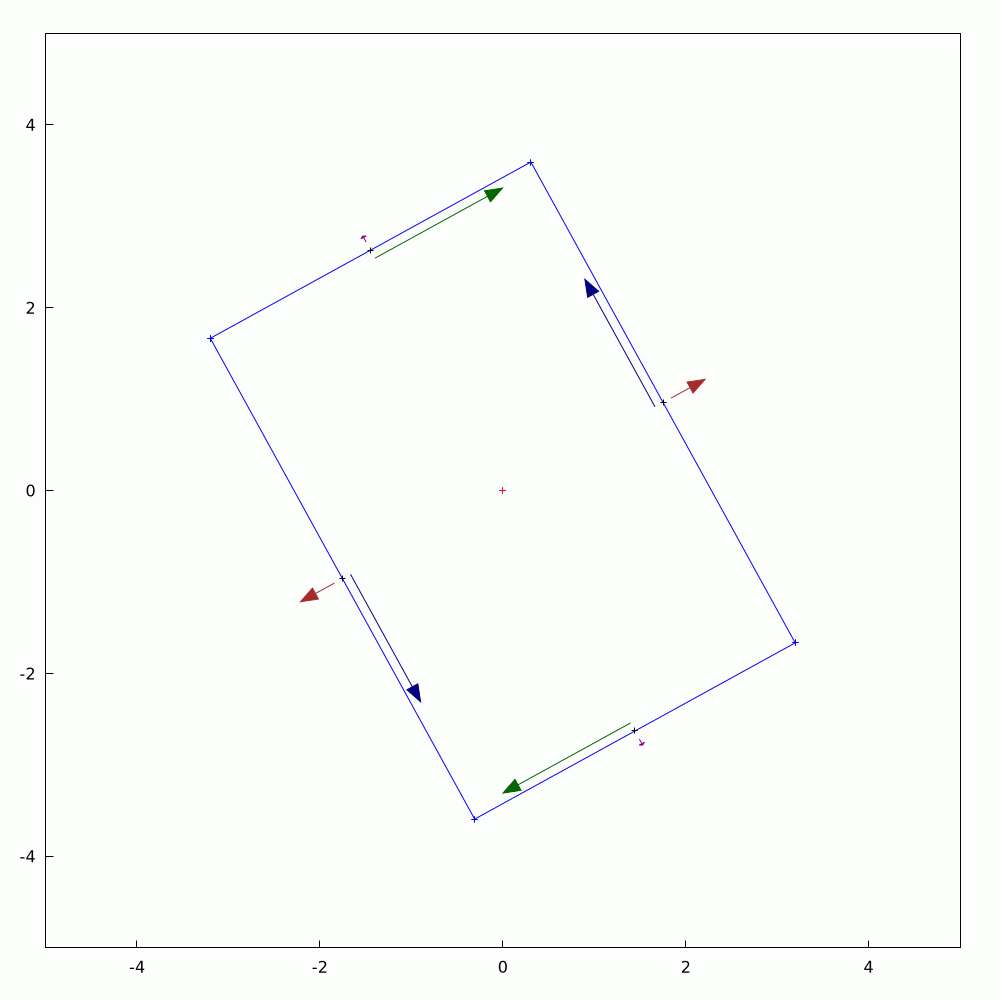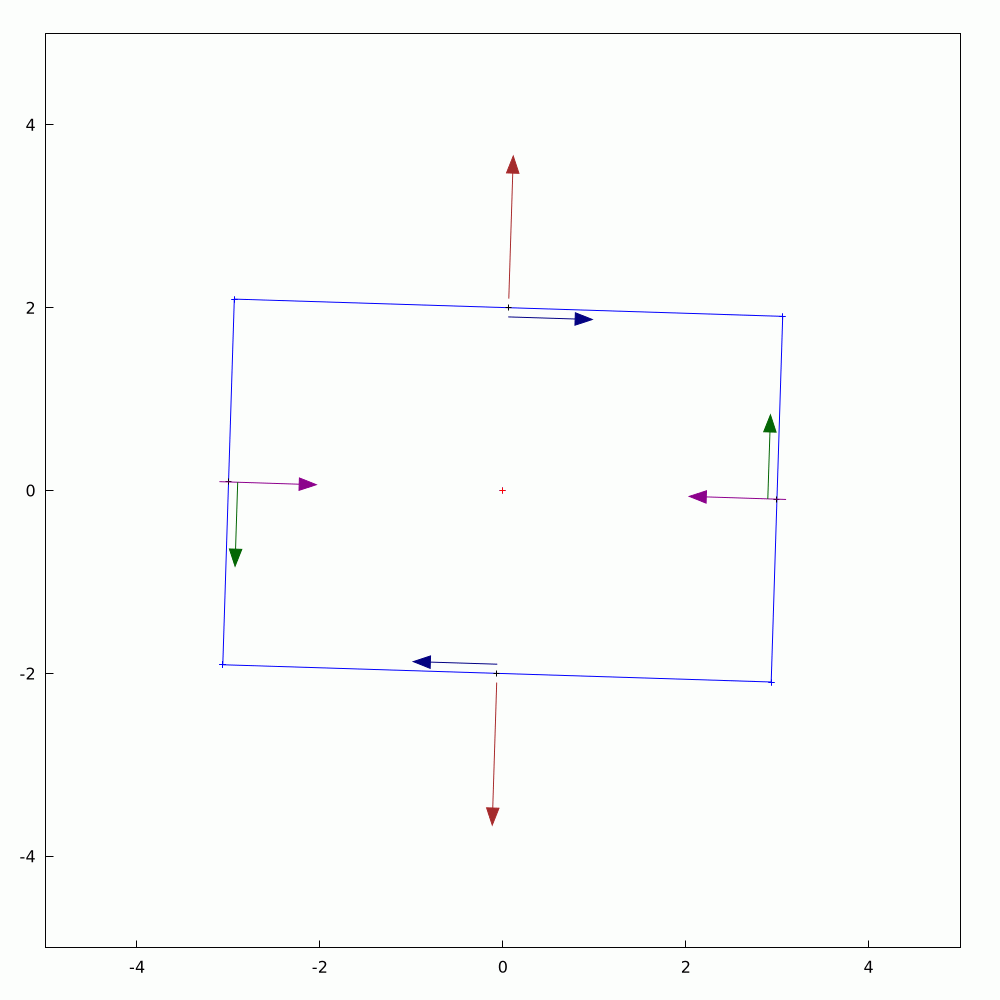
In the #2D #elasticity, #equilibrium of #stresses can be represented on an infinitesimal rectangular element with components of both #DirectStress and #ShearStress generally acting on all four edges. If you were to rotate the rectangle, the stresses change in a precisely orchestrated fashion. In the orientation where the shear stress components vanish, we get what are called #PrincipalStresses and they and their directions can be ascertained precisely through #eigenvalue analysis. This little graphical demonstration shows one example of such a state. The #AnimatedGif was produced a routine written in #WxMaxima.
#Mathematics #TheoryOfElasticity #Mechanics #SolidMechanics #Engineering #MyWork #CCBYSA #WorkInProgress