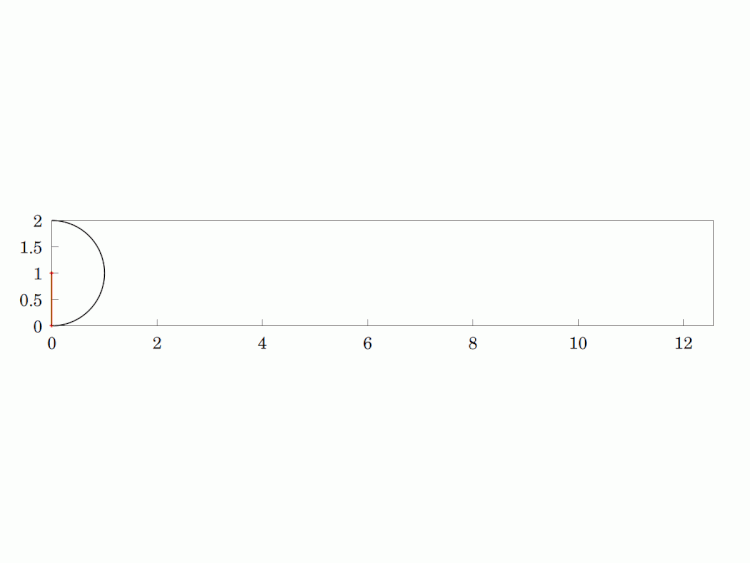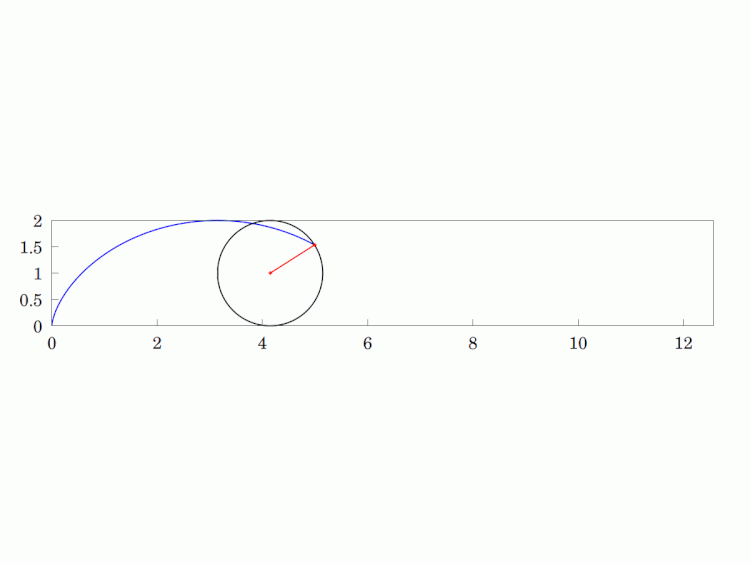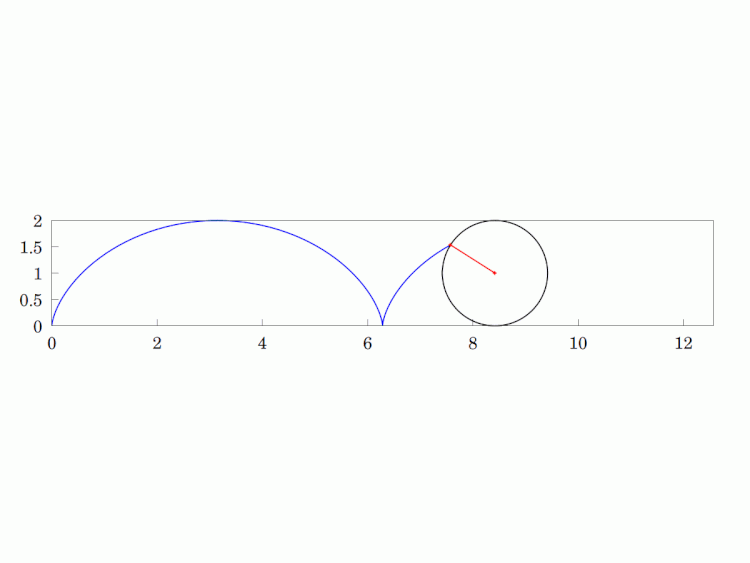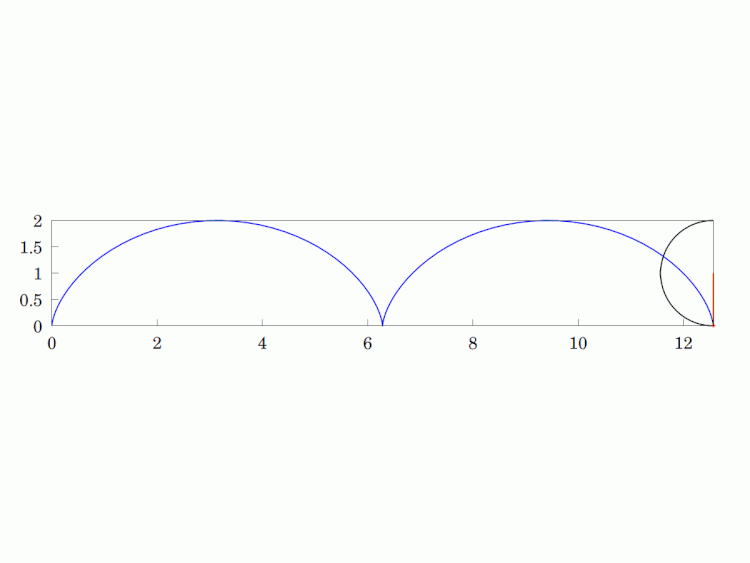
Imagine a circular wheel rolling, without skidding, on a flat, horizontal surface. The #locus of any given point on its #circumference is called a #cycloid. It is a #periodic #curve over a length equivalent to the #circle's circumference and has #cusps whenever the point is in contact with the surface (i.e. the two sides of the curve are tangentially vertical at that point).
Interestingly, it is also the curve that solves the #Brachistochrone problem, which means that starting at a cusp on the inverted curve (maximum height), a frictionless ball will roll under uniform gravity in minimum time from the start to any other point on the curve, even beating the straight line path.
#Mathematics #Geometry #Maths #AppliedMathematics #Mechanics #Kinematics #Dynamics #Physics #MyWork #CCBYSA #WxMaxima