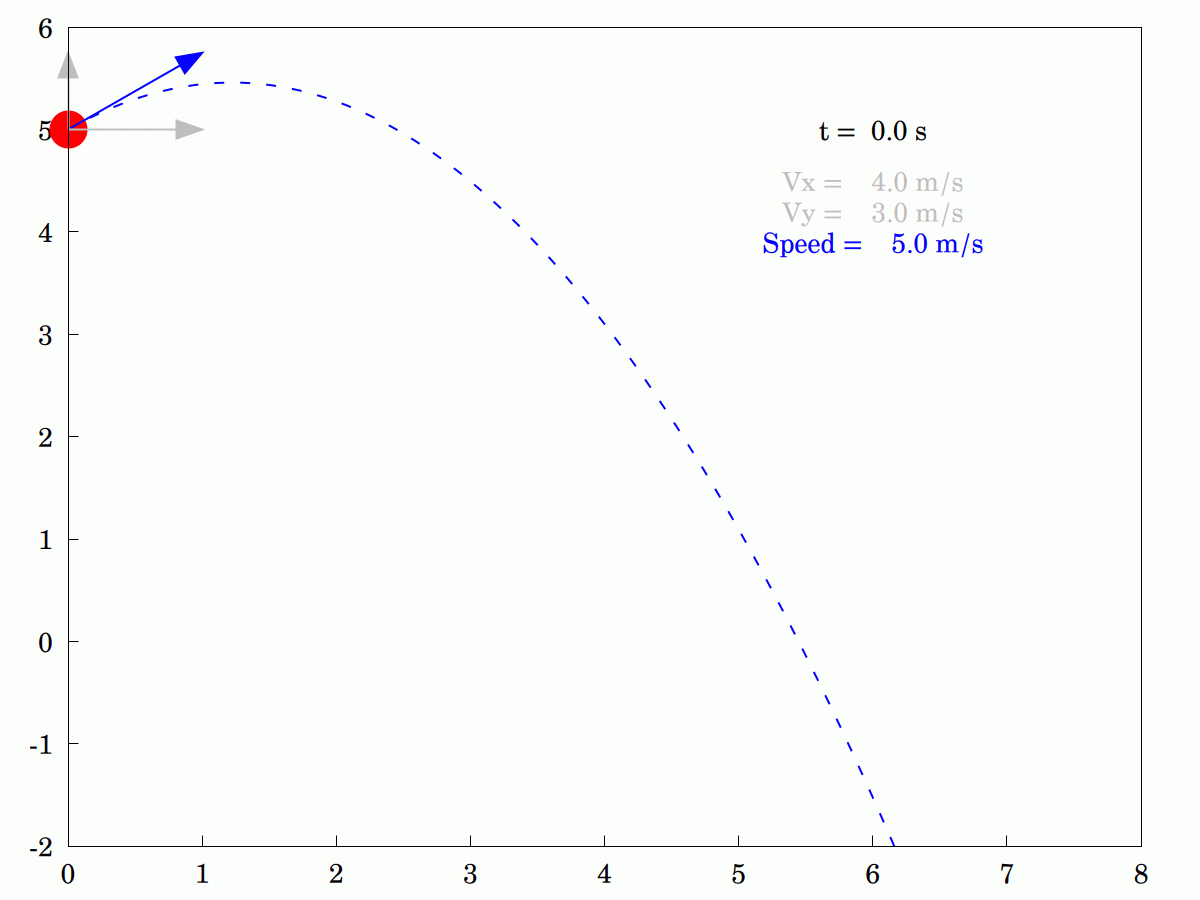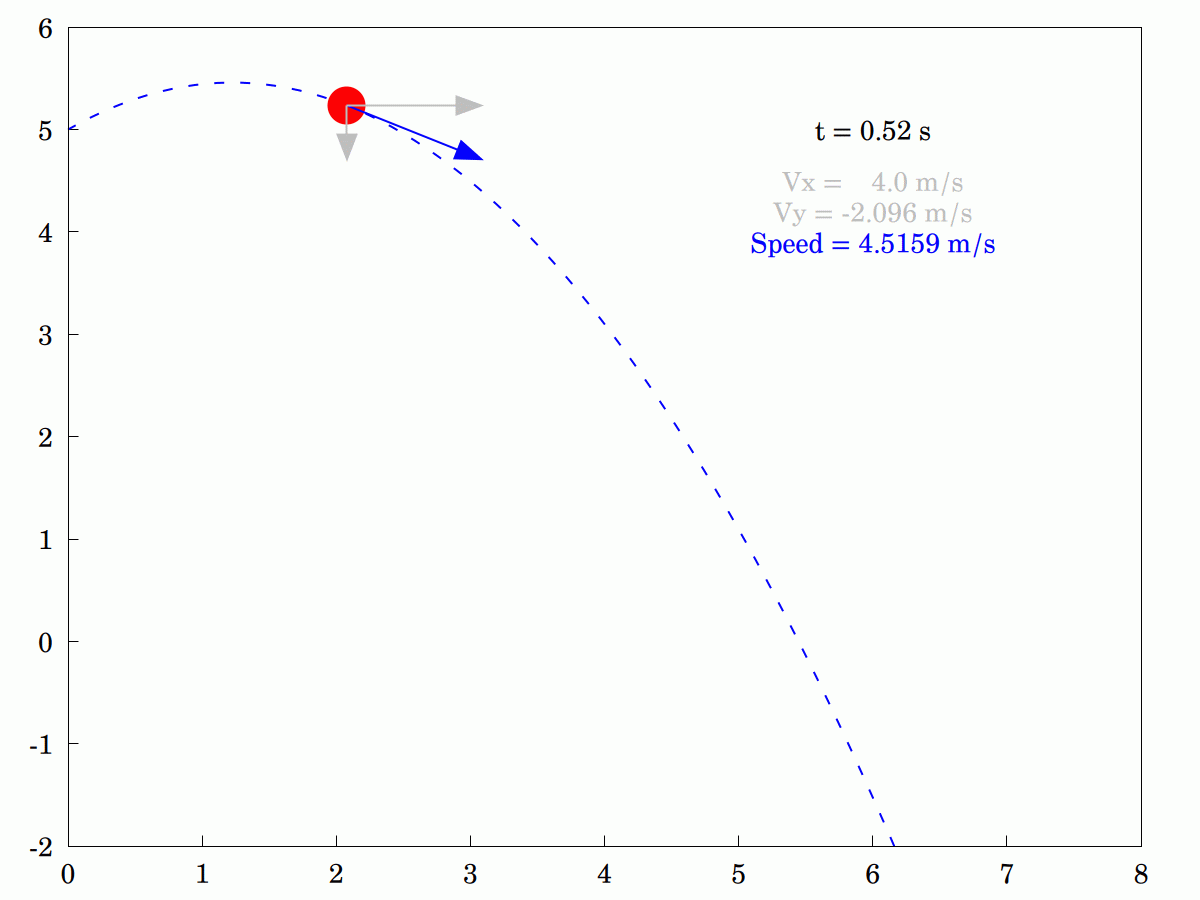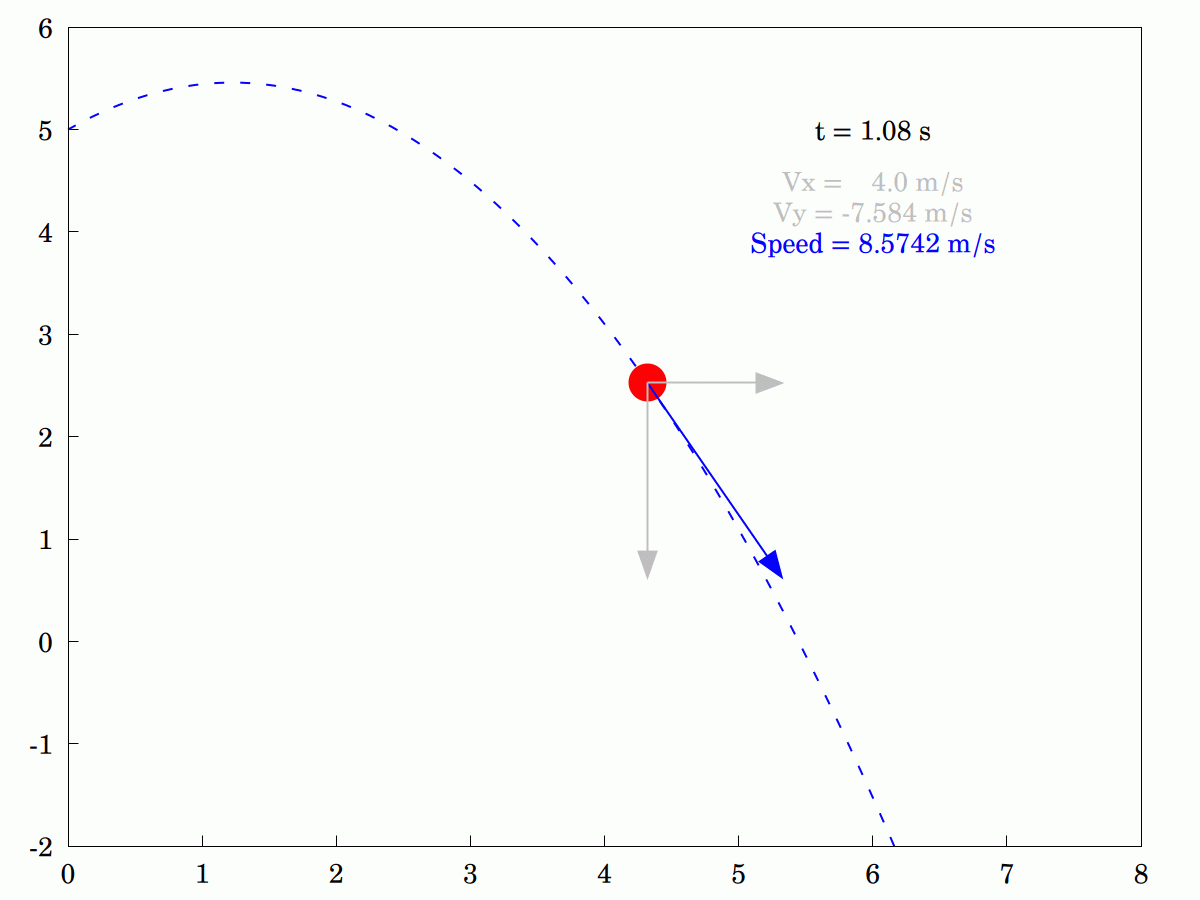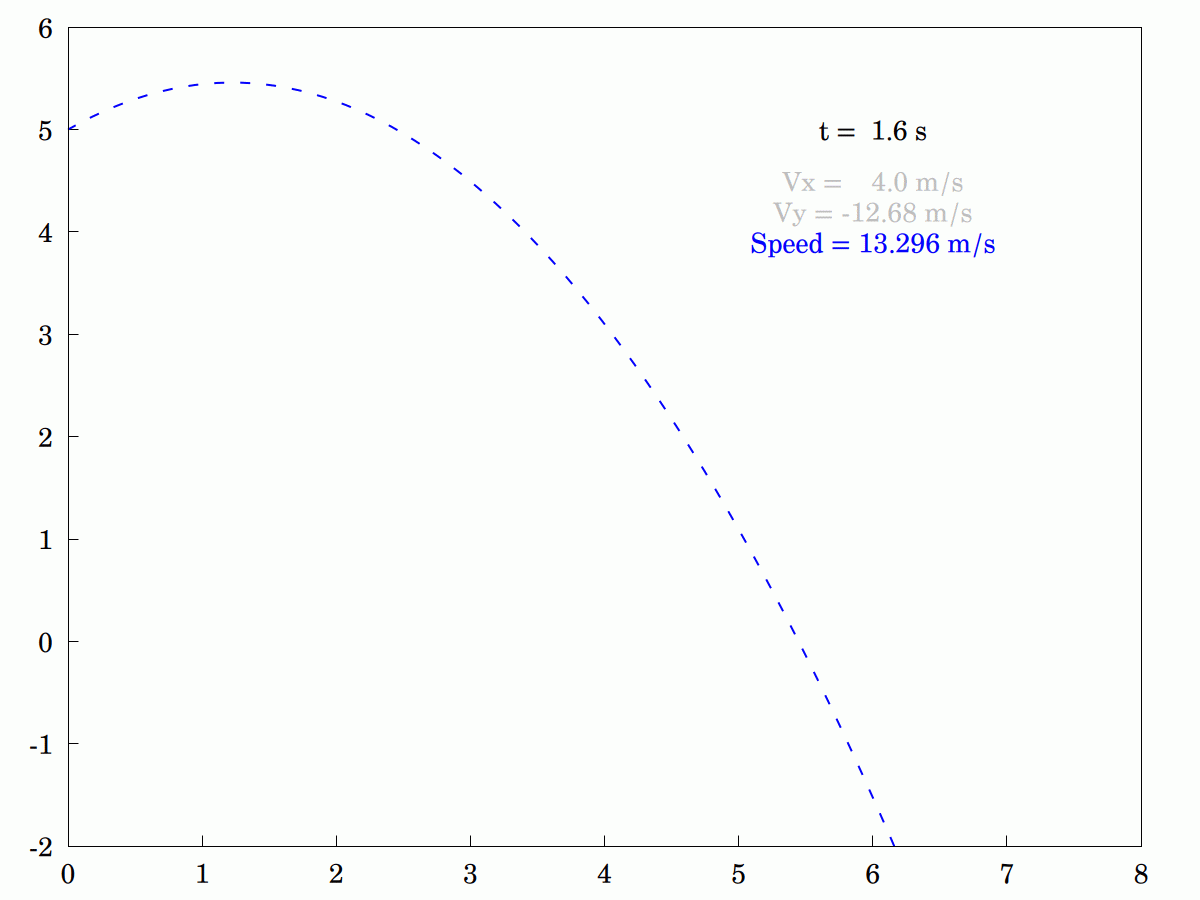
Forgive the recent apparent obsession (I'd call it a fascination) with the #cycloid but I've just discovered something I'd not heard of before. It is also called a #TautochroneCurve or #Isochrone curve, which means that a particle starting from any location on the curve will get to the #MinimumPoint at precisely the same time as a particle starting at any other point.

Here's an #animation I wrote today in #Maxima which illustrates the property.

#Dynamics #Kinematics #Mathematics #AppliedMathematics #Mechanics #ClassicalMecanics #WxMaxima #FreeSoftware #MyWork #CCBYSA

Imagine a circular wheel rolling, without skidding, on a flat, horizontal surface. The #locus of any given point on its #circumference is called a #cycloid. It is a #periodic #curve over a length equivalent to the #circle's circumference and has #cusps whenever the point is in contact with the surface (i.e. the two sides of the curve are tangentially vertical at that point).

Interestingly, it is also the curve that solves the #Brachistochrone problem, which means that starting at a cusp on the inverted curve (maximum height), a frictionless ball will roll under uniform gravity in minimum time from the start to any other point on the curve, even beating the straight line path.

#Mathematics #Geometry #Maths #AppliedMathematics #Mechanics #Kinematics #Dynamics #Physics #MyWork #CCBYSA #WxMaxima

I was explaining to my wife how the #velocity #components of an idealized #projectile differ. She was having some problems understanding that only the #vertical component changes and that the #horizontal component remains constant. In the end, I knocked up this little animation to tr and explain pictorially (the program in #WxMaxima is actually interactive. so you can stop it, step through it or run it backwards if that helps).

#Maths #Mathematics #Mechanics #ConstantAcceleration #Vectors #Dynamics #MyWork #CCBYSA #FreeSoftware