#projectile
A few weeks ago, I posted an example of a #projectile #trajectory in a uniform #GravitationalField without #AirResistance. It's a school-level exercise but it was nice to produce an #animation for it. To model air resistance is a bit more tricky as any #fluid, including #air, is complex and does not necessarily behave as you might expect. A simple model for it might be to assume it is a #linear #viscous fluid offering resistance proportional to the velocity of the projectile, i.e. R = -k.v, where v is the velocity vector and k is a constant which dictates how viscous the fluid is.
Happily, this model has exact solutions so I didn't need to do any numerical integration to find the form of the displacement. Here are four different cases, including the "ideal" case k = 0. The others are k = 0.1, 1 and 10, with the middle one highlighted. The essential difference between the non-resistance case and the others is that horizontal velocity steadily decreases with time and decays towards zero exponentially. The vertical velocity is also reduced but still grows. The most viscous case (k = 10) shows terminal velocity behaviour very quickly and the projectile appears to be moving through treacle.
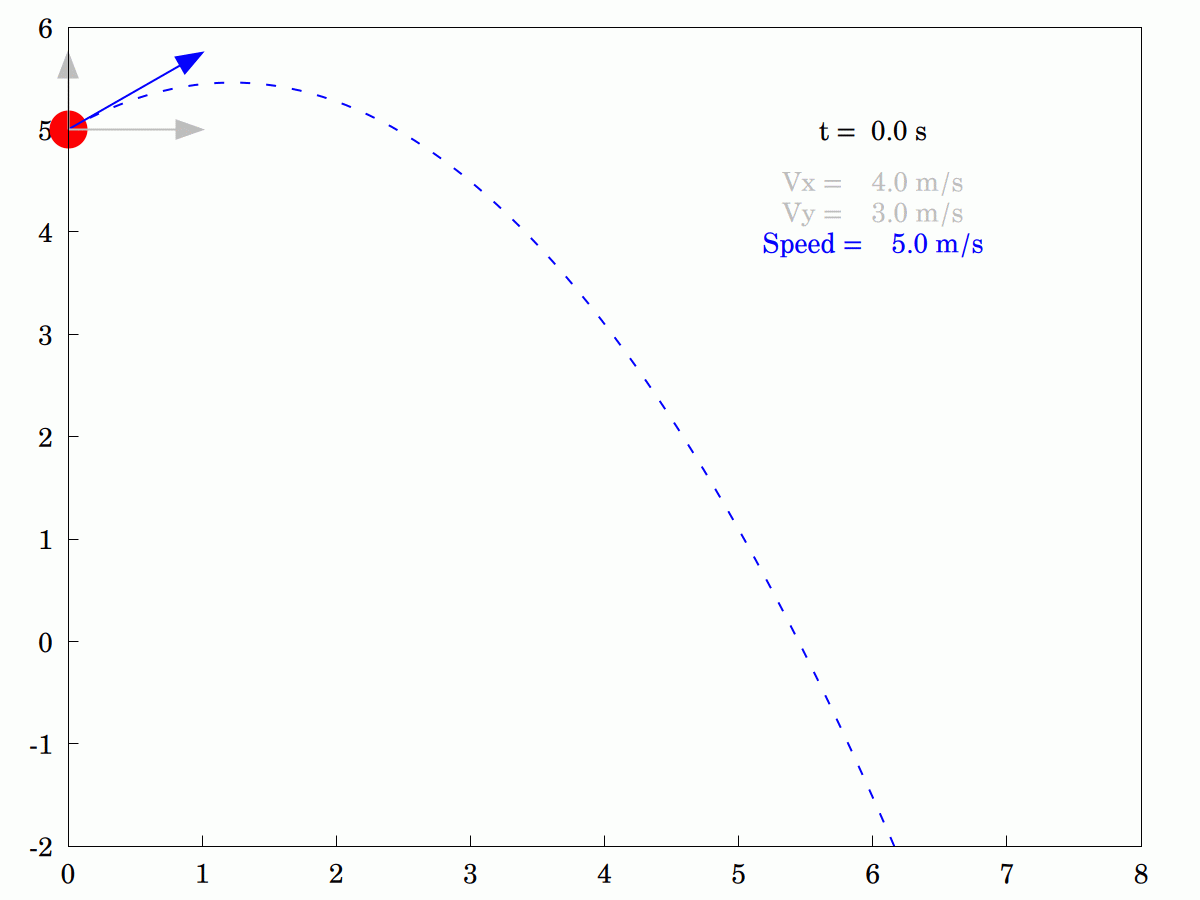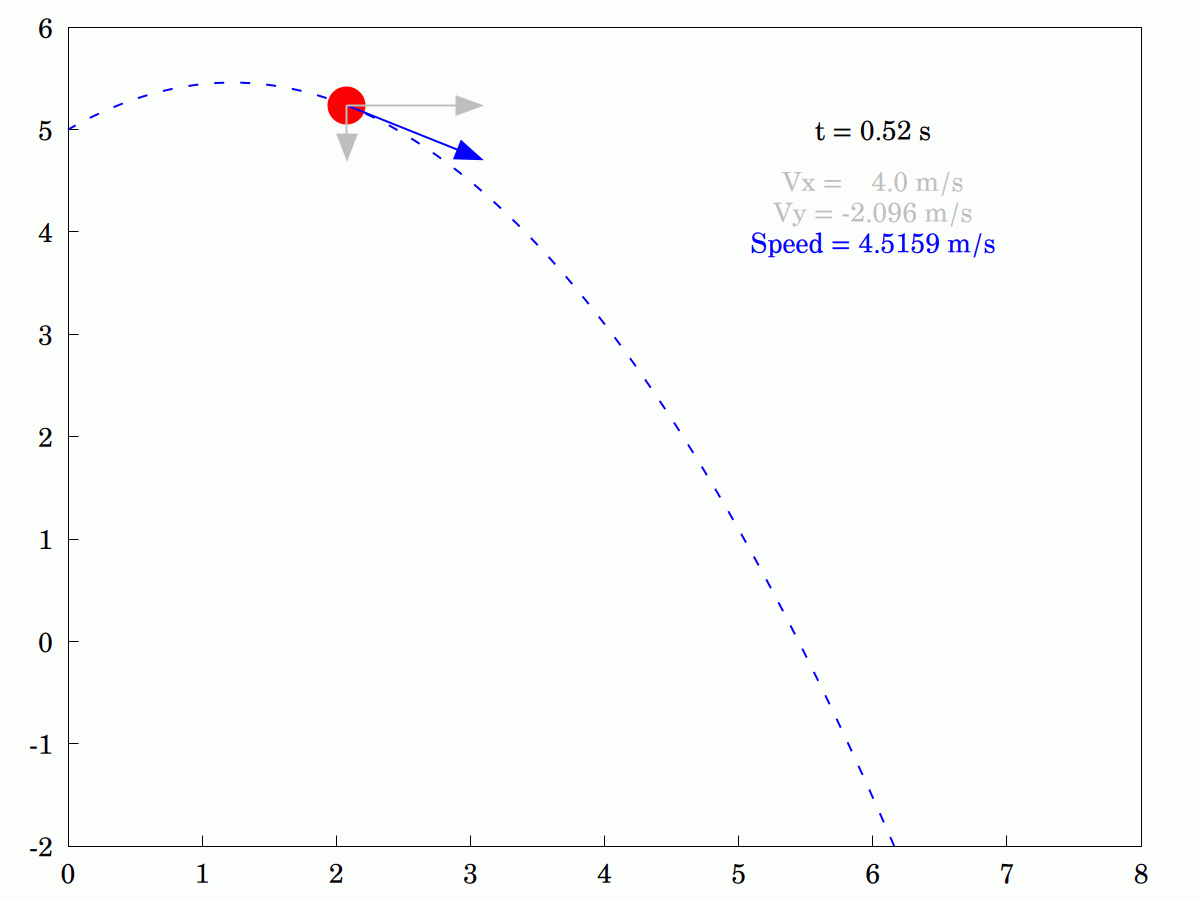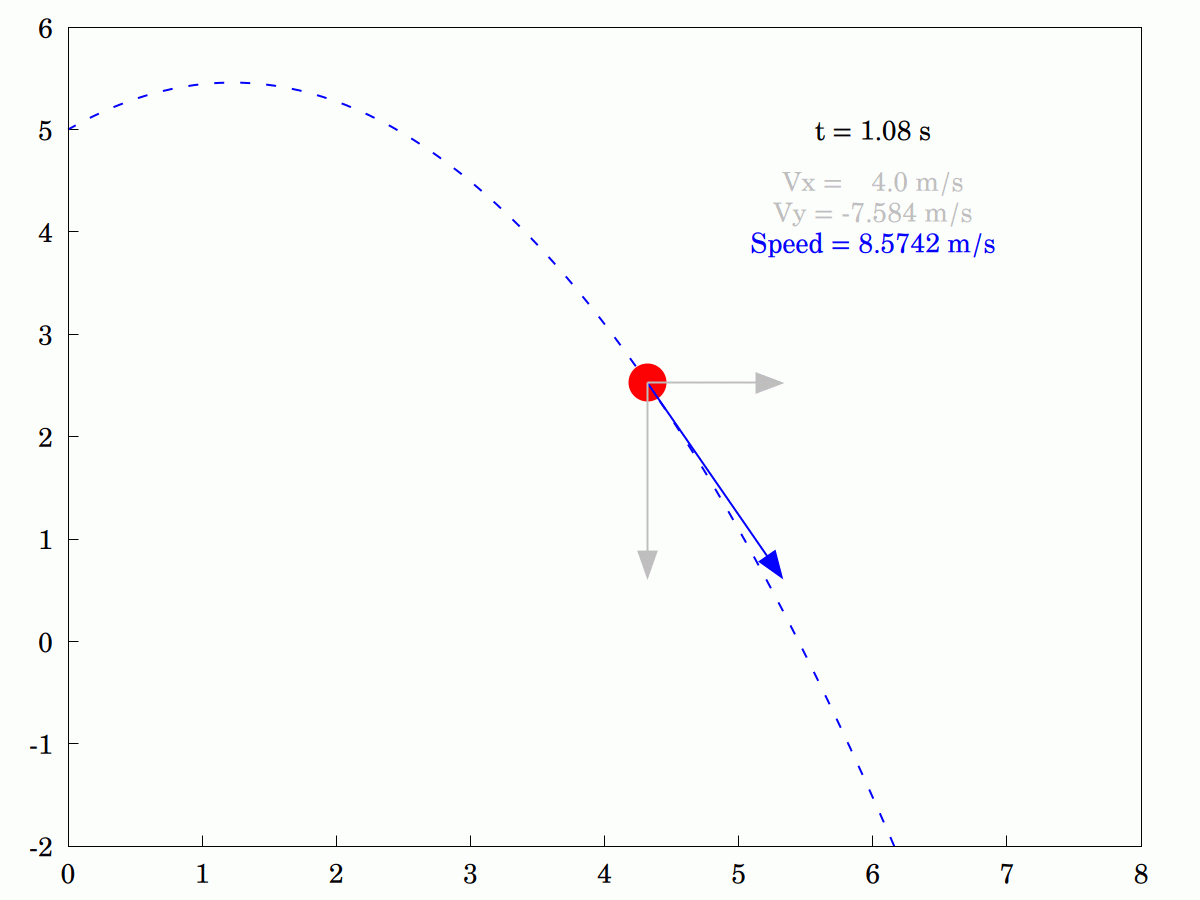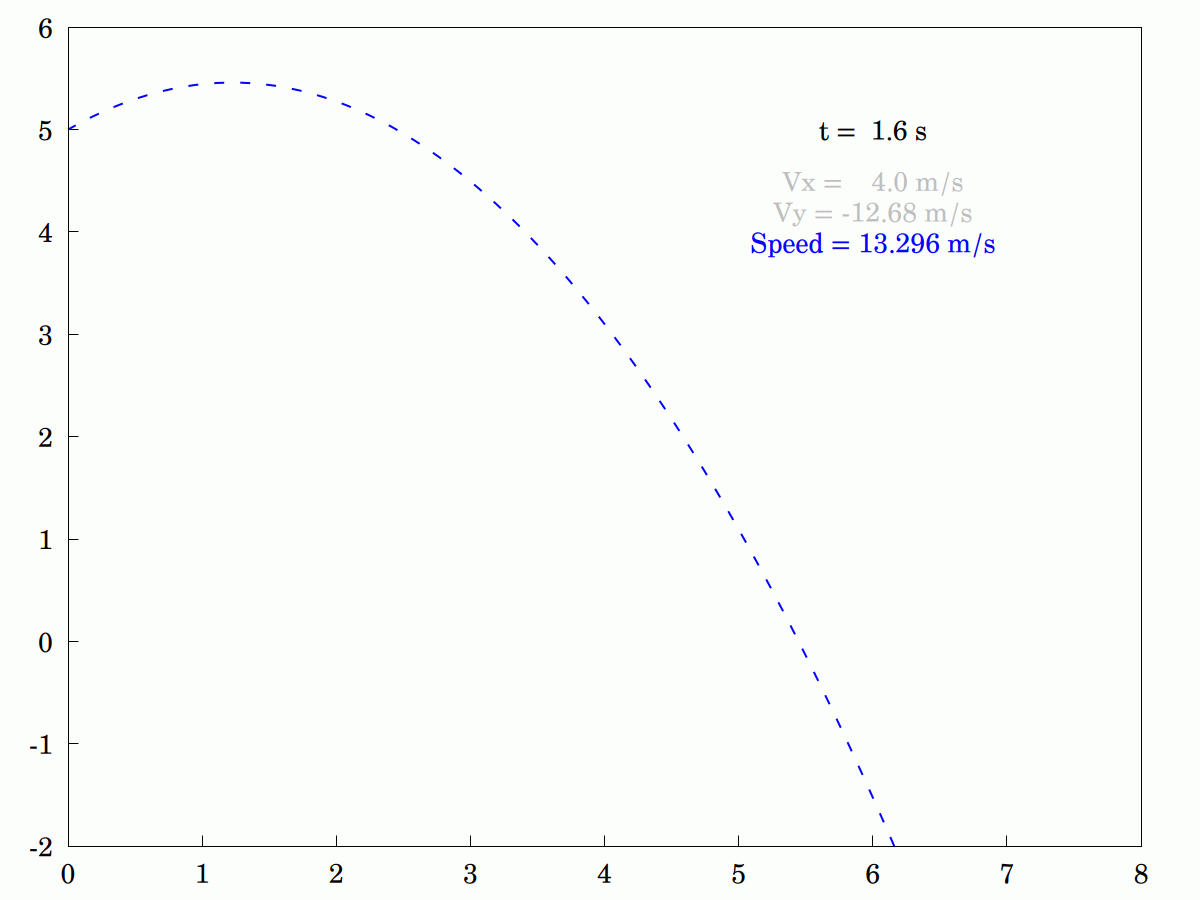
I was explaining to my wife how the #velocity #components of an idealized #projectile differ. She was having some problems understanding that only the #vertical component changes and that the #horizontal component remains constant. In the end, I knocked up this little animation to tr and explain pictorially (the program in #WxMaxima is actually interactive. so you can stop it, step through it or run it backwards if that helps).
#Maths #Mathematics #Mechanics #ConstantAcceleration #Vectors #Dynamics #MyWork #CCBYSA #FreeSoftware