https://www.bitchute.com/video/f6KCXvf24yKM/
FRACTALS, DNA, GOLDEN RATIO, THE STORY OF BLISS - DAN WINTER
#Fractals, #DNA, #Golden #Ratio, The #Story #of #BLISS - #DanWinter
#fractals
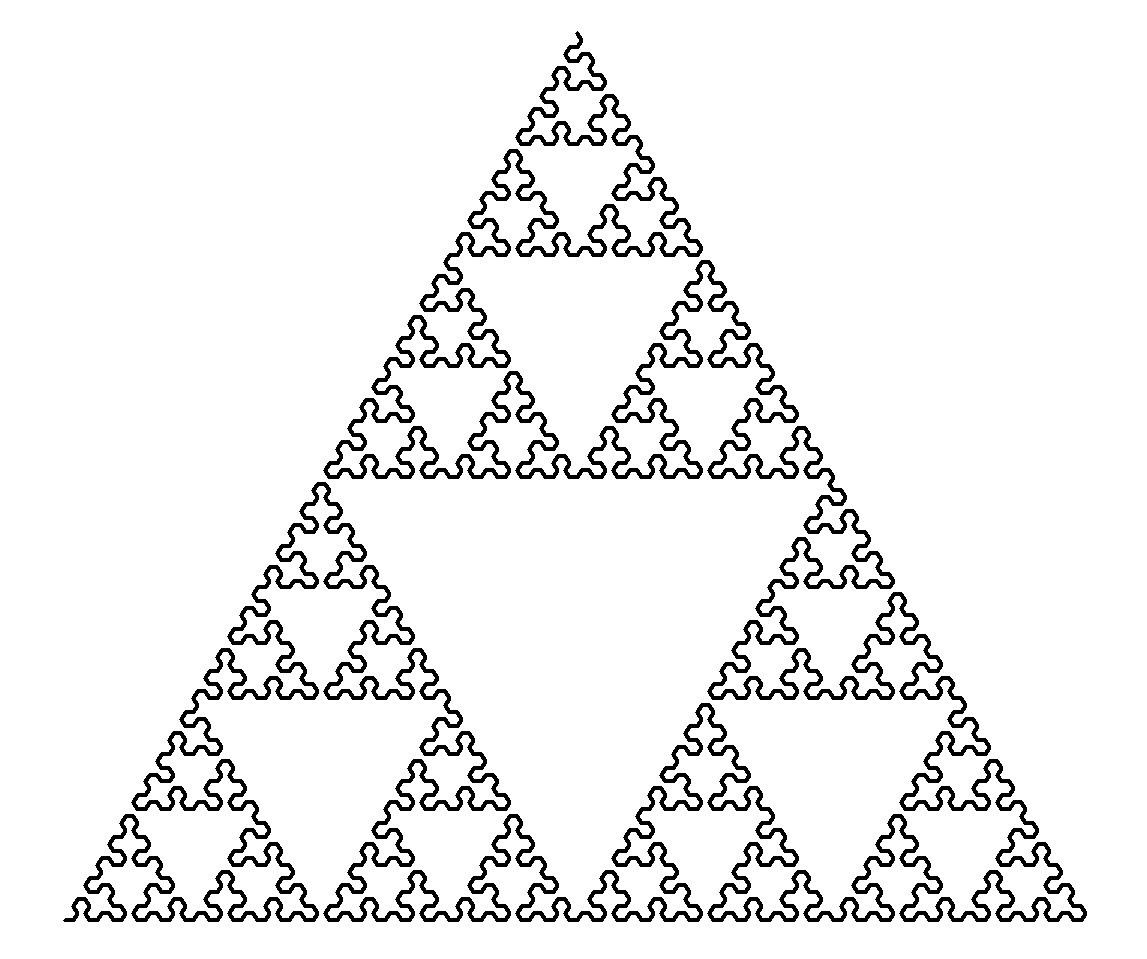
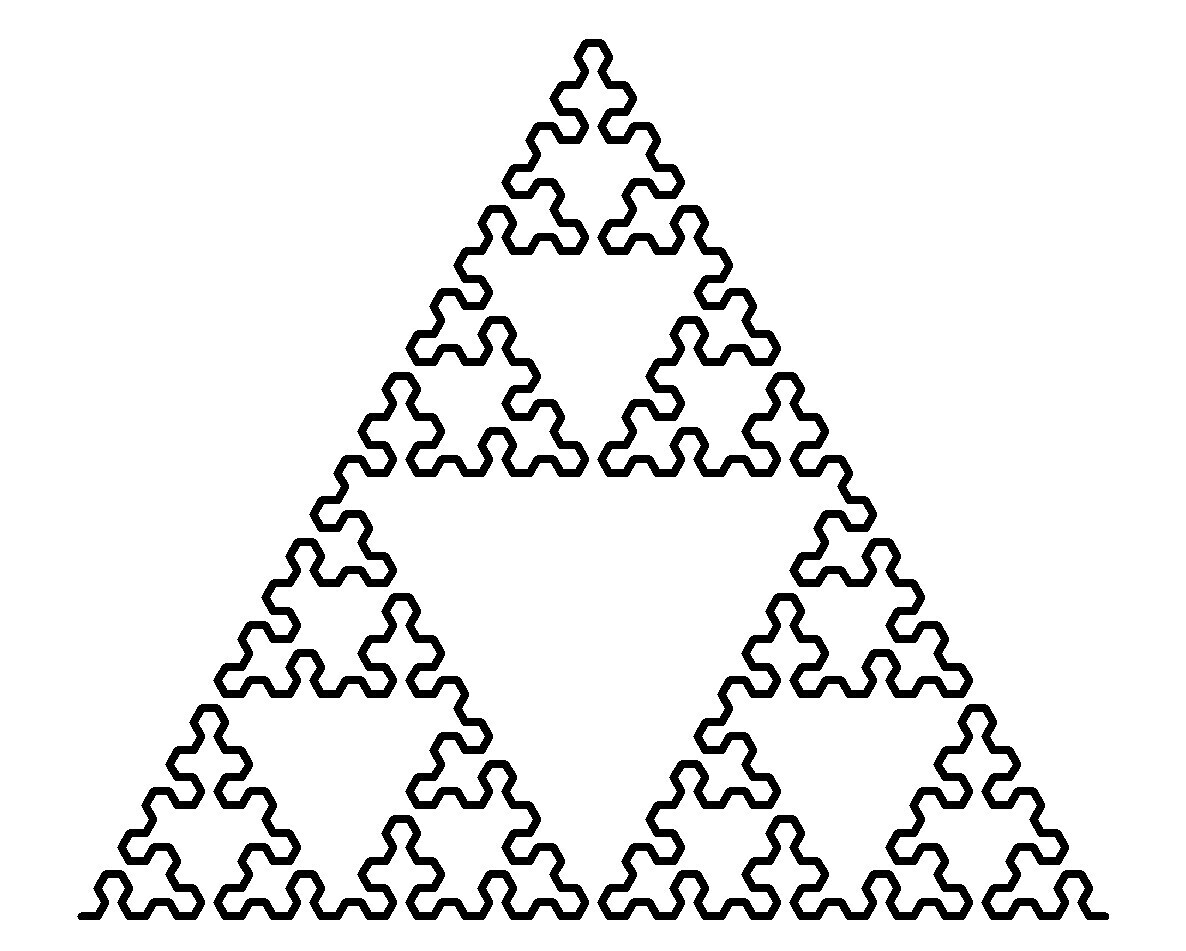
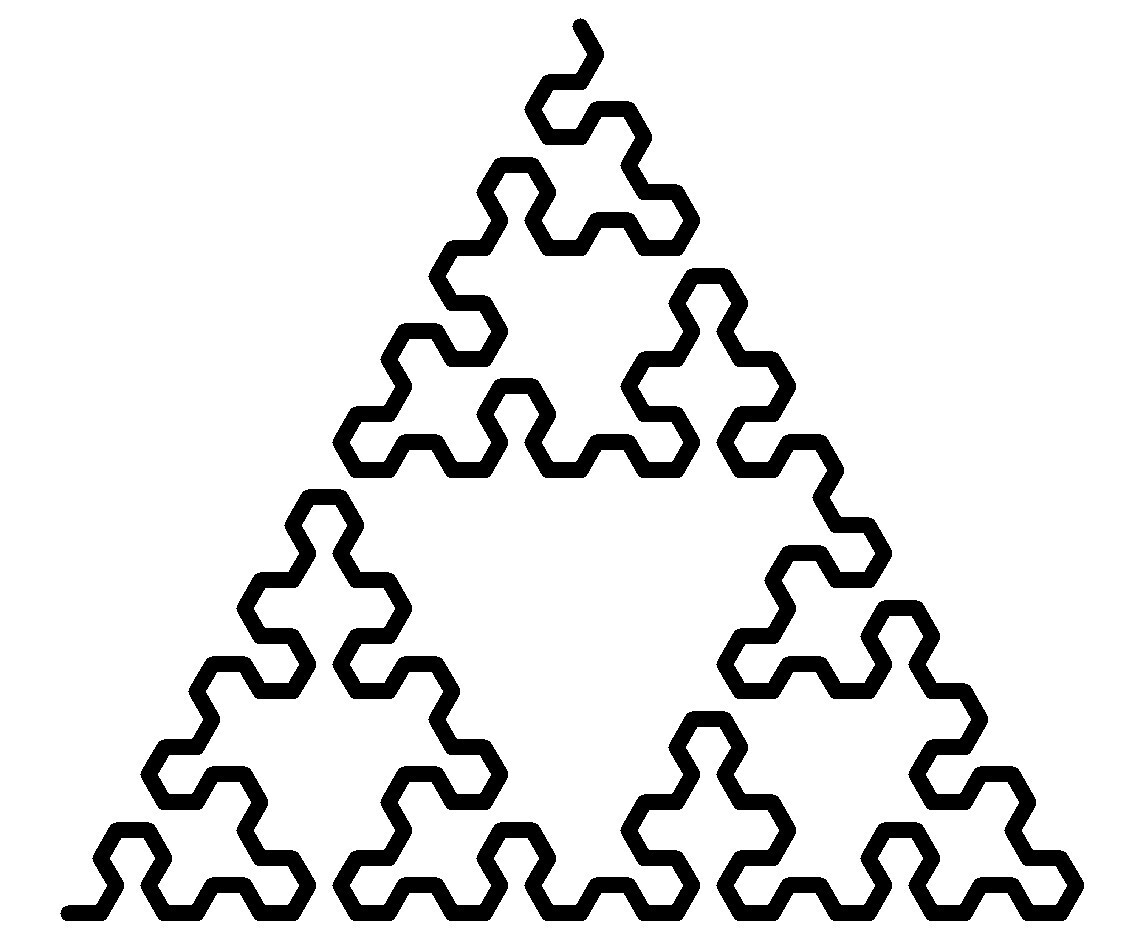
#JustForFun i created these Sierpinski triangles using #Python's #turtle module | #maths #math #programming #fractals #recursion
import logging
import turtle
import time
SPEED_INT = 5 # 1-10 where 0 is as fast as possible
logging.basicConfig(level=logging.DEBUG)
DISPLAY_WIDTH = 1620
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Sierpinski Triangle (using turtle)")
t.shape("turtle")
t.speed(SPEED_INT)
turtle.setheading(0)
# ..set start position
t.penup()
turtle.setx(-DISPLAY_WIDTH // 2)
turtle.sety(-450)
t.pendown()
start_pos = t.pos()
time.sleep(1)
def draw_recursive(i_level: int, i_direction: int):
"""Level 1 is the starting i_starting_level (0 doesn't exist)"""
logging.debug(f"{i_level * '-'} draw_recursive called with level {i_level}")
if i_level == 1:
t.forward(distance)
return
draw_recursive(i_level - 1, -i_direction)
t.left(i_direction * 60)
draw_recursive(i_level - 1, i_direction)
t.left(i_direction * 60)
draw_recursive(i_level - 1, -i_direction)
distance = 0
def draw_(i_starting_level: int, i_pen_color_channel: float = 0.0):
logging.debug(f"==== draw_ called with starting level {i_starting_level} ====")
t.penup()
t.setpos(start_pos)
t.setheading(0)
t.pendown()
global distance
distance = 1024 / (2 ** (i_starting_level - 1))
distance = min(100, distance)
pen_size = distance // 2
if pen_size < 1:
raise Exception("Pen size is smaller than one")
t.pensize(distance // 2)
t.pencolor((i_pen_color_channel,) * 3)
if i_starting_level % 2 == 0:
direction = 1
else:
direction = -1
draw_recursive(i_starting_level, direction)
# draw_(9)
pen_color_channel = 0.8
for i_starting_level in range(5, 8):
if pen_color_channel < 0:
raise Exception("Pen color channel smaller than zero")
draw_(i_starting_level, pen_color_channel)
pen_color_channel -= 0.2
t.hideturtle()
turtle.done()
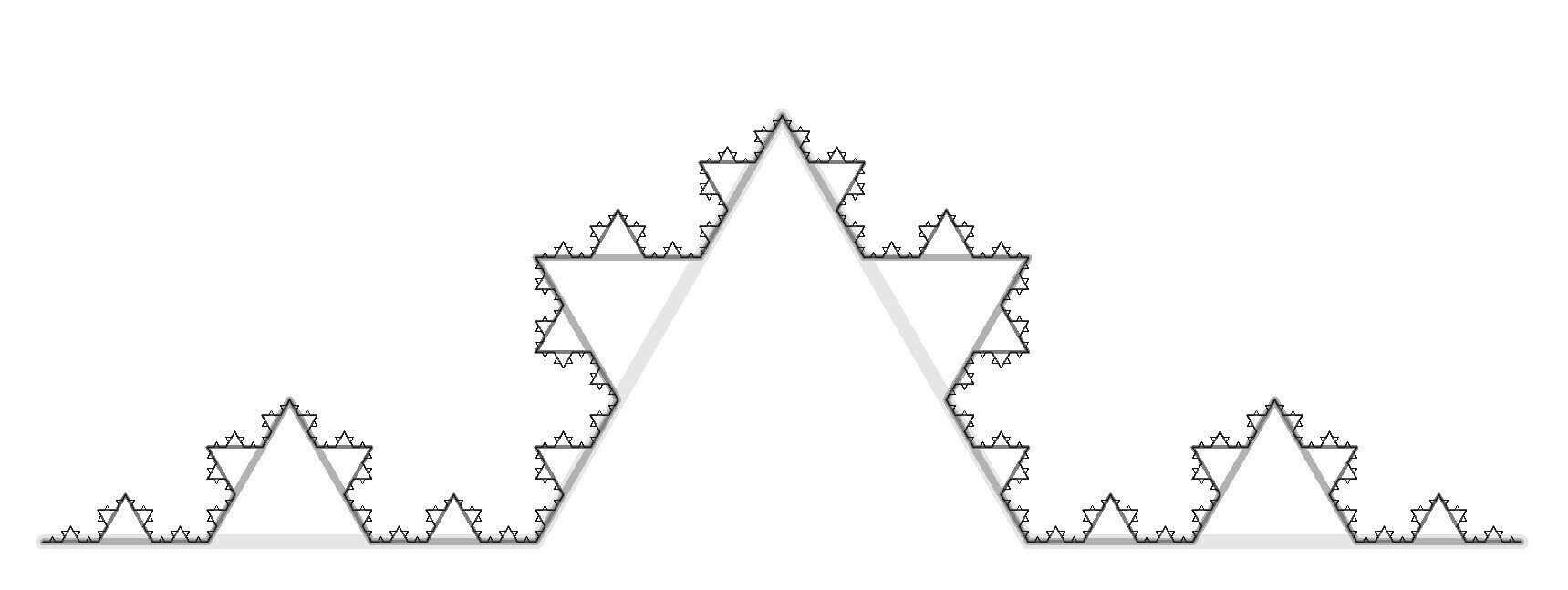
#JustForFun i created these #KochSnowflake/s using #Python's #turtle module | #maths #math #programming #fractals #recursion
import logging
import turtle
import time
SPEED_INT = 4 # 1-10 where 0 is as fast as possible
logging.basicConfig(level=logging.DEBUG)
DISPLAY_WIDTH = 1620
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Koch Snowflake")
t.shape("turtle")
t.speed(SPEED_INT)
turtle.setheading(0)
# ..set start position
t.penup()
turtle.setx(-DISPLAY_WIDTH // 2)
turtle.sety(-400)
t.pendown()
start_pos = t.pos()
time.sleep(1)
def draw_recursive(i_level: int):
"""Level 1 is the starting level (0 doesn't exist)
, i_unit_distance: int
"""
if i_level == 1:
t.forward(distance)
return
draw_recursive(i_level - 1)
t.left(60)
draw_recursive(i_level - 1)
t.right(120)
draw_recursive(i_level - 1)
t.left(60)
draw_recursive(i_level - 1)
def get_distance(i_levels_to_draw):
distance_ = DISPLAY_WIDTH / (3 ** (i_levels_to_draw - 1))
return distance_
pen_color_channel = 0.9
pen_size = 16
for i in range(2, 7):
t.penup()
t.setpos(start_pos)
t.pendown()
levels_to_draw = i
distance = get_distance(levels_to_draw)
if pen_size < 1:
raise Exception("Pen size smaller than one")
t.pensize(pen_size)
pen_size = pen_size // 2
if pen_color_channel < 0:
raise Exception("Pen color channel smaller than zero")
t.pencolor((pen_color_channel,) * 3)
pen_color_channel -= 0.2
draw_recursive(levels_to_draw)
t.hideturtle()
turtle.done()
The Mandelbulb Fractal https://www.maths.town/fractal-articles/mandelbulb/mandelbulb-all-powers/
Many people have dreamed of extending the Mandelbrot Set into three dimensions, but a problem arises because the complex numbers don’t naturally extend into 3D. The Mandelbulb fractal is an attempt to solve this dilemma. It is a 3D fractal created by extending some of the Mandelbrot’s geometric properties into the third dimension. The Mandelbulb isn't considered the true 3D Mandelbrot, but it is still a fascinating fractal.
Hey everyone, I’m #newhere. I’m interested in #fractals, #literature, #politics, #progressive, #sci-fi, #science, and #science-fiction.
just signed up on a new pod, as everyone is saying Pluspora might go down...
A Trip to #Infinity II - #Mandelbrot #Fractal #Zoom (Depth 3e2159) - YouTube
I've been fascinated by the #MandelbrotSet since I first saw an article about it in around #1985 and went to an exhibition about it at the #University of #Leeds. The particular #animation is particularly mesmerizing with the colour scheme chosen and lasts for three hours! I bet you can guess what happens at the end...
Note the #magnification factor at the end.
