#maths
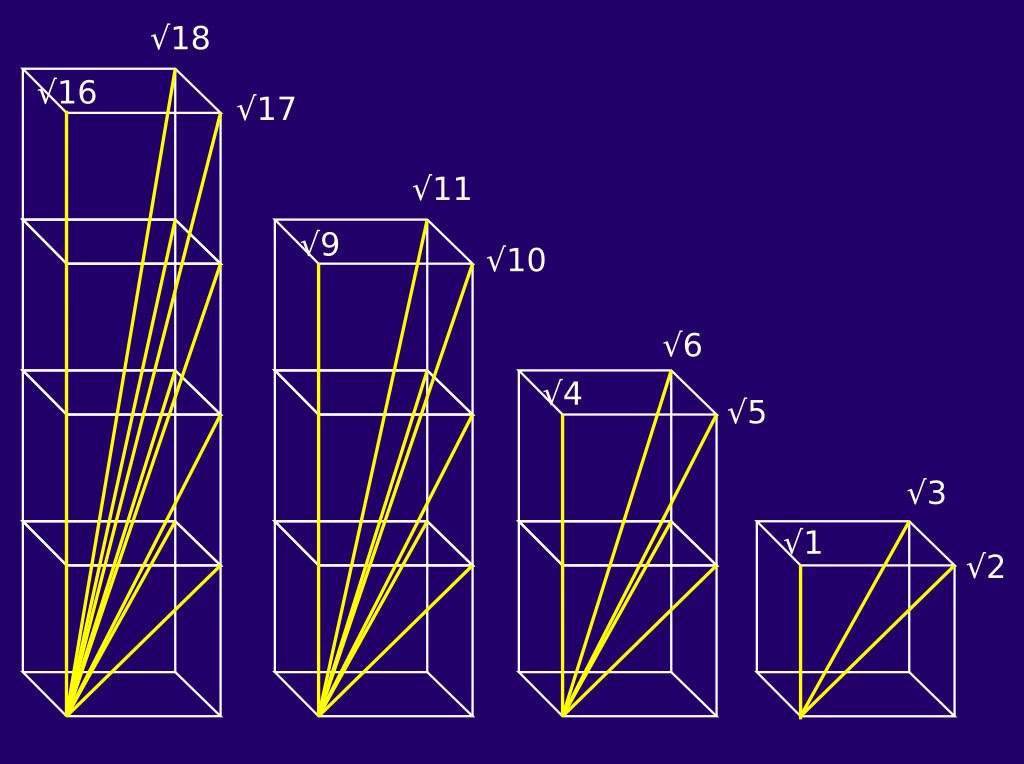
There are literally hundreds of #proofs of #Pythagorus' #Theorem and this book has about three hundred of them. It was published in the 1920s but my copy was printed to order and bound in #India. I hope it will be both a reference and a talking point.
Merci à P. (ce n'est pas le même "P." que l'autre jour 😉), élève de 1re, qui me fait confiance pour l'aider en #maths et en #physique pendant ces vacances de la Toussaint. N'hésitez pas à me contacter pour en savoir plus sur mes services et tarifs. #cours #myWork #pédagogie
Bonjour à tous,
Je traverse une période difficile et incertaine (les aléas de la vie). Je ne demande pas la charité, j'ai une activité professionnelle qui me plaît mais qui tourne actuellement au ralenti, tout coup de pouce sera le bienvenu !
Musiciens et profs de #musique : achetez mes #partitions, jouez-les, programmez-les, faites-les travailler à vos élèves : https://nicolashussein.fr/catalogue/
Prestations de copie, #arrangement etc. de partitions : https://nicolashussein.fr/prestations/
#cours de #violon #alto #solfège #écriture : https://nicolashussein.fr/cours/
À tous, musiciens ou non, vous pouvez également me soutenir :
- en regardant mes #vidéos YouTube et en les partageant autour de vous : https://www.youtube.com/@NicolasHusseinMusique
- en soutenant mon activité financièrement sur Ko-fi : https://ko-fi.com/nicolashussein
Activités annexes :
- #cours de #maths : https://www.leboncoin.fr/cours_particuliers/2400401848.htm
- tuteur de #français (conversation, correction d'écrits) : https://www.leboncoin.fr/cours_particuliers/2400400049.htm
Merci infiniment pour vos partages :-)
Bonjour à tous,
Ce n'est pas mentionné sur mon site car cela ne concerne pas la musique, mais je propose également des #cours particuliers de #maths #mathématiques à #Bourges ou en #visio : https://www.leboncoin.fr/cours_particuliers/2400401848.htm
N'hésitez pas à me contacter si besoin !
Bonne journée,
Nicolas
"Neil DeGrasse Tyson Talks about how the United States is being left behind in areas such as physics, math, and engineering comparing it to Europe and Japan which are generating more scientific papers and have better infrastructure.
Drawing upon his deep understanding of scientific trends and global dynamics, Tyson highlights the contrasting landscapes of scientific progress between the United States, Europe, and Japan. He articulates how these regions have surged ahead, not only by generating more scientific papers but also by investing in cutting-edge infrastructure and fostering collaborative research environments.
"..Throughout the video, Tyson engages in a captivating analysis of the key elements that have propelled Europe and Japan to the forefront of scientific innovation. He discusses the significance of robust funding mechanisms, visionary leadership, and educational strategies that cultivate a new generation of researchers and innovators. With an analytical yet accessible approach, Tyson addresses the underlying challenges that the United States must confront to regain its competitive edge in the global scientific arena."
https://www.youtube.com/watch?v=HgmeoDQWGLQ
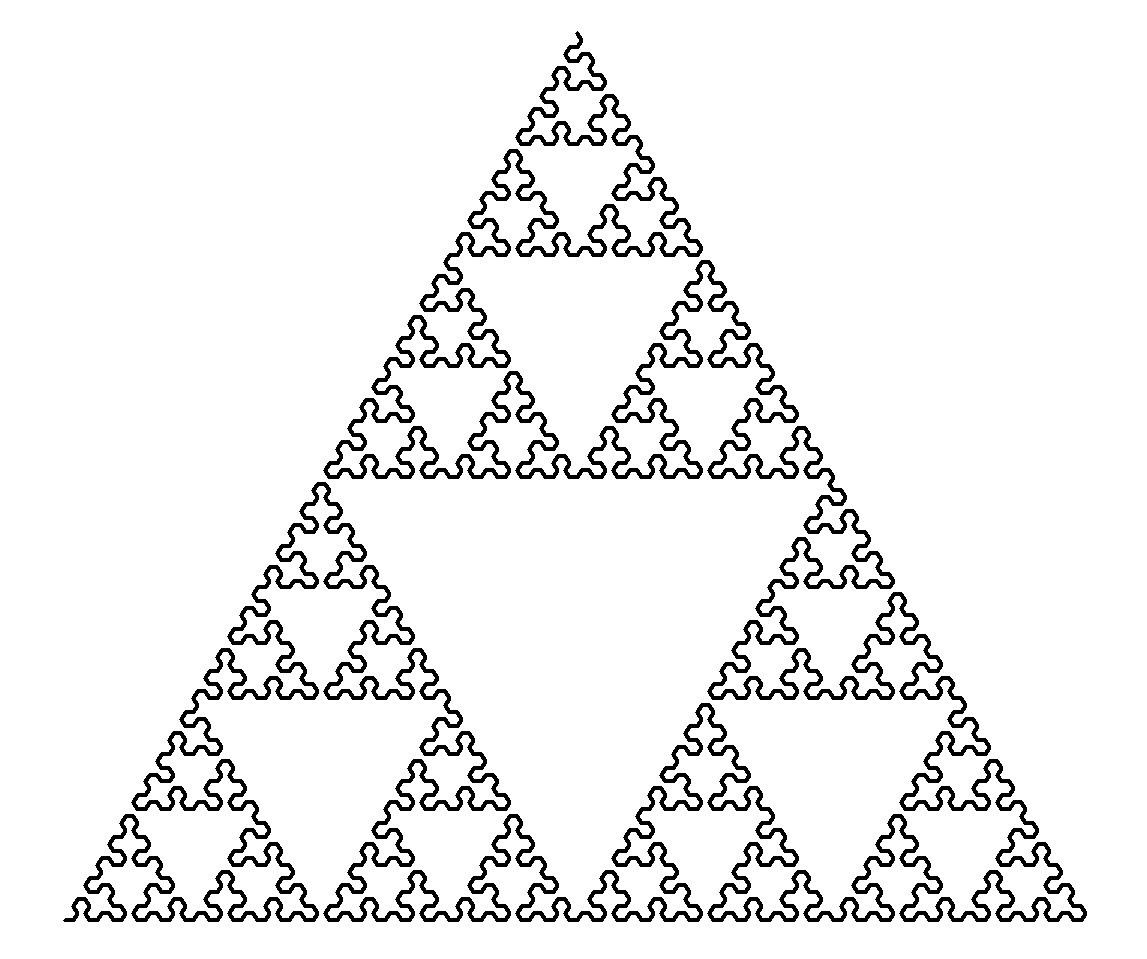
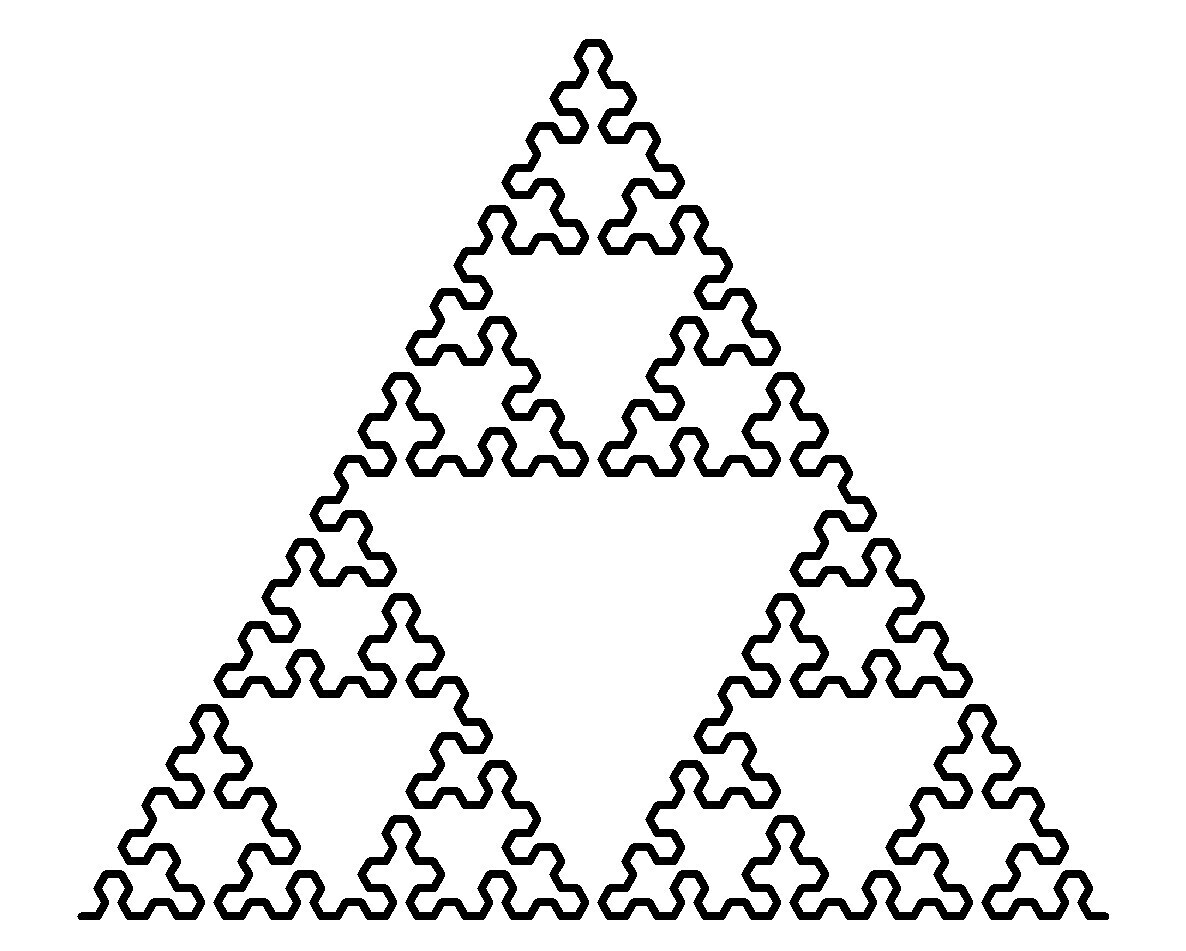
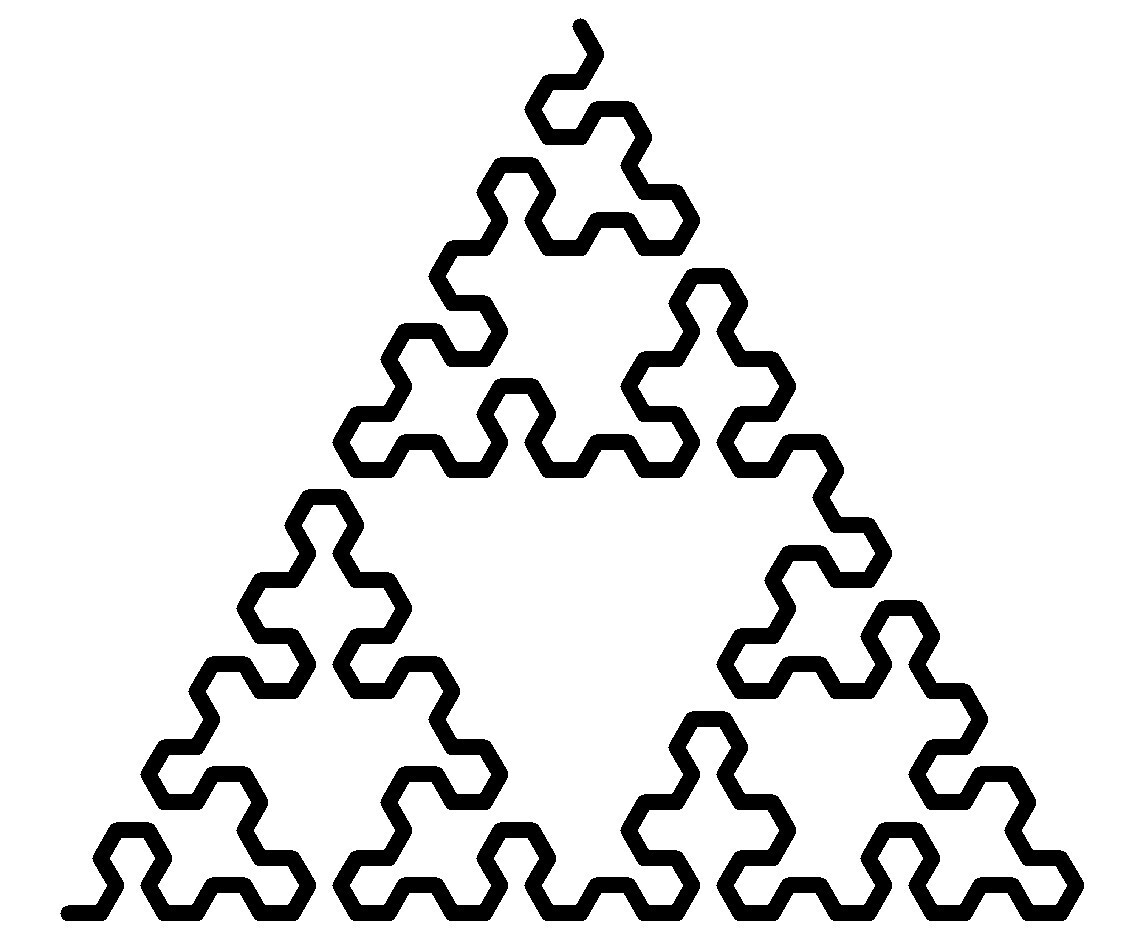
#JustForFun i created these Sierpinski triangles using #Python's #turtle module | #maths #math #programming #fractals #recursion
import logging
import turtle
import time
SPEED_INT = 5 # 1-10 where 0 is as fast as possible
logging.basicConfig(level=logging.DEBUG)
DISPLAY_WIDTH = 1620
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Sierpinski Triangle (using turtle)")
t.shape("turtle")
t.speed(SPEED_INT)
turtle.setheading(0)
# ..set start position
t.penup()
turtle.setx(-DISPLAY_WIDTH // 2)
turtle.sety(-450)
t.pendown()
start_pos = t.pos()
time.sleep(1)
def draw_recursive(i_level: int, i_direction: int):
"""Level 1 is the starting i_starting_level (0 doesn't exist)"""
logging.debug(f"{i_level * '-'} draw_recursive called with level {i_level}")
if i_level == 1:
t.forward(distance)
return
draw_recursive(i_level - 1, -i_direction)
t.left(i_direction * 60)
draw_recursive(i_level - 1, i_direction)
t.left(i_direction * 60)
draw_recursive(i_level - 1, -i_direction)
distance = 0
def draw_(i_starting_level: int, i_pen_color_channel: float = 0.0):
logging.debug(f"==== draw_ called with starting level {i_starting_level} ====")
t.penup()
t.setpos(start_pos)
t.setheading(0)
t.pendown()
global distance
distance = 1024 / (2 ** (i_starting_level - 1))
distance = min(100, distance)
pen_size = distance // 2
if pen_size < 1:
raise Exception("Pen size is smaller than one")
t.pensize(distance // 2)
t.pencolor((i_pen_color_channel,) * 3)
if i_starting_level % 2 == 0:
direction = 1
else:
direction = -1
draw_recursive(i_starting_level, direction)
# draw_(9)
pen_color_channel = 0.8
for i_starting_level in range(5, 8):
if pen_color_channel < 0:
raise Exception("Pen color channel smaller than zero")
draw_(i_starting_level, pen_color_channel)
pen_color_channel -= 0.2
t.hideturtle()
turtle.done()
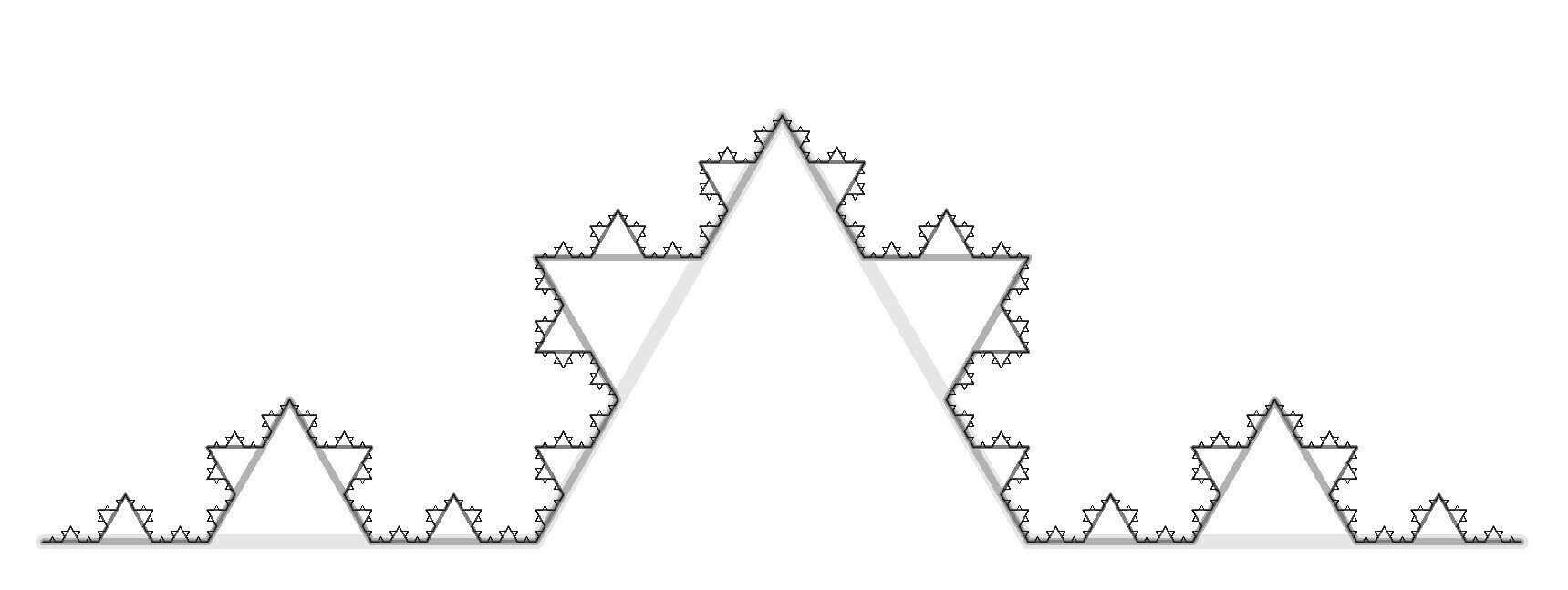
#JustForFun i created these #KochSnowflake/s using #Python's #turtle module | #maths #math #programming #fractals #recursion
import logging
import turtle
import time
SPEED_INT = 4 # 1-10 where 0 is as fast as possible
logging.basicConfig(level=logging.DEBUG)
DISPLAY_WIDTH = 1620
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Koch Snowflake")
t.shape("turtle")
t.speed(SPEED_INT)
turtle.setheading(0)
# ..set start position
t.penup()
turtle.setx(-DISPLAY_WIDTH // 2)
turtle.sety(-400)
t.pendown()
start_pos = t.pos()
time.sleep(1)
def draw_recursive(i_level: int):
"""Level 1 is the starting level (0 doesn't exist)
, i_unit_distance: int
"""
if i_level == 1:
t.forward(distance)
return
draw_recursive(i_level - 1)
t.left(60)
draw_recursive(i_level - 1)
t.right(120)
draw_recursive(i_level - 1)
t.left(60)
draw_recursive(i_level - 1)
def get_distance(i_levels_to_draw):
distance_ = DISPLAY_WIDTH / (3 ** (i_levels_to_draw - 1))
return distance_
pen_color_channel = 0.9
pen_size = 16
for i in range(2, 7):
t.penup()
t.setpos(start_pos)
t.pendown()
levels_to_draw = i
distance = get_distance(levels_to_draw)
if pen_size < 1:
raise Exception("Pen size smaller than one")
t.pensize(pen_size)
pen_size = pen_size // 2
if pen_color_channel < 0:
raise Exception("Pen color channel smaller than zero")
t.pencolor((pen_color_channel,) * 3)
pen_color_channel -= 0.2
draw_recursive(levels_to_draw)
t.hideturtle()
turtle.done()
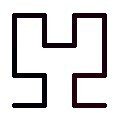
#JustForFun i created this Hilbert space-filling curve using #Python's #turtle module | #maths #math #programming
import logging
import random
import turtle
import time
SPEED_INT = 5 # 1-10 where 0 is as fast as possible
UNIT_DISTANCE = 30
logging.basicConfig(level=logging.DEBUG)
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Hilbert Space-filling Curve")
t.shape("turtle")
t.speed(SPEED_INT)
t.pensize(5)
t.pencolor((0, 0, 0))
t.penup()
turtle.setx(-500)
turtle.sety(-450)
t.pendown()
start_pos = t.pos()
time.sleep(1)
CW = 1
CCW = -1
def get_angle():
fuzzyness = random.choice(range(0, 2))
# degrees = 90 + fuzzyness
degrees = 90
return degrees
color_ = (0, 0, 0)
DIRECTION_UP = True
DIRECTION_DOWN = False
color_change_direction = (DIRECTION_UP, DIRECTION_UP, DIRECTION_UP)
def change_color():
global color_
global color_change_direction
index_to_change = random.choice(range(0, 3))
channel = color_[index_to_change]
if color_change_direction:
channel += 0.05
else:
channel -= 0.05
if channel > 1.0:
color_change_direction = not color_change_direction
channel = 1.0
elif channel < 0.0:
color_change_direction = not color_change_direction
channel = 0.0
new_color = turtle.pencolor()
new_color_list = list(new_color)
new_color_list[index_to_change] = channel
color_ = tuple(new_color_list)
turtle.pencolor(color_)
def draw_recursive(i_direction: int, i_level: int):
"""Level 1 is the starting level (0 doesn't exist)"""
if i_level == 1:
change_color()
def right_forward():
t.right(i_direction * get_angle())
t.forward(UNIT_DISTANCE)
def forward_right():
t.forward(UNIT_DISTANCE)
t.right(i_direction * get_angle())
if i_level > 1: draw_recursive(-i_direction, i_level - 1)
if i_level % 2 == 0:
right_forward()
else:
forward_right()
if i_level > 1: draw_recursive(i_direction, i_level - 1)
if i_level % 2 == 0:
t.right(-i_direction * get_angle())
t.forward(UNIT_DISTANCE)
t.right(-i_direction * get_angle())
else:
t.forward(UNIT_DISTANCE)
if i_level > 1: draw_recursive(i_direction, i_level - 1)
if i_level % 2 == 0:
forward_right()
else:
right_forward()
if i_level > 1: draw_recursive(-i_direction, i_level - 1)
turtle.setheading(90)
draw_recursive(CW, 5)
t.hideturtle()
turtle.done()
A few weeks ago, I posted an example of a #projectile #trajectory in a uniform #GravitationalField without #AirResistance. It's a school-level exercise but it was nice to produce an #animation for it. To model air resistance is a bit more tricky as any #fluid, including #air, is complex and does not necessarily behave as you might expect. A simple model for it might be to assume it is a #linear #viscous fluid offering resistance proportional to the velocity of the projectile, i.e. R = -k.v, where v is the velocity vector and k is a constant which dictates how viscous the fluid is.
Happily, this model has exact solutions so I didn't need to do any numerical integration to find the form of the displacement. Here are four different cases, including the "ideal" case k = 0. The others are k = 0.1, 1 and 10, with the middle one highlighted. The essential difference between the non-resistance case and the others is that horizontal velocity steadily decreases with time and decays towards zero exponentially. The vertical velocity is also reduced but still grows. The most viscous case (k = 10) shows terminal velocity behaviour very quickly and the projectile appears to be moving through treacle.
‘The miracle that disrupts order’: mathematicians invent new ‘Einstein’ shape | #Mathematics | The Guardian
https://www.theguardian.com/science/2023/apr/03/new-einstein-shape-aperiodic-monotile
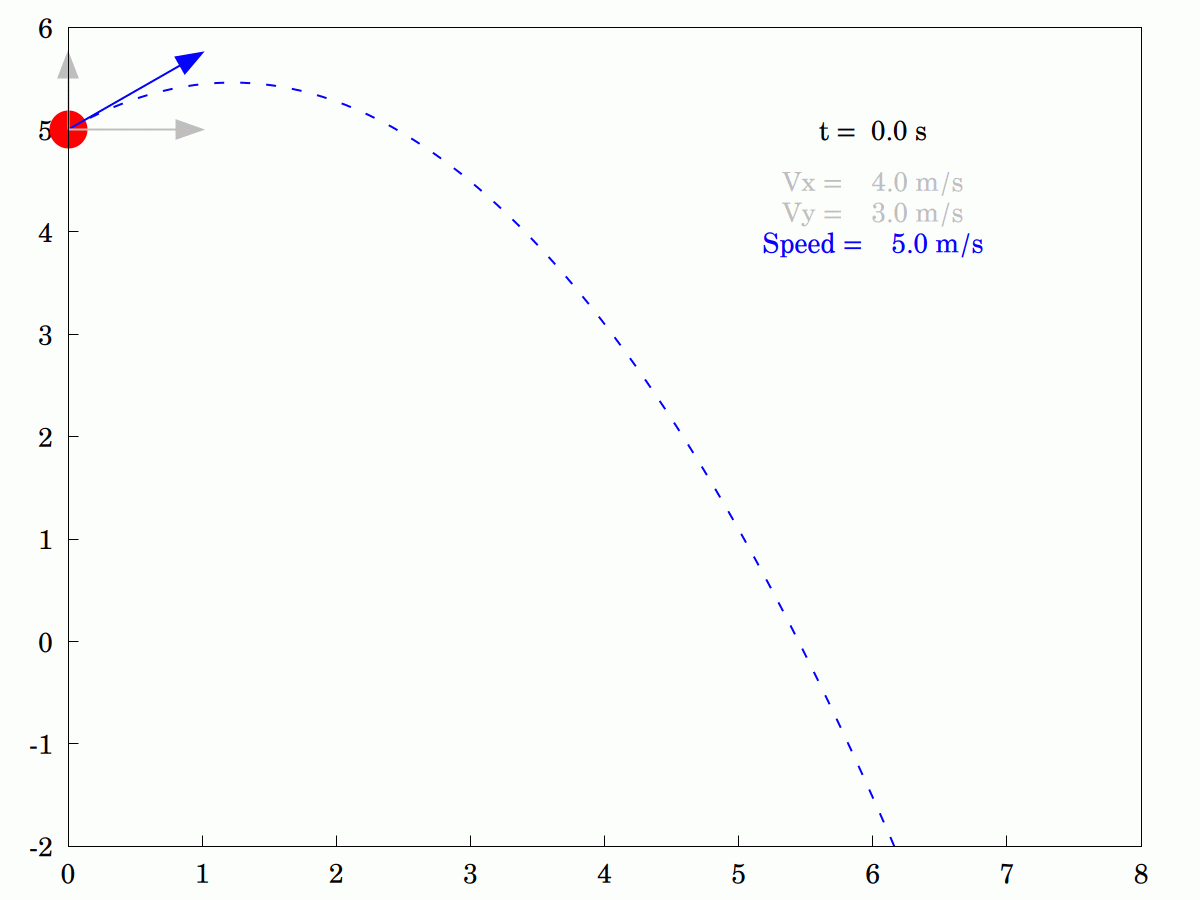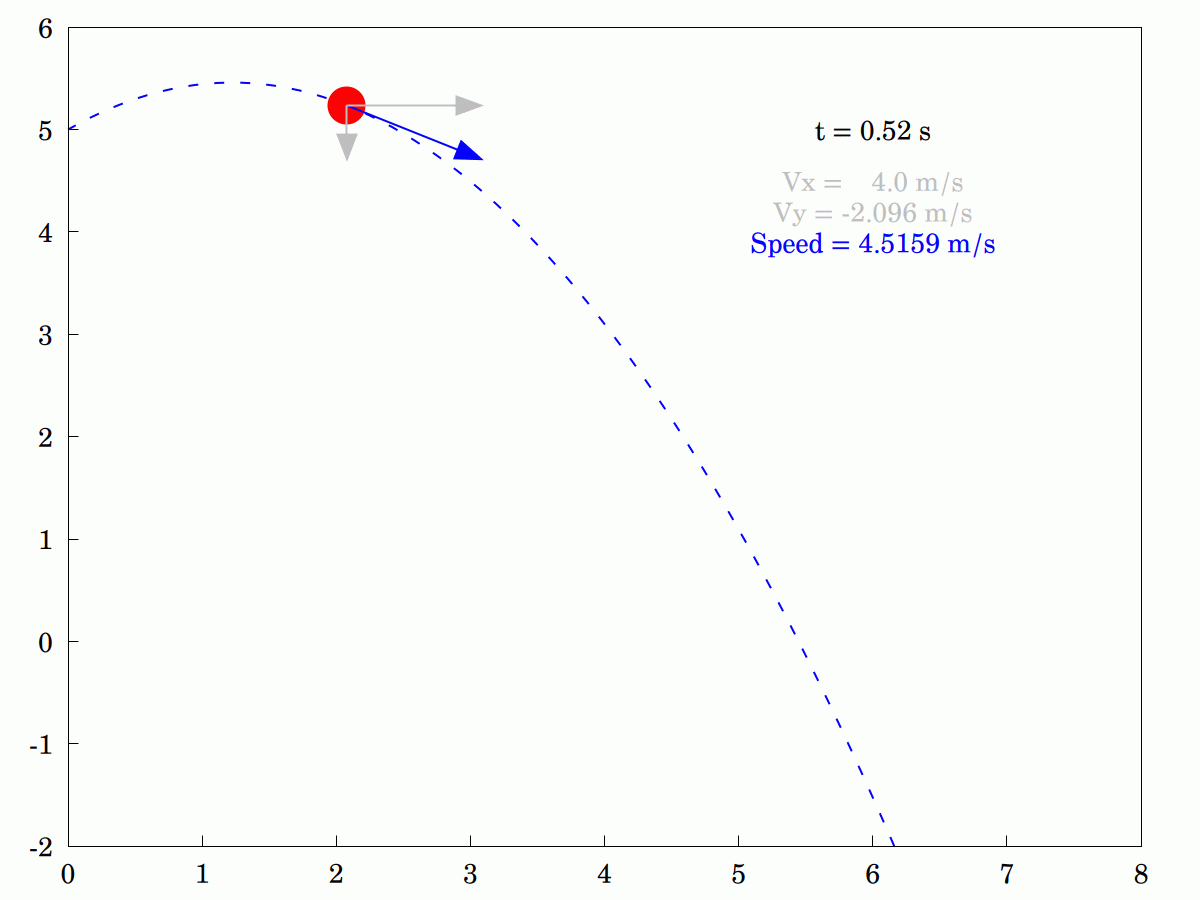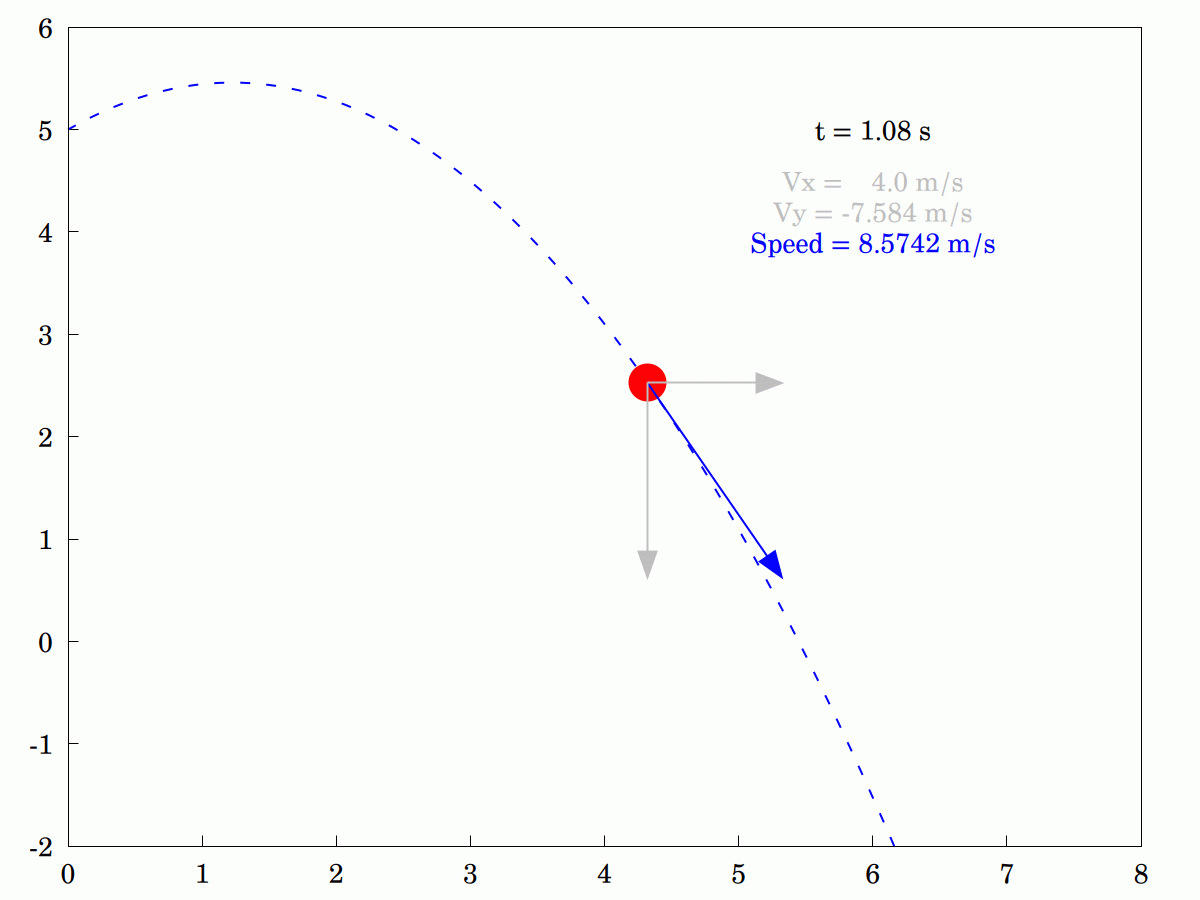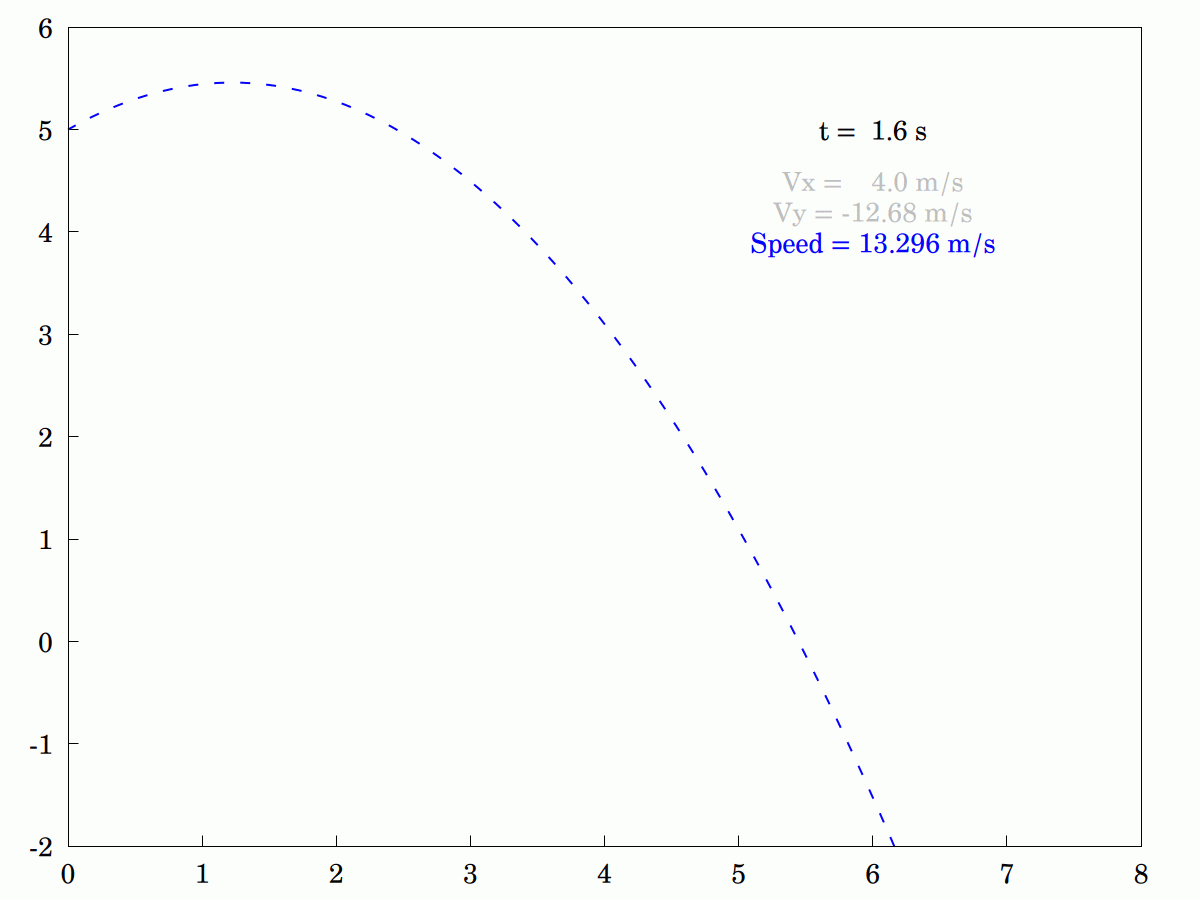
I was explaining to my wife how the #velocity #components of an idealized #projectile differ. She was having some problems understanding that only the #vertical component changes and that the #horizontal component remains constant. In the end, I knocked up this little animation to tr and explain pictorially (the program in #WxMaxima is actually interactive. so you can stop it, step through it or run it backwards if that helps).
#Maths #Mathematics #Mechanics #ConstantAcceleration #Vectors #Dynamics #MyWork #CCBYSA #FreeSoftware