A couple of nights ago, I mentioned that I spotted #Venus looking out #westwards. Well here's final incontrovertible proof that the #planet exists!
The first image is taken with an #exposure #time of 1 s and hence things look very bright even thought it was taken at #twilight.
A couple of minutes later, it was both getting darker and I used an exposure time of 1/4 s.
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #BackyardAstronnomy #Dusk
Neighbours minding their own business. I posted a #photograph of one of these #spiders yesterday (the one on the right). From a different angle, you can see another one quite close by. Each didn't seem too bothered by the presence of the other.4
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #Nature #Garden #Horticulture #Wildlife #Arachnids
This #spider has made its #web on the #vine and is here seen in the process wrapping up its prey. Note the shadow it is casting on the #leaf adjacent to it. Although not very big, I'm pretty sure it would make a good meal for a bird itself. I really like the patterns it has on its torso and legs.
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #Nature #Garden #Horticulture #Wildlife #Arachnids
#HighPressure has been dominating the #weather over the past few days with settled, #sunny and hot conditions. But now #air from other regions is moving in as is evidence by these #clouds this afternoon. The undulations are caused by oscillations in the layers of air as warmer and cooler air mix.
Looking #East.
Looking #West
I am designating this as #WhopperWeekend and in light of that, here's the biggest tomato we have harvested this year.
#MyWork #MyPhoto #CCBYSA #Horticulture #Nature #Plants #Fruit
The total harvest of #RunnerBeans this year is going to be something like 30 kg.
Here is part of today's batch.
Among them, was a whopper which was over 35 cm in length.
Talking of whoppers, a huge #BumbleBee happened to fly past while I had my camera in my hand. Luckily, I managed to #photograph it but you don't get a sense of how big this beautiful specimen was. It was about the size of a golf ball!
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #Horticulture #Wildlife #Insect #Bees
The #Moon will soon be in its #ThirdQuarter #phase but right now it's still a #WaningGibbous.
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #BackyardAstronomy #AmateurAstronomy #Gibbous
Three #WaningGibbous #phases of the #Moon in a row.
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #BackyardAstronomy #AmateurAstronomy #Gibbous
Tonight's #WaningGibbous #phase of the #Moon.
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #BackyardAstronomy #AmateurAstronomy #Gibbous
Literally a couple of years ago I posted some #AnimatedGifs of the simplest #NumericalIntegration techniques, namely the #RectangleMethod, the #TrapeziumRule and #SimpsonsRule. In the comments, @Miloslav Číž suggested that I show the errors of each method as the number of strips increases (or equivalently,the width of each decreases). I said I'd try to do it when I got time. In principle it is a simple but worthwhile request but getting a bit of time and motivation to do it is another matter. Also, I needed to a way to change the labels dynamically. Anyway, here we are.
The rectangle method is the most simple-minded and crudest method of finding the area below the curve. It converges slowly.
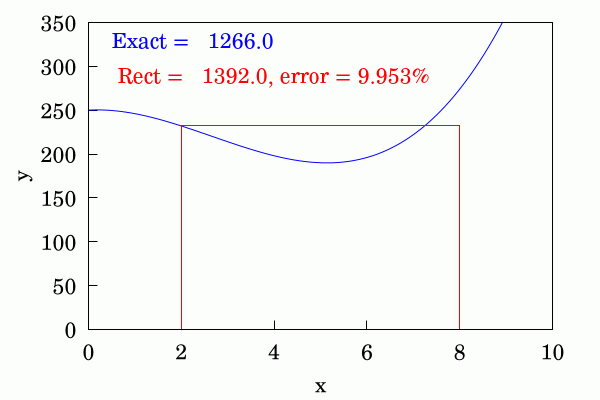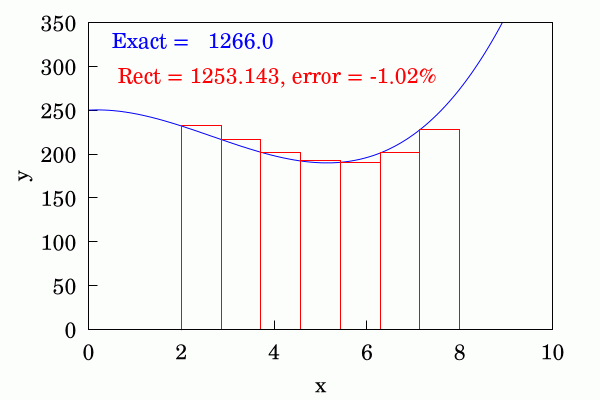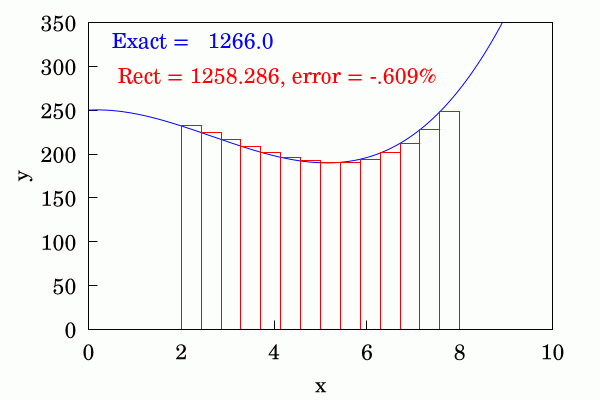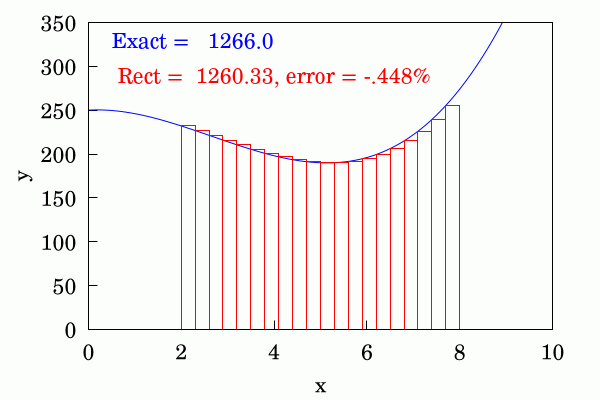
The trapezium rule is quite an improvement to the above and each area is approximated by joining up the ordinates at the beginning and end of each discrete interval with a straight line. This converges appreciably faster than the above method.
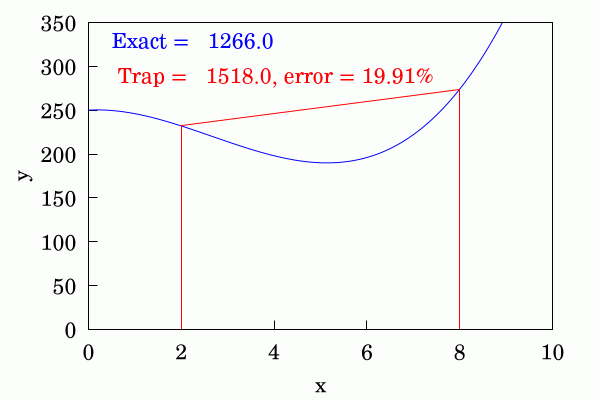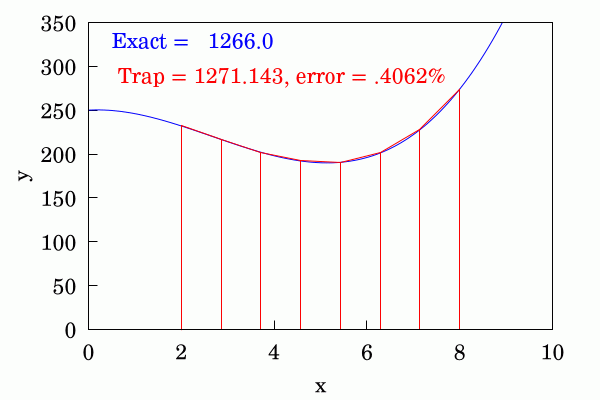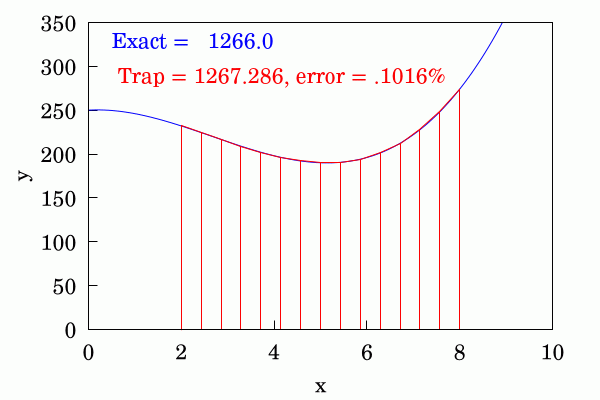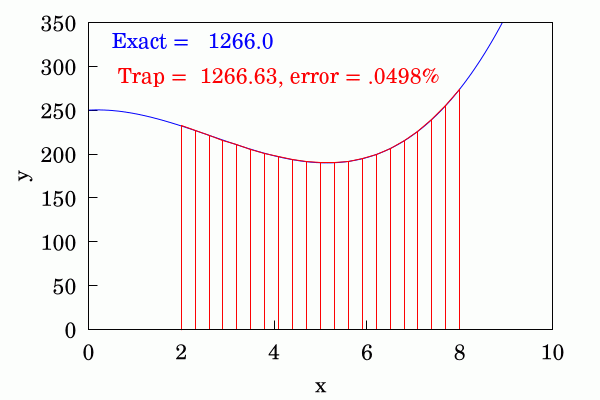
Finally the most sophisticated of the three is Simpson's rule in which pairs of adjacent strips use a #quadratic #parabola to interpolate between the ordinates. This even better at convergence than the trapezium rule. I've shown a different function here because for the function shown in the first two cases the difference between the approximation and the numerical #approximation is not discernible and the errors are very small.
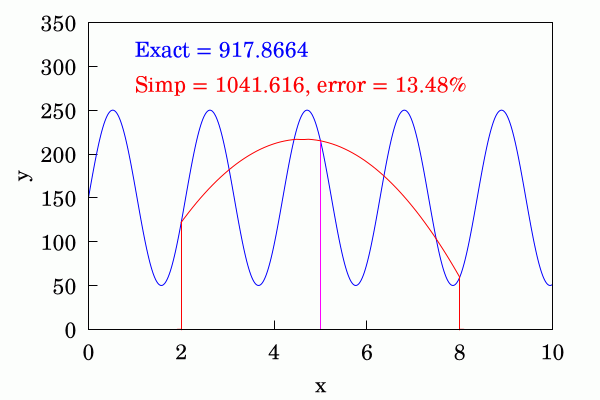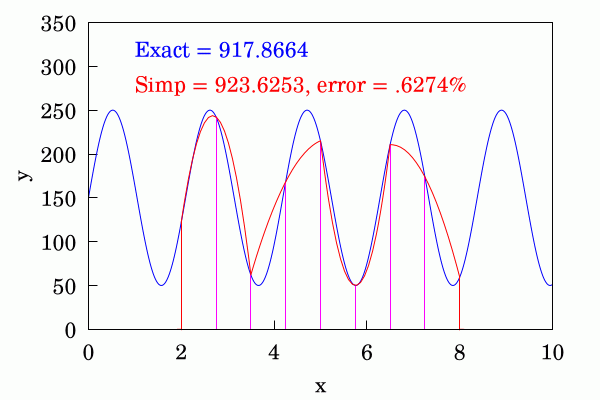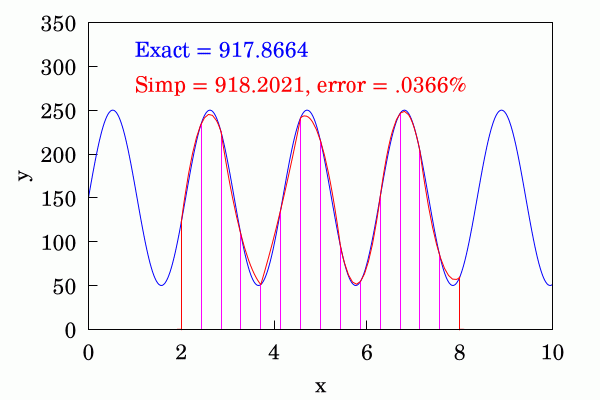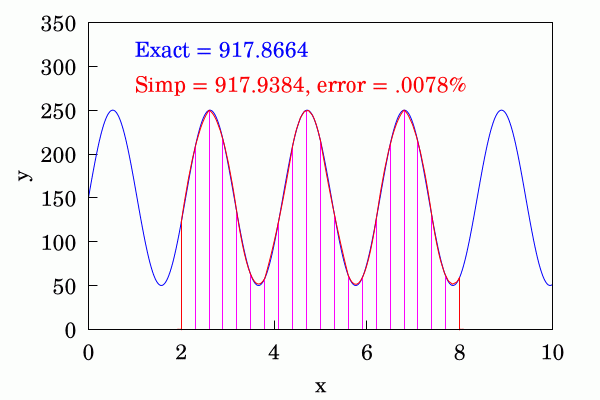
#MyWork #Mathematics #Maths #Numerics #RectangleMethod #TrapeziumRule #SimpsonsRule #FreeSoftware #CCBYSA #Wikipedia #Wikimedia
It has been a fair while since I #photographed the #Moon. There have been a few days in its cycle that I have been wanting to get and one or two for which I have #images with which I'm not really happy. Anyway, here is tonight's #WaningGibbous #phase, one day after the #FullMoon. There are a few thin #clouds but the image is quite clear.
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #BackyardAstronomy #AmateurAstronomy #Gibbous
The #tomatoes in the back #garden are finally ripening. It occurs to me that they provide a sort of reverse traffic light system with #green meaning wait, #amber meaning nearly ready and #red meaning go ahead and pick me.
#MyWork #MyPhoto #CCBYSA #DSLR #Nikon #D7000 #Nature #Plants #Fruit #Horticulture
In the #2D #elasticity, #equilibrium of #stresses can be represented on an infinitesimal rectangular element with components of both #DirectStress and #ShearStress generally acting on all four edges. If you were to rotate the rectangle, the stresses change in a precisely orchestrated fashion. In the orientation where the shear stress components vanish, we get what are called #PrincipalStresses and they and their directions can be ascertained precisely through #eigenvalue analysis. This little graphical demonstration shows one example of such a state. The #AnimatedGif was produced a routine written in #WxMaxima.
#Mathematics #TheoryOfElasticity #Mechanics #SolidMechanics #Engineering #MyWork #CCBYSA #WorkInProgress
