Greek statues dancing, brought to life by AI. The background is fuzzy and consistency between frames has a lot to be desired but the dancing movement is pretty impressive.
James Gerde uses AI to bring Hercules, Aphrodite and other Greek gods back to life - @ShadiSaleh
"'It worked when I prompted it' or the challenges of building a large language model (LLM) product".
"In no particular order, here are the major challenges we have faced when building this product."
"One of the significant challenges with using LLM APIs is the lack of SLAs or commitments on endpoint uptime and latency from the API provider."
"Prompt engineering, which involves crafting prompts for the model, is another challenge, as results using the same prompt can be unpredictable."
"Complex products with chains of prompts can further increase inconsistencies, leading to incorrect and irrelevant outputs, often called hallucinations."
"Another significant challenge is the lack of adequate evaluation metrics for the output of the Language Model."
"An incorrect result in the middle of the chain can cause the remaining chain to go wildly off track."
"Our biggest problem that led to the most delays? API endpoint deprecation."
"Trust and security issues also pose a challenge for deploying Language Models."
"The next trust issue is knowing what data was used to train these models."
"Finally, attacks on Language Models pose another challenge, as malicious actors can trick them into outputting harmful or inaccurate results."
They go on to provide a list of "Best practices for building LLM products", categorized as "finetuning and training", "prompt engineering", "vector databases", and "chains, agents, watchers".
"It worked when I prompted it" or the challenges of building an LLM product
BharatGPT is "India's own ChatGPT" -- a ChatGPT that uses the Hindi language.
The system was developed by a company in Bangalore (Bangaluru) called CoRover. Little information seems to be available about how it works. My guess is it is using a GPT model from OpenAI and fine-tuning it with additional Hindi-language text.
BharatGPT: What is India's own ChatGPT?
#solidstatelife #ai #generativemodels #lmms #gpt #india #hindi
What has AutoGPT actually accomplished? Nothing?
"Some people are reporting it has been useful as a way of generating market research, that it is good at this and faster than using the traditional GPT-4 or Bing interfaces."
"Right now, AutoGPT has a tendency to get distracted or confused or caught in a loop, to leave things half-finished, to not be that robust of an agent, and other issues like that. Positive reports seem limited to things GPT-4 or Bing can essentially do anyway, with the agent wrapper perhaps cutting down somewhat on how often you have to poke the interface with a stick to keep it pointed in a reasonable direction."
"That does not mean that all the people saying AutoGPTs are the future are wrong. AutoGPT's list of real accomplishments won't stay non-existent for long."
#solidstatelife #ai #generativemodels #nlp #lmms #gpt #rlhf #autonomous
AI models like ChatGPT use text from the internet, but the internet in the future will be more and more full of content generated by AI models like ChatGPT. Will that make the world a "closed loop -- ChatGPT all the way down"?
"Will that homogenize our writing, our thinking, and ultimately our ways of being?"
"Stylistically, large language models (LLMs) like ChatGPT might push our writing to become more sanitized. As you've probably noticed, they have a tendency to talk in a bland, conformist, Wikipedia-esque way."
"ChatGPT also privileges a 'proper' English that erases other vernaculars or languages, and the ways of seeing the world that they encode."
"Culturally, ChatGPT might reinforce a Western perspective." "If you use the models to suggest breakfast foods, they will overwhelmingly suggest Western breakfasts."
"We may become overreliant on the tech, so much so that some of our imaginative or cognitive 'muscles' gradually become weaker for lack of use."
"Asking LLMs for help at the earliest stages of our creative process will yield a certain answer that inevitably primes us to think in a certain direction."
"By the last week of that month, Bing featured three 'conversation styles,' and I had to choose between them: precise, balanced, or creative. When I chose the creative style, it answered in more off-the-wall, less predictable ways."
What happens when ChatGPT starts to feed on its own writing?
StableLM dropped yesterday. Er, day before yesterday. Or maybe the day before that. Bah, I'm going to have to get more powerful hardware. I couldn't run Stable Diffusion because my GPU wasn't powerful enough, and I probably can't run this, either.
Anyway, this is a language model made by the same people who made Stable Diffusion. More precisely, this is the first of a suite of large language models from Stability AI. This release is actually two models, one with 3 billion and one with 7 billion parameters. 15 billion and 30 billion models are promised.
They're released under a license called CC BY-SA-4.0. That means Creative Commons ShareAlike 4.0. Under that license, you can share the model and adapt the model, but have to give attribution to Stability AI, and if you modify the model, you have to put the same license on your model, requiring whoever else uses it to also give attribution to Stability AI.
Because it's an open model, I can tell you what it was trained on. It was trained on a dataset called "The Pile". "The Pile" consists of the following subsets:
Pile-CC - 227.12 GiB
PubMed Central - 90.27
Books3 - 100.96
OpenWebText2 - 62.77
ArXiv - 56.21
Github - 95.16
FreeLaw - 51.15
Stack Exchange - 32.2
USPTO Backgrounds - 22.9
PubMed Abstracts - 19.26
Gutenberg (PG-19) - 10.88
OpenSubtitles - 12.98
Wikipedia (en) - 6.38
DM Mathematics - 7.75
Ubuntu IRC - 5.52
BookCorpus2 - 6.3
EuroParl - 4.59
HackerNews - 3.9
YoutubeSubtitles - 3.73
PhilPapers - 2.38
NIH ExPorter - 1.89
Enron Emails - 0.88
Pile-CC, CC for "Common Crawl", is a collection of website crawls from 2008 onwards. PubMed Central is a dataset from the the National Center for Biotechnology Information (NCBI) and has biomedical research. Books3 is a dataset of books, with a mix of fiction and nonfiction. OpenWebText2 is a web scrape that uses upvotes on Reddit submissions as a proxy for outgoing link quality, has content up to 2020, and content in multiple languages. ArXiv you probably know because I bring you all so much stuff from there. It's a preprint server for research papers in math, computer science, and physics. GitHub is the open-source code repository website, which you all probably also know because I talk about it all the time, assuming you don't use it yourself. The Free Law Project has millions of legal opinions from federal and state courts and academic studies that analyze legal decisions. Stack Exchange is a network of websites centered around user-contributed questions and answers (including Stack Overflow, the famous question-and-answer site for coding, which was the first). USPTO Backgrounds is a dataset of background sections from patents granted by the United States Patent and Trademark Office. Wikipedia is the online encyclopedia you all know, chosen unsurprisingly because of its well-written expository prose and how it spans many domains. PubMed Abstracts has abstracts of 30 million PubMed research papers which are not part of PubMed Central mentioned above. Project Gutenberg is a dataset of classic Western literature, and the PG-19 dataset specifically consists of Project Gutenberg books from before 1919. OpenSubtitles is a dataset of English language subtitles from movies and television shows. DM Mathematics refers to the DeepMind Mathematics dataset, which consists of a collection of mathematical problems from topics such as algebra, arithmetic, calculus, number theory, and probability, formatted as natural language prompts. BookCorpus2 is a dataset of books written by "as of yet unpublished authors." Ubuntu IRC is a dataset of publicly available chat logs of all Ubuntu-related channels on the Freenode IRC chat server. EuroParl is proceedings of the European Parliament in 21 European languages from 1996 until 2012, and is considered valuable because it's a multilingual "parallel corpus" -- a corpus that has the same text in multiple languages. YouTube Subtitles is just what the name suggests: a dataset gathered from human generated (auto-generated is excluded) closed captions on YouTube. PhilPapers is a dataset of philosophy publications from the Center for Digital Philosophy at the University of Western Ontario. The NIH ExPorter dataset dataset has grant abstracts for awarded NIH grant applications from the Ex-PORTER service from 1985 to the present. Hacker News you all probably know because I send stuff from there your way. It's a news content aggregator run by Y Combinator, a startup accelerator in Silicon Valley, and articles there tend to focus on computer science and entrepreneurship. This news announcement (Stability LM) is probably there right now. There's one more, the Enron Emails dataset, which is a weird one, but apparently it was included because there generally aren't any publicly-available email datasets, but somehow Enron's emails became public in the company's demise, so it was included so the language model can learn how people talk in emails.
Brrrrp! "StableLM is trained on a new experimental dataset built on The Pile, but three times larger with 1.5 trillion tokens of content. We will release details on the dataset in due course."
So what is described above is less than what StableLM is actually trained on. If I were to guess, I'd guess all the times you see "up to" 2020 or somesuch, they caught up with data up to the current moment.
Stability AI Launches the First of its StableLM Suite of Language Models
#solidstatelife #ai #generativemodels #nlp #lmms #stabilityai #stablelm
Sparks of artificial general intelligence (AGI): Early experiments with GPT-4. So, I still haven't finished reading the "Sparks of AGI" paper, but I discovered this video of a talk by the leader of the team that did the research, Sébastien Bubeck. So you can get a summary of the research from one of the people that did it instead of me.
He talks about how they invented tests of basic knowledge of how the world works that would be exceedingly unlikely to appear anywhere in the training data, so it can't just regurgitate something it read somewhere. What they came up with is asking it how to stack a book, 9 eggs, a laptop, a bottle, and a nail onto each other in a stable manner.
They invented "theory of mind" tests, like asking where John and Mark think the cat is when they both saw John put the cat in a basket, but then John left the room and went to school and Mark took the cat out of the basket and put it in a box. GPT-4 not only says where John and Mark think the cat is, but, actually, since the way the exact question was worded, to just ask what "they" think, GPT-4 also says where the cat thinks it is.
Next he gets into definitions of intelligence that date back to the 1990s, and see how well GPT-4 does at those definitions. This is the main focus of the paper. These definitions are such things as the ability to reason, plan, solve problems, think abstractly, comprehend complex ideas, learn quickly, and learn from experience. GPT-4 succeeds at some of these but not others. For example, GPT-4 doesn't do planning. (This was before AutoGPT, for what it's worth). And GPT-4 doesn't learn from experience, as when you interact with it, it relies on its training data and its interactions with you are not part of that. (It does have a buffer that acts as short-term memory that makes the back-and-forth chat interaction coherent.)
"Can you write a proof that there are infinitely many primes, with every line that rhymes?" Just a "warm up" question.
"Draw a unicorn in TikZ." This is supposed to be hard because it should be hard to tell what code in TikZ, an annoyingly cryptic programming language, apparently (I never heard of it before) for vector graphics drawing (intended to be invoked inside LaTeX, a language for typesetting mathematical notation), creates any particular visual image without being able to "see". This was before GPT had its "multimodal" vision input added. It managed to come it with a very cartoony "unicorn", suggesting it had some ability to "see" even though it was only a language model.
"Can you write a 3D game in HTML with Javascript, I want: There are three avatars, each is a sphere. The player controls its avatar using arrow keys to move. The enemy avatar is trying to catch the player. The defender avatar is trying to block the enemy. There are also random obstacles as cubes spawned randomly at the beginning and moving randomly. The avatars cannot cross those cubes. The player moves on a 2D plane surrounded by walls that he cannot cross. The wall should cover the boundary of the entire plane. Add physics to the environment using cannon. If the enemy catches the player, the game is over. Plot the trajectories of all the three avatars."
Going from ChatGPT (GPT-3.5) to GPT-4, it goes from generating a 2D game to a 3D game as asked for.
He then gets into the coding interview questions. Here is where GPT-4's intelligence really shines. 100% of Amazon's On-Site Interview sample questions, 10 out of 10 problems solved, took 3 minutes 59 seconds out of the allotted 2 hour time slot. (Most of that time was Yi Zhang cutting and pasting back and forth.)
The paper goes far beyond the talk in this. In the paper they describe LeetCode's Interview Assessment platform, which provides simulated coding interviews for software engineer positions at major tech companies. GPT-4 solves all questions from all three rounds of interviews (titled online assessment, phone interview, and on-site interview) using only 10 minutes in total, with 4.5 hour allotted.
They challenged it to do a visualization of IMDb data. They challenge it to do a Pyplot (Matplotlib) visualization of a math formula with vague instructions about colors, and it creates an impressive visualization. They challenged it to create a GUI for a Python program that draws arrows, curves, rectangles, etc.
They challenged GPT-4 to give instructions on how to find the password in a macOS executable, which it does by telling the user to use a debugger called LLDB and a Python script. (The password was simply hardcoded into the file, so wasn't done in a way that uses modern cryptographic techniques.)
They tested GPT-4's ability to reason about (mentally "execute") pseudo-code in a nonexistent programming language (that looks something like R), which it is able to do.
"Can one reasonably say that a system that passes exams for software engineering candidates is not really intelligent?"
"In its current state, we believe that GPT-4 has a high proficiency in writing focused programs that only depend on existing public libraries, which favorably compares to the average software engineer's ability. More importantly, it empowers both engineers and non-skilled users, as it makes it easy to write, edit, and understand programs. We also acknowledge that GPT-4 is not perfect in coding yet, as it sometimes produces syntactically invalid or semantically incorrect code, especially for longer or more complex programs. [...] With this acknowledgment, we also point out that GPT-4 is able to improve its code by responding to both human feedback (e.g., by iteratively refining a plot) and compiler / terminal errors."
The reality of this capability really hit me when Google Code Jam was canceled. I've done it every year for 15 years and poof! Gone. It's because of AI. If they did Code Jam this year, they wouldn't be testing people's programming ability, they'd be testing people's ability to cut-and-paste into AI systems and prompt AI systems. And since Code Jam is a recruiting tool for Google, the implication of this is that coding challenges as a way of hiring programmers is over. And the larger implication of that is that employers don't need people who are algorithm experts who can determine what algorithm applies to a problem and competently code it any more. Or very soon. They need "programmer managers" who will manage AI systems that actually write the code.
Going back from the paper, where GPT-4 succeeded a everything, pretty much, back to the talk, in the talk he talks about GPT-4 limitations at math ability. I feel this is pretty much a moot point since GPT-4 has been integrated with Wolfram|Alpha which can perform all the arithmetic calculations desired without mistakes. But that all happened after the paper was published and this talk was recorded. Even though that was only 3 weeks ago. Things are going fast. Anyway, what he shows here is that GPT-4, as a language model, isn't terribly good at arithmetic. It does pretty well at linguistic reasoning about mathematical problems, though, to a point.
Sparks of AGI: Early experiments with GPT-4 - Sebastien Bubeck
"BlenderGPT: This addon allows you to use Blender with natural language commands using OpenAI's GPT-3.5/GPT-4"."
For those of you who do 3D modeling with Blender.
"Features: Generate Blender Python code from natural language commands, integrated with Blender's UI for easy usage, and supports Blender version 3.1 and above."
#solidstatelife #ai #generativemodels #nlp #llms #gpt #3dmodeling #blender
Wolfram|Alpha has been integrated into ChatGPT. You have to be a ChatGPT Plus user and install the Wolfram plugin from within ChatGPT. With it, you can ask questions like "How far is it from Tokyo to Chicago?" or "What is the integral of x^2*cos(2x)" and, instead of trying to answer the question linguistically, ChatGPT will realize it needs to invoke Wolfram|Alpha and pass the question to Wolfram|Alpha for a computational answer.
The article shows some of the behind-the-scenes communication between ChatGPT and Wolfram|Alpha. ChatGPT doesn't just cut-and-paste in either direction. Rather, it turns your question or into a Wolfram|Alpha query, and then re-translates-back the answer into natural language. ChatGPT can incorporate graphs from Wolfram|Alpha into its presentation as well.
"ChatGPT isn't just using us to do a 'dead-end' operation like show the content of a webpage. Rather, we're acting much more like a true 'brain implant' for ChatGPT -- where it asks us things whenever it needs to, and we give responses that it can weave back into whatever it's doing."
"While 'pure ChatGPT' is restricted to things it 'learned during its training', by calling us it can get up-to-the-moment data."
This can be based on real-time data feeds ("How much warmer is it in Timbuktu than New York now?"), or it can be based on "science-style" predictive computations ("How far is it to Jupiter right now?").
ChatGPT gets its "Wolfram Superpowers"!
#solidstatelife #ai #generativemodels #nlp #llms #openai #chatgpt #wolfram #wolframalpha
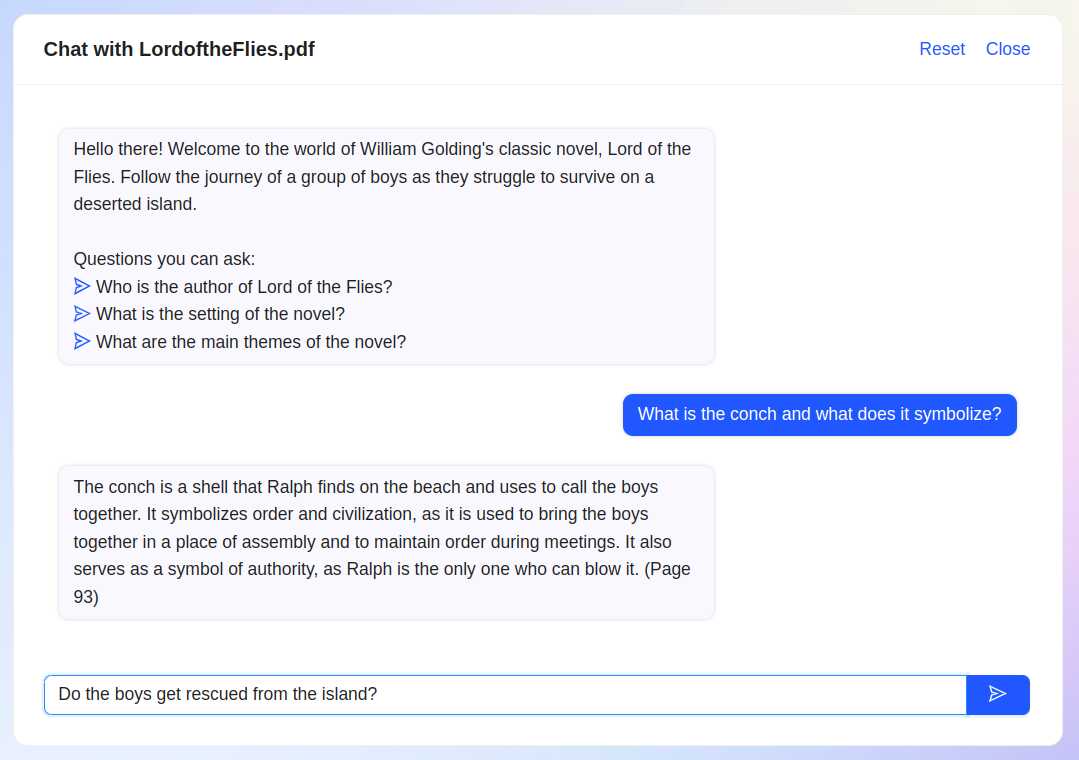
ChatPDF lets you chat with a PDF file.
To give it a whirl, I looked around on my machine and found a file called 2102.08176.pdf. I have been trying to get in the habit of immediately renaming downloaded files with something resembling their contents, but I still have lots of files lying around with cryptic names like "2102.08176.pdf". So, without opening the file and looking at the contents first, I uploaded it to ChatPDF. (You all are about to discover what kinds of files I have lying around on my machine.) Here's the conversation I had about it. All without looking at the file.
ChatPDF: Hello there! This PDF file discusses the development of flat maps that improve on the Winkel Tripel projection. The authors have developed six error measures to rate flat map projections on their verisimilitude to the sphere, and have found a new variant that performs slightly better than the Winkel Tripel.
Here are three example questions you may have about this PDF file:
What are the six error measures used to rate flat map projections?
How does the new Gott-Wagner variant compare to the Winkel Tripel in terms of error score?
What are some potential applications for these improved flat maps?
Me: What are the six error measures to rate flat map projections on their verisimilitude to the sphere?
ChatPDF: The authors of this PDF file developed six error measures to rate flat map projections on their verisimilitude to the sphere. These measures are Isotropy, Area, Flexion, Skewness, Distances, and Boundary Cuts. The first two depend on the metric of the projection, while the next two depend on its first derivatives. This information can be found on page 1 of the PDF file.
Me: What is meant by "isotropy"?
ChatPDF: In the context of this PDF file, "isotropy" refers to one of the six error measures used to rate flat map projections on their verisimilitude to the sphere. Isotropy is a measure of how well a projection preserves the relative sizes of features on the globe. Specifically, it measures how much distortion there is in the areas of regions on the map compared to their corresponding areas on the globe. The isotropy score is calculated using a root mean square (RMS) value of ln(ai/bi), where ai and bi are the semi-major and semi-minor axes of a Tissot ellipse that represents an infinitesimal circle on the globe projected onto the map. This information can be found on page 1 of the PDF file.
Me: What is a Tissot ellipse?
ChatPDF: In the context of this PDF file, a Tissot ellipse is an ellipse that represents an infinitesimal circle on the globe projected onto a map. It is used to measure how much distortion there is in the areas of regions on the map compared to their corresponding areas on the globe. The Tissot ellipse has semi-major and semi-minor axes, a and b, which are used to calculate the isotropy score, one of six error measures used to rate flat map projections on their verisimilitude to the sphere. This information can be found on page 1 of the PDF file.
Me: What is meant by "Flexion"?
ChatPDF: In the context of this PDF file, "Flexion" is one of the six error measures used to rate flat map projections on their verisimilitude to the sphere. Flexion is a measure of how much a projection bends or curves a geodesic (the shortest path between two points on a sphere) when it is projected onto a flat map. Specifically, it measures the amount of bending per degree of travel on the geodesic. A flexion score of F=1 means that there is a bending of 1 degree per degree of travel on the geodesic. This information can be found on page 2 of the PDF file.
Me: What is meant by "Boundary Cuts"?
ChatPDF: In the context of this PDF file, "Boundary Cuts" is one of the six error measures used to rate flat map projections on their verisimilitude to the sphere. Boundary cuts refer to the lines that separate regions on a map that correspond to different regions on the globe. The boundary cut error, B, is a measure of how much distortion there is in these lines compared to their corresponding lines on the globe. Specifically, it measures the length of the boundary cut in degrees divided by 720°. A boundary cut of 180° has an error of B=0.25, while a boundary cut of 360° has an error twice as bad as a boundary cut of 180° because it is like making two boundary cuts of 180° in a row. Error values for some standard map projections can be found in Table I on page 2 of the PDF file.
Me: What is meant by "Skewness"?
ChatPDF: In the context of this PDF file, "Skewness" is one of the six error measures used to rate flat map projections on their verisimilitude to the sphere. Skewness is a measure of how much a projection accelerates in a forward or backward direction when traveling along a geodesic (the shortest path between two points on a sphere) that is projected onto a flat map. Specifically, it measures the amount of acceleration per degree of travel on the geodesic. A skewness score of S=1 means that there is an acceleration of 1 degree per degree of travel on the geodesic. On conformal maps like the complete stereographic, flexion and skewness errors are equal, in that case being F=S=1. This information can be found on page 2 of the PDF file.
Me: What is meant by "Area"?
ChatPDF: In the context of this PDF file, "Area" is one of the six error measures used to rate flat map projections on their verisimilitude to the sphere. Area refers to how much distortion there is in the sizes of regions on a map compared to their corresponding sizes on the globe. The area error, A, is a measure of how much larger or smaller a region appears on the map compared to its corresponding region on the globe. Specifically, it measures the ratio of the area on the map to the area on the globe. An area score of A=1 means that there is no distortion in area, while an area score greater than 1 means that regions are enlarged and an area score less than 1 means that regions are shrunk. Error values for some standard map projections can be found in Table I on page 2 of the PDF file.
Me: Of the six error measures, do the authors consider them all of equal value, or are there some that they consider more important than others?
ChatPDF: The authors of the PDF file do not consider all six error measures to be of equal value. In fact, they argue that some error measures are more important than others. Specifically, they argue that the errors in area, distance, and angle are more important than the errors in flexion, skewness, and boundary cuts. This is because errors in area, distance, and angle have a more direct impact on how accurately a map represents the globe. The authors also note that boundary cuts and skewness are required in the error budget to avoid terrible maps winning the overall errors contest. This information can be found on page 2 and page 8 of the PDF file.
Me: What is the overall errors contest?
ChatPDF: The overall errors contest referred to in the PDF file is a competition between different flat map projections to determine which one has the lowest overall error. The overall error is calculated as a weighted sum of the six individual error measures (area, distance, angle, flexion, skewness, and boundary cuts), with weights chosen to reflect the relative importance of each measure. The goal of this competition is to find the best possible flat map projection that accurately represents the globe. This information can be found on page 2 of the PDF file.
Me: What is the best flat map projection found, according to this paper?
ChatPDF: According to the PDF file, the best flat map projection found is a new class of flat double-sided maps (like phonograph records) which have correct topology and vastly improved error scores. The azimuthal equidistant version of this map has an error score of 0.881, making it the most accurate flat map of Earth yet. This information can be found on page 1 and page 21 of the PDF file.
Me: Does the best flat map projection found have a name?
ChatPDF: The PDF file does not mention a specific name for the new class of flat double-sided maps that are considered the most accurate flat maps of Earth yet. However, it does describe them as being like phonograph records and having correct topology. The azimuthal equidistant version of this map has an error score of 0.881, which is significantly better than any other flat map projection tested in the paper. This information can be found on page 1 and page 21 of the PDF file.
Me: Why does the the best flat map projection found have to be double-sided (like phonograph records)?
ChatPDF: The best flat map projection found in the PDF file is double-sided (like phonograph records) because it allows for a Northern Hemisphere map to be on one side of the map and a Southern Hemisphere map to be on the other side. This is useful because it allows for the North Circumpolar stars to be shown in the center of the Northern Hemisphere map, and the map can be rotated in your hand to follow the rotation of the sky. Additionally, double-sided maps have correct topology and vastly improved error scores compared to one-sided maps. This information can be found on page 1 and page 31 of the PDF file.
Me: How does the azimuthal equidistant version of the best flat map projection work?
ChatPDF: The azimuthal equidistant version of the best flat map projection found in the PDF file is a double-sided disk that uses an Azimuthal Equidistant projection. This projection preserves distances from the center point of the map, making it useful for navigation and measuring distances. The map has a uniform scale along meridians and is a compromise projection like the Winkel Tripel. Errors in isotropy and area are less noticeable, and local shapes are π/2:1 elongated at the edge. Antarctica does not look too small, and Australia does not look too squashed. In sums of squares of normalized errors in isotropy, area, flexion, skewness, distances, and boundary cuts, this is the best overall flat map yet produced with an error score of 0.881. This information can be found on page 18 and page 20 of the PDF file.
Me: What is the Gott-Wagner variant?
ChatPDF: The Gott-Wagner variant is a map projection that is described in the PDF file as being useful and having a slightly better error score than the Winkel Tripel projection. The Gott-Wagner variant is not described in detail, but it is mentioned on page 1 of the PDF file as being presented alongside the new class of flat double-sided maps that are considered to be the most accurate flat maps of Earth yet.
Me: What applications are there for the the best flat map projection found?
The best flat map projection found in the PDF file has several potential applications. The map can be used for navigation and measuring distances because it preserves distances from the center point of the map. It can also be used for educational purposes, as it provides an accurate representation of the Earth's surface with correct topology. Additionally, the double-sided nature of the map allows for a Northern Hemisphere map to be on one side and a Southern Hemisphere map to be on the other side, which is useful for showing North Circumpolar stars in the center of the Northern Hemisphere map and following the rotation of the sky. This information can be found on page 1 and page 31 of the PDF file.
Me: What is the importance of showing North Circumpolar stars in the center of the Northern Hemisphere map?
ChatPDF: Showing North Circumpolar stars in the center of the Northern Hemisphere map is important because it allows for the map to be rotated in your hand to follow the rotation of the sky. This is useful for stargazing and navigation purposes. Additionally, North Circumpolar stars are always visible in the night sky from a given location in the Northern Hemisphere, so they are a useful reference point for finding other stars and constellations. This information can be found on page 31 of the PDF file.
All in all, pretty impressive! The one question I have at this point is: was all this accurate? To determine that, I need to actually open the file and read it myself. I'm also curious what's in the file that I didn't think to ask about.
The experience reminds me very much of my late-night conversations with ChatGPT, except this time it's about a specific paper.
#solidstatelife #llms #nlp #generativemodels #chatbots #chatgpt
Generating music from text. You can give it a text description like, "The main soundtrack of an arcade game. It is fast-paced and upbeat, with a catchy electric guitar riff. The music is repetitive and easy to remember, but with unexpected sounds, like cymbal crashes or drum rolls."
Go listen to the examples now.
How does it work?
"Creating text descriptions of general audio is considerably harder than describing images. First, it is not straightforward to unambiguously capture with just a few words the salient characteristics of either acoustic scenes (e.g., the sounds heard in a train station or in a forest) or music (e.g., the melody, the rhythm, the timbre of vocals and the many instruments used in accompaniment). Second, audio is structured along a temporal dimension which makes sequence-wide captions a much weaker level of annotation than an image caption."
"To address the main challenge of paired data scarcity, we rely on MuLan, a joint music-text model that is trained to project music and its corresponding text description to representations close to each other in an embedding space."
Here's that word "embedding" that makes sense to AI researchers but not to people outside. Remember, "embeddings" started out as a way of representing words in a way that is related to their meaning. They are big vectors and words with similar meaning are located in the same area of a high-dimensional space. Here, the embeddings don't represent words, they represent sounds that have meaning, such as musical notes.
"This shared embedding space eliminates the need for captions at training time altogether, and allows training on massive audio-only corpora. That is, we use the MuLan embeddings computed from the audio as conditioning during training, while we use MuLan embeddings computed from the text input during inference."
"By making no assumptions about the content of the audio signal, AudioLM learns to generate realistic audio from audio-only corpora, be it speech or piano music, without any annotation."
"Casting audio synthesis as a language modeling task in a discrete representation space, and leveraging a hierarchy of coarse-to-fine audio discrete units (or tokens), AudioLM achieves both high fidelity and long-term coherence over dozens of seconds."
MusicLM is an extension of AudioLM specifically for music. It is trained on a large unlabeled dataset of music. The tokenization of the embeddings is improved by incorporating an audio compression system called SoundStream. It creates 2 separate types of tokens, one for high-level concepts for modeling long-tem structure, and another for low-level acoustics. The language model MusicLM is built on is called w2v-BERT, which has 600 million parameters. They did a weird thing where they rip the model open, extract embeddings from the 7th layer, and cluster them, to produce 25 semantic tokens per second of audio. The network learns a mapping from MuLan tokens to semantic tokens this way.
What comes out of this process is a serious of audio tokens that get fed into the SoundStream decoder, instead of the encoder which is what is used during the training. The resulting audio has a bitrate of 24 khz, so not top quality but sounds ok.
MusicLM: Generating Music From Text
#solidstatelife #ai #generativemodels #music #audiogeneration
Zork + Imogen. What does the world of Zork, the 1981 video game, look like? A Google team uses Imogen to create a visual version of the game. They don't simply pipe the text into Imogen; instead, they modify the game to reveal internal game state that the game knows but isn't included in every text output, which helps maintain continuity during the interaction with the player.
AdventurImagen - Zork meets Google's Imagen generative imagery - Matt Walsh
#solidstatelife #ai #generativemodels #computervision #imogen
"Since releasing their debut single I'm Real in 2021, K-pop girl group Eternity have racked up millions of views online. They sing, dance and interact with their fans just like any other band. In fact, there's mainly one big difference between them and any other pop group you might know -- all 11 members are virtual characters. Non-humans, hyper-real avatars made with artificial intelligence."
You wouldn't think they're AI from the video (below). They look like humans. The video is from a year ago but I just found out about this story.
"The business we are making with Eternity is a new business. I think it's a new genre,' says Park Jieun, the woman behind Eternity."
"The advantage of having virtual artists is that, while K-pop stars often struggle with physical limitations, or even mental distress because they are human beings, virtual artists can be free from these."
Yes, the K-pop industry is legendary for putting its performers through the wringer.
"Greg Rutkowski is an artist with a distinctive style, known for creating fantasy scenes of dragons and epic battles. Rutkowski has now become one of the most popular names in AI art, despite never having used the technology himself."
"The generators are being commercialized right now, so you don't know exactly what the final output will be of your name being used over the years." -- Greg Rutkowski
#solidstatelife #ai #generativemodels #stablediffusion #openai #aiart
"A woman with flowers in her hair in a courtyard, in the style of ..." and then you can pick from 1,590 artists. Aditya Shankar was wondering how Stable Diffusion would draw what would otherwise be the exact same prompt except you can see how 1,500+ artists would have drawn it.
I put a prompt in stable diffusion to see how 1500+ artists would have drawn it
#solidstatelife #ai #generativemodels #diffusionmodels #stablediffusion
AI model to populate virtual worlds with 3D objects, such as vehicles, furniture, animals, and so on, and characters. Basically what it does is take 2D art and turn it into 3D objects. In fact the model is called GET3D. Outputs triangles and meshes and high-fidelity textures. You can also use text to further modify the objects. Can generate unlimited random variations of an object.
NVIDIA GET3D: AI model to populate virtual worlds with 3D objects and characters - NVIDIA Developer
#solidstatelife #ai #computervision #generativemodels #videogames #nvidia
"'Salt' resembles many science-fiction films from the '70s and early '80s, complete with 35mm footage of space freighters and moody alien landscapes. But while it looks like a throwback, the way it was created points to what could be a new frontier for making movies."
"Fabian Stelzer creates images with image-generation tools such as Stable Diffusion, Midjourney and DALL-E 2. He makes voices mostly using AI voice generation tools such as Synthesia or Murf. And he uses GPT-3, a text-generator, to help with the script writing."
"There's an element of audience participation, too."
This guy is using AI to make a movie -- and you can help decide what happens next | CNN Business
#solidstatelife #ai #nlp #computervision #generativemodels #filmmaking
Take 4 images of a subject, give it to this new Google AI, and it can change the background behind your little doggy... and make your little doggy swimming, sleeping, in a bucket, and getting a haircut. Similarly, if you have a pair of stylish sunglasses, you can ask a bear to wear it, make a cool product photo, or put it in front of the Eiffel Tower. Put your favorite teapot into different contexts, see it in use, or see what it would look like if it was transparent. Create art renditions of your test subject from legendary artists of the past.
Google's new AI: dog goes in, statue comes out! - Two Minute Papers
#solidstatelife #ai #computervision #generativemodels #aiart
"The difference between human-drawn bad bicycles and AI-generated photorealistic 5-6 legged horses is important and insightful. Humans are largely unable to reproduce the visual likeness of something. But they know what the parts are (2 wheels + 2 pedals + handbar + saddle). On the other hand, a deep learning model is excellent at reproducing local visual likeness (what it's fitted on), yet it has no understanding of the parts & their organization.
"A 5-year old that draws disproportionate stick figures will still draw horses with 4 legs and 1 head and 2 eyes."
"This is the difference between discrete and continuous world models. Between a graph and a differentiable curve."
The difference between human-drawn bad bicycles and AI-generated photorealistic 5-6 legged horses
/cdn.vox-cdn.com/uploads/chorus_asset/file/24054867/ai_generated_pokemon.jpg)
