5 Persons are tagged with #mathematics

#mathematics

mkwadee@diasp.eu
Khurram Wadee

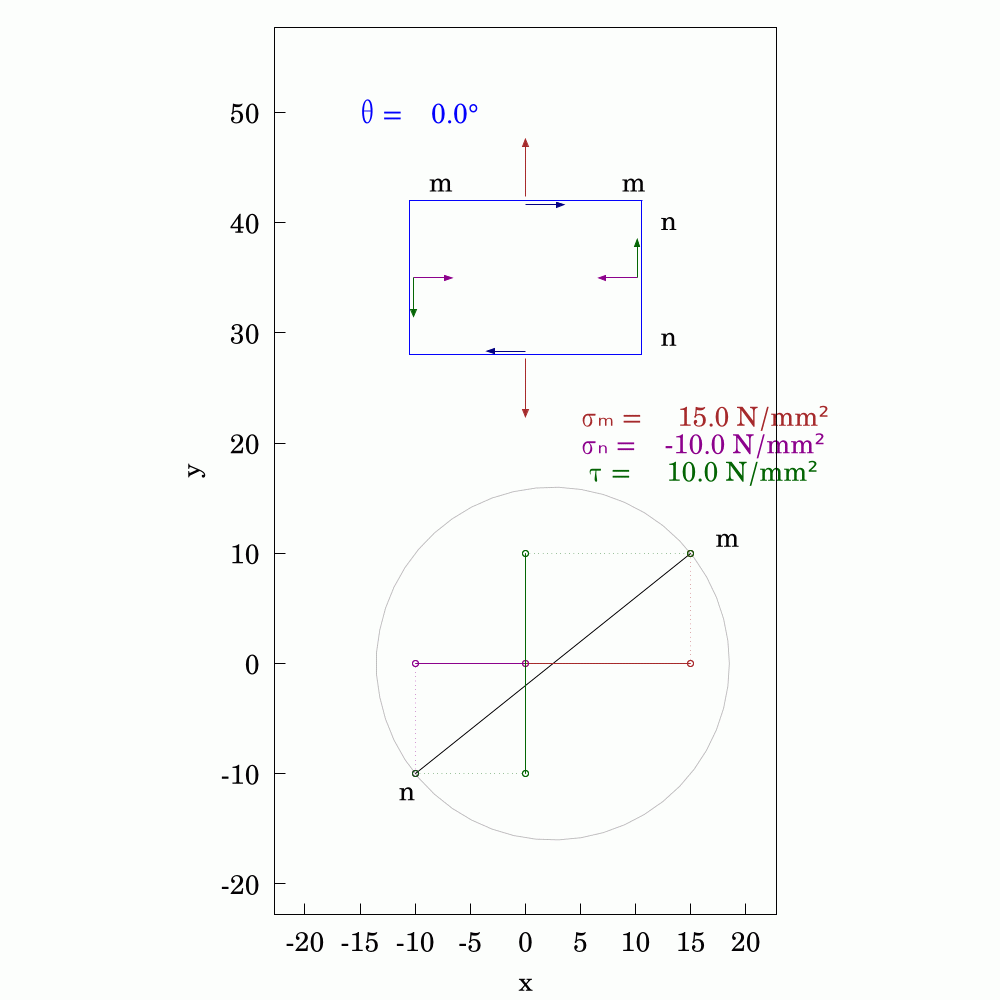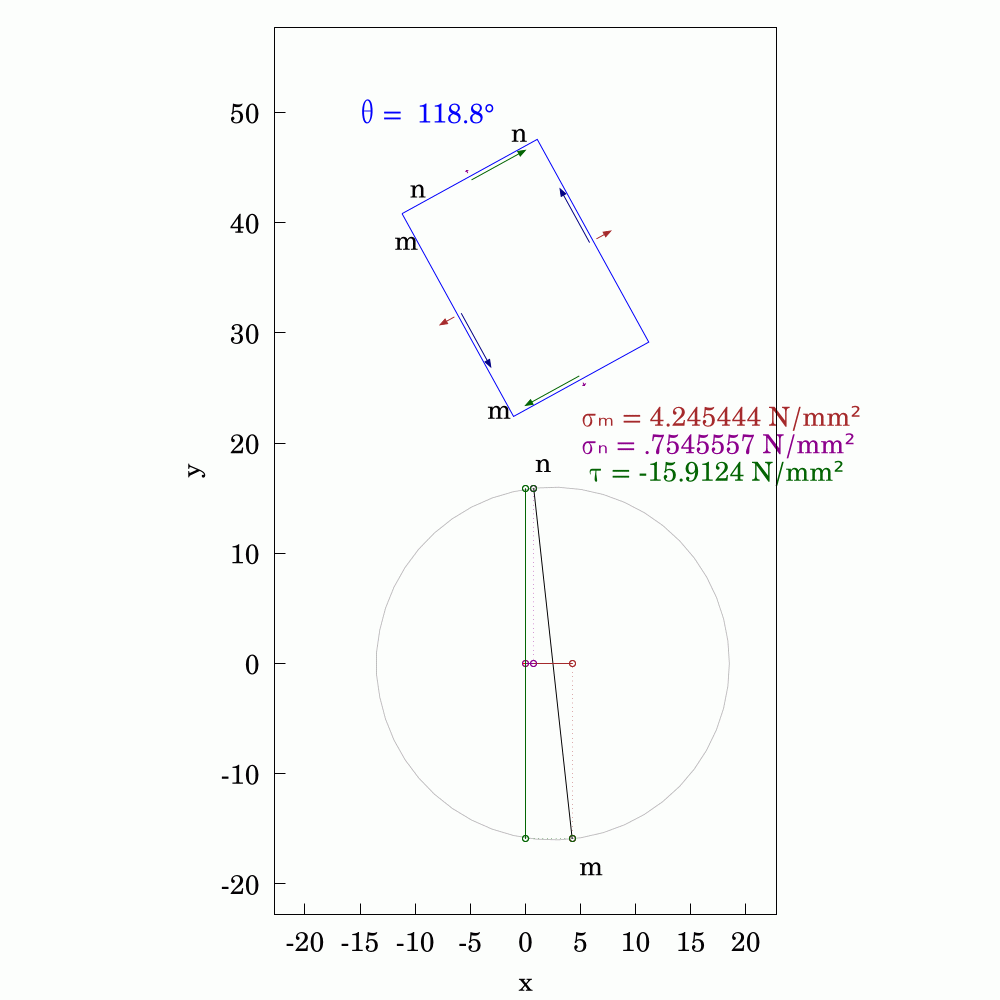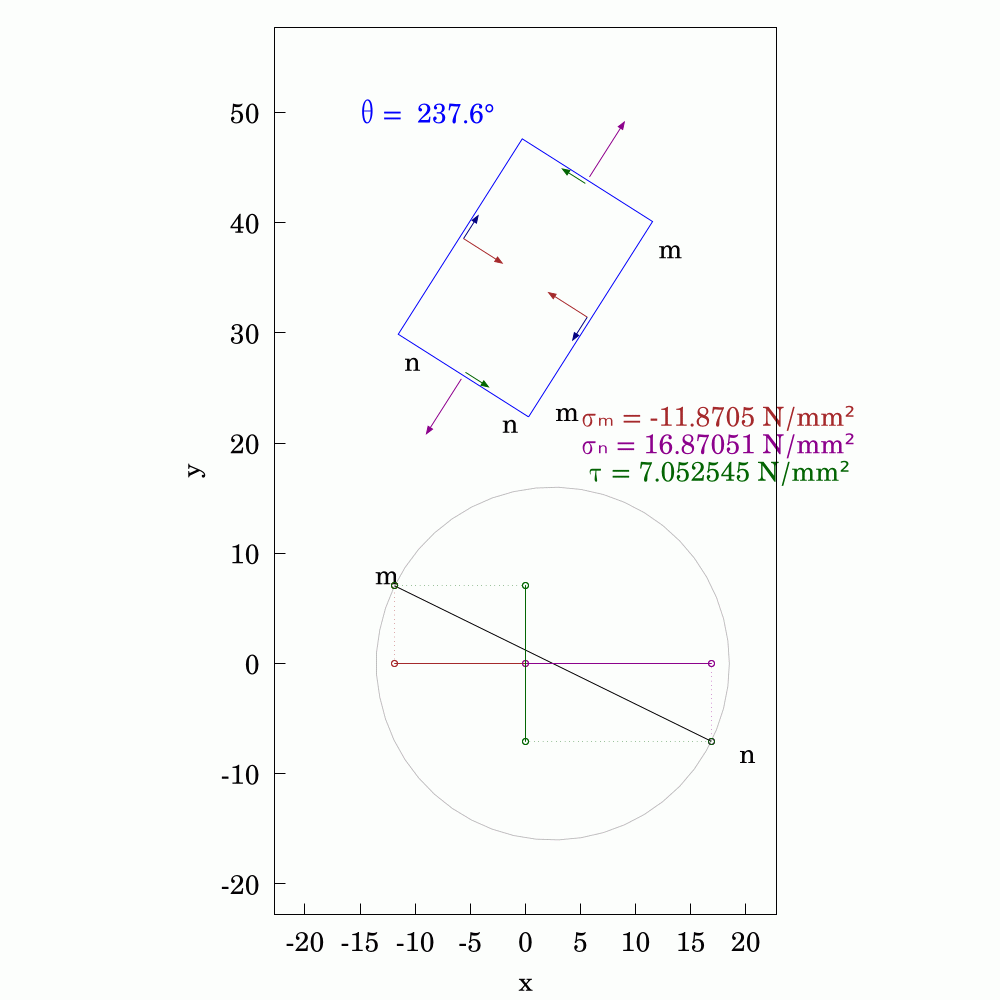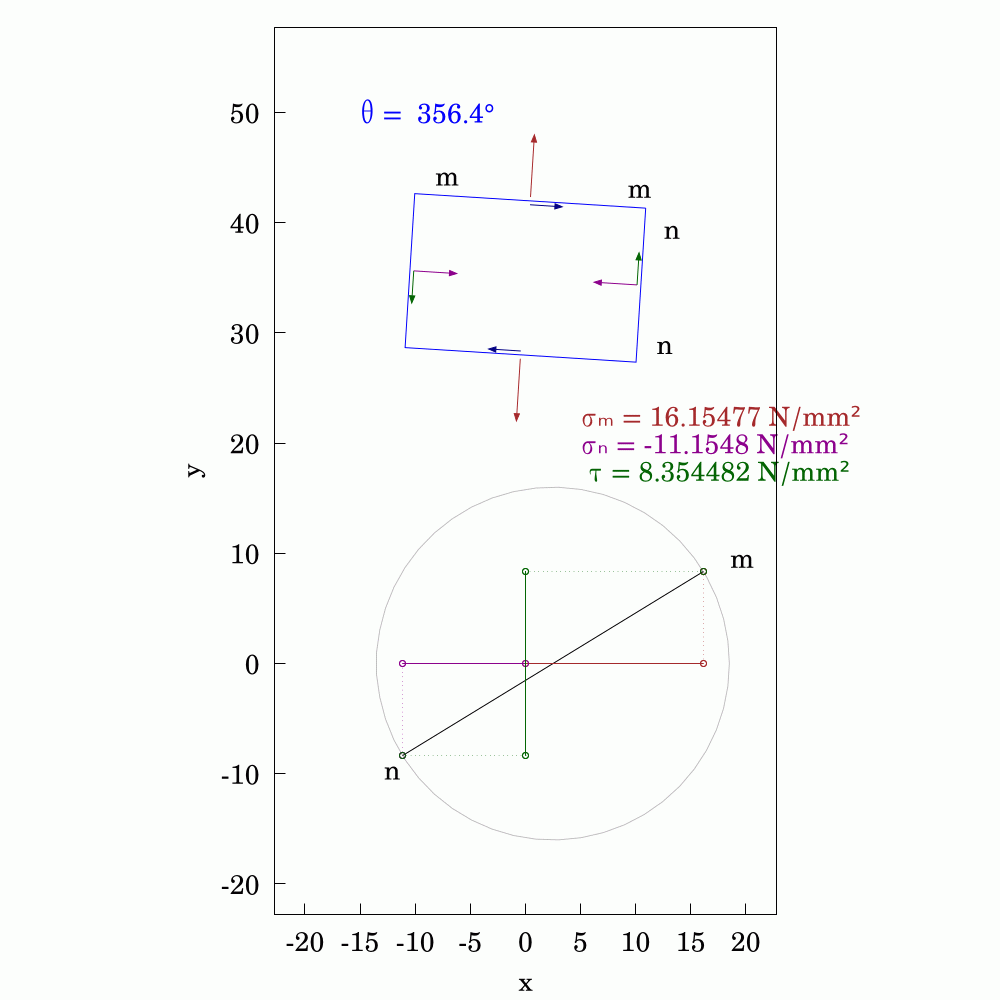
In #SolidMechanics, #stress has some counter-intuitive properties, particularly when you rotate the coordinate system. The values of normal and shear stress transform according to the rules of #second-order #tensors, which is a step above #vectors (first-order tensors). To avoid always having to use #matrix #algebra to find the components, #engineers and #mathematicians have long used the Mohr's circle to evaluate them. This is a very handy tool and allows you to find the new values by using circular geometry instead.

Here, I've used #WxMaxima to create this #animation.

#Mechanics #Mathematics #Engineering #MohrsCircle #FreeSoftware

7 Likes
14 Comments
2 Shares
opensciencedaily@diasp.org
Future Powered

Computer Scientists Prove Why Bigger Neural Networks Do Better

Our species owes a lot to opposable thumbs. But if evolution had given us extra thumbs, things probably wouldn’t have improved much. One thumb per hand is enough. Not so for neural networks, the leading artificial intelligence systems for performing humanlike tasks. As they’ve gotten bigger, they have come to grasp more. This has been a surprise to onlookers. Fundamental mathematical results had...
https://www.quantamagazine.org/computer-scientists-prove-why-bigger-neural-networks-do-better-20220210/
#science, #mathematics, #abstractions, #computer, #blog

Computer Scientists Prove Why Bigger Neural Networks Do Better | Quanta Magazine

Two researchers show that for neural networks to be able to remember better, they need far more parameters than previously thought.

opensciencedaily@diasp.org
Future Powered

Why Triangles Are Easy and Tetrahedra Are Hard

Do you think there’s a triangle whose angles measure 41, 76 and 63 degrees? At first, answering this may seem easy. From geometry class we know that the sum of the measures of the interior angles of a triangle is 180 degrees, and since 41 + 76 + 63 = 180, the answer must be yes. But there’s more to this question than meets the eye. The triangle angle sum theorem tells us that, given a triangle in...
https://www.quantamagazine.org/triangles-are-easy-tetrahedra-are-hard-20220131/
#mathematics

Why Triangles Are Easy and Tetrahedra Are Hard | Quanta Magazine

The triangle angle sum theorem makes working with triangles easy. What happens when you can’t rely on it?

4 Likes
1 Shares
6 Likes
1 Shares
2 Likes
1 Comments
opensciencedaily@diasp.org
Future Powered

The Year in Math and Computer Science

Mathematicians and computer scientists had an exciting year of breakthroughs in set theory, topology and artificial intelligence, in addition to preserving fading knowledge and revisiting old questions. They made new progress on fundamental questions in the field, celebrated connections spanning distant areas of mathematics, and saw the links between mathematics and other disciplines grow.
https://www.quantamagazine.org/the-year-in-math-and-computer-science-20211223/
#science, #computer, #mathematics

The Year in Math and Computer Science | Quanta Magazine

Mathematicians and computer scientists answered major questions in topology, set theory and even physics, even as computers continued to grow more capable.

One person like that
pratik_m@diasp.org
pratik_m

Happy #wintersolstice , and also there is another #special day #today
Today is also the #happy #birthday of #Indian #mathematician Srinivas Ramanujan, regarded as one of the greatest of Indian genii...
He was a blend of innate #talent and platonic #love towards #mathematics.
At an early age, he was taken to #Cambridge by another genius of Britain, Godfrey Harold Hardy. Together, they made several #beautiful discoveries. The #story of Ramanujan's life is indeed a wonderful piece to read, full of romance and thrills :)

One person like that
7 Comments
1 Shares
4 Likes
1 Comments
1 Shares
mkwadee@diasp.eu
Khurram Wadee

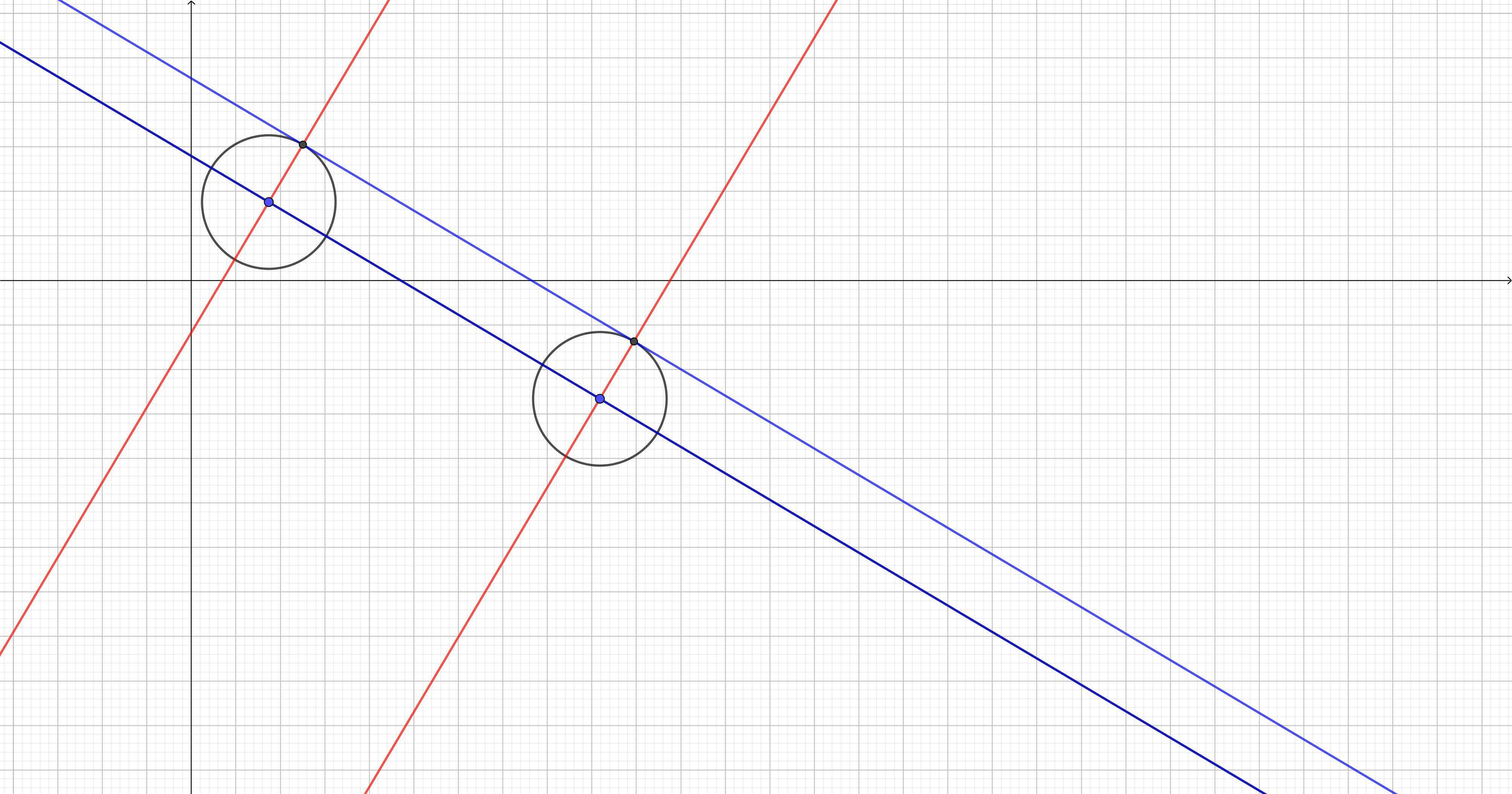
To construct a #ParallelLine to a given line (in blue) in 2D #EuclideanSpace, all you need to do is pick two #points and draw #circles centred at those points of a specified #radius. Draw a #perpendicular to the line at each point (in red) and then draw a new line passing through the intersection of the perpendicular with the circles and there is the line parallel to the original one. Here is the process shown in #Geogebra.

Parallel lines in Euclidean space

Using this #software, you can also explore #non-Euclidean space and here is the same action in #HyperbolicSpace (here in a #PoincaréDisc). #StraightLines are replaced by #GeodesicLines which look like #CircularArcs which intersect the #disc at #RightAngles. Circles are transformed to circles but their hyperbolic centres are not at the centre of their Euclidean centres. The boundary is analogous to infinity.

Repeating the construction for Euclidean space, you can see that the parallel lines diverge.

Parallel lines in hyperbolic space

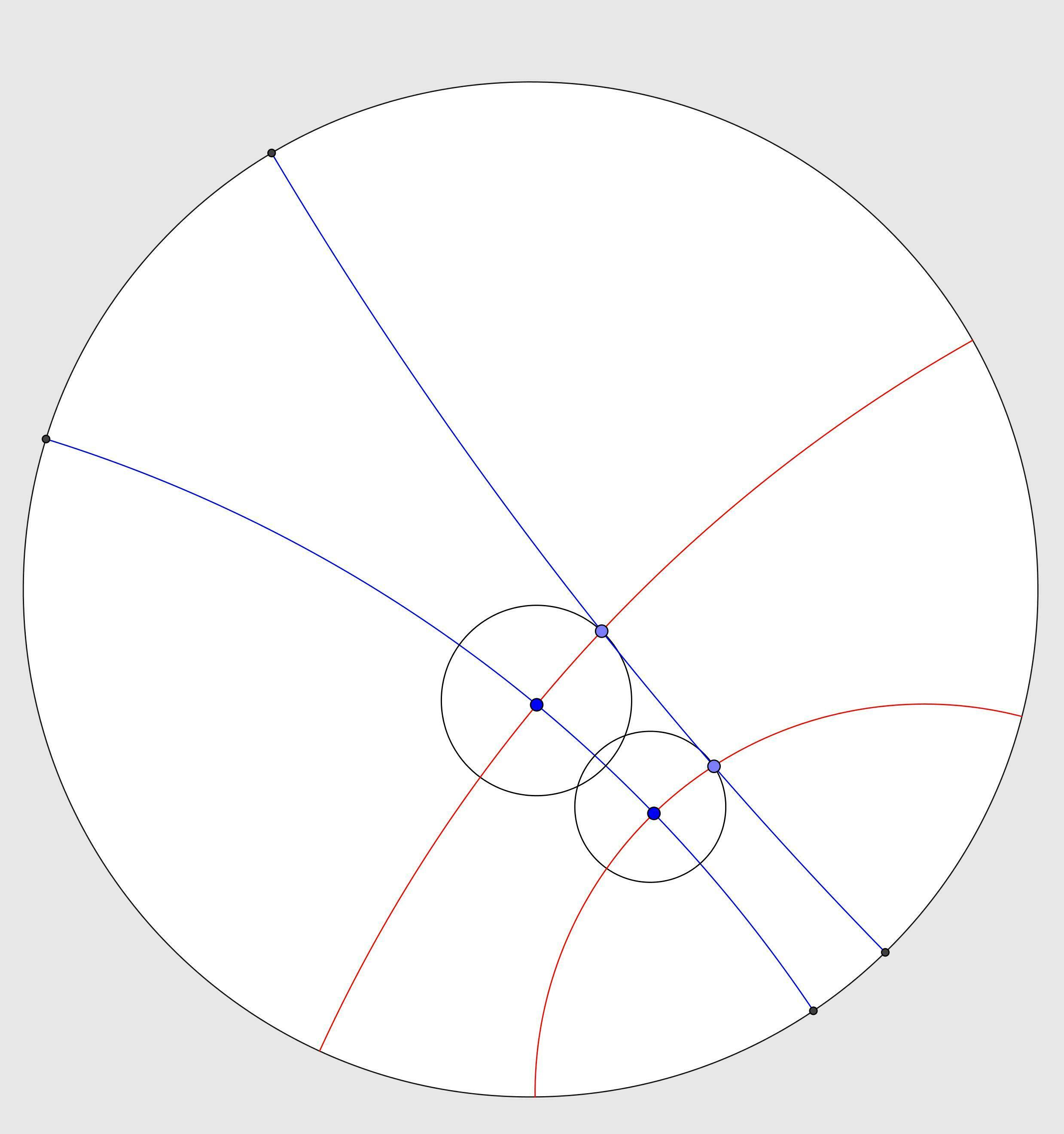
#Mathematics #Geometry #NonEucldeanGeometry #EuclideanGeometry #FreeSoftware

7 Likes
13 Comments
2 Likes