One person like that
4 Comments
1 Shares

11min : https://indymotion.fr/w/h59xdMZ6jFogpXef7WcgsN?start=1m29s
Spoiler alert : même les maths nous disent que l'égoïsme pur n'est pas une très bonne idée.
La main invisible du marché et de la concurrence ? Non, pas bon.
#Politique #Société #IntérêtGénéral #Égoïsme #Nous #Moi #Altruisme #Modélisation #Math #Libéralisme #Néolibéralisme #Capitalisme #Économie #Concurrence #LibreConcurrence #Public #Privé #MainInvisibleDuMarché #Marché
Oxford University Mathematician takes German High School Maths Exam https://youtube.com/watch?v=ZjCzWmRn6UM&feature=share
I have a beef with open source artificial intelligence the way it currently is presented.
It starts with promises. A new model like llama, much better than the predecessor due to more parameters.
Then everyone fine tunes models and uploads them.
Whenever you run into issues compiling, using and managing expectations, nobody is there to talk to, because “open source”.
Often, provided there’s documentation, it’s written for computers, not people.
Transformers being black boxes, you always have the choice to take it or leave it. There is no debugging, really.
Most, me included, do not know how the math behind it works, so we are at the mercy of tutorials, which detail an ultra-niche case, 1% of users can apply.
Is there a middle ground between pay and get support or open source, don’t complain?
#artificial-intelligence #open-source #support #debugging #documentation #math #tutorials #complaints #middle-ground #pay
Scott Galloway (marketing professor) says:
I don’t know, nobody does. However, I believe it is increasingly likely Donald Trump withdraws from the race for president as the result of a plea deal. Why? A: math.
Ya think?
Great article with some solid reasoning. Only thing is, #TrumpVirus doesn't know maths (or non-"me" logic, or stopping)
#TrumpVirus #indictment #sedition #Jan6 #treason #espionage #emoluments #math #DJT #justice #law #accountability
Numbers so large [footnote] you can barely express them and not possibly fathom them.
FTA: … the busy beaver game consists of designing a halting Turing machine with alphabet {0,1} which writes the most 1s on the tape, using only a given set of states. The rules for the 2-state game are as follows:
1 the machine must have at least two states in addition to the halting state, and
2 the tape initially contains 0s only.
A player should conceive a transition table aiming for the longest output of 1s on the tape while making sure the machine will halt eventually.
An nth busy beaver, BB-n or simply "busy beaver" is a Turing machine that wins the n-state busy beaver game. That is, it attains the largest number of 1s among all other possible n-state competing Turing machines. The BB-2 Turing machine, for instance, achieves four 1s in six steps.
Determining whether an arbitrary Turing machine is a busy beaver is undecidable. This has implications in computability theory, the halting problem, and complexity theory. The concept was first introduced by Tibor Radó in his 1962 paper, "On Non-Computable Functions". [emphasis mine. I have a particular fondness for undecidable/uncomputable functions.]
... The n-state busy beaver (BB-n) game is a contest to find such an n-state Turing machine having the largest possible score — the largest number of 1s on its tape after halting. A machine that attains the largest possible score among all n-state Turing machines is called an n-state busy beaver, and a machine whose score is merely the highest so far attained (perhaps not the largest possible) is called a champion n-state machine.
[This all sounds kinda sweet, innocent, and nerdy so far, doesn't it? But get this:]
The busy beaver function quantifies the maximum score attainable by a busy beaver on a given measure. This is a noncomputable function. Also, a busy beaver function can be shown to grow faster asymptotically than any computable function.
[Holy. Fucking. Shit. Let's say that again: ... grow faster asymptotically than any computable function. That is, in the limit, this function grows so fast that mathematics cannot even express how fast it grows. Yikes! You gotta love this. Mathematics is the best tool we have for understanding the universe. The best tool we have for understanding reality. But as Gödel famously proved, it cannot tell us all truths. [Footnote 2]]
#Math #Wonder #Complexity #BusyBeaver
Footnote: It is a mistake to refer to any integer as “large”. Let us define a number, x, as “large” if there are more numbers smaller than x than there are larger than x. For example, we can reasonably define a person, p, as “large” if there are more more people smaller than p than there are larger than p. By this criterion, I am a small person.
Consider any integer, x. If x is an integer, then x is necessarily finite. [Picture me at a kiosk with a sign reading, “Infinities are not numbers. Prove me wrong.” ;-)]
For any integer x, there is an infinity of integers larger than x, but only a finite number of integers smaller than x. (The argument becomes more complex with real numbers.) Therefore, by definition, every integer is small. QED
Footnote 2: Republicans would seize on this fact and exploit it to lie to people except that they and their base are far too fucking stupid to understand what it means.



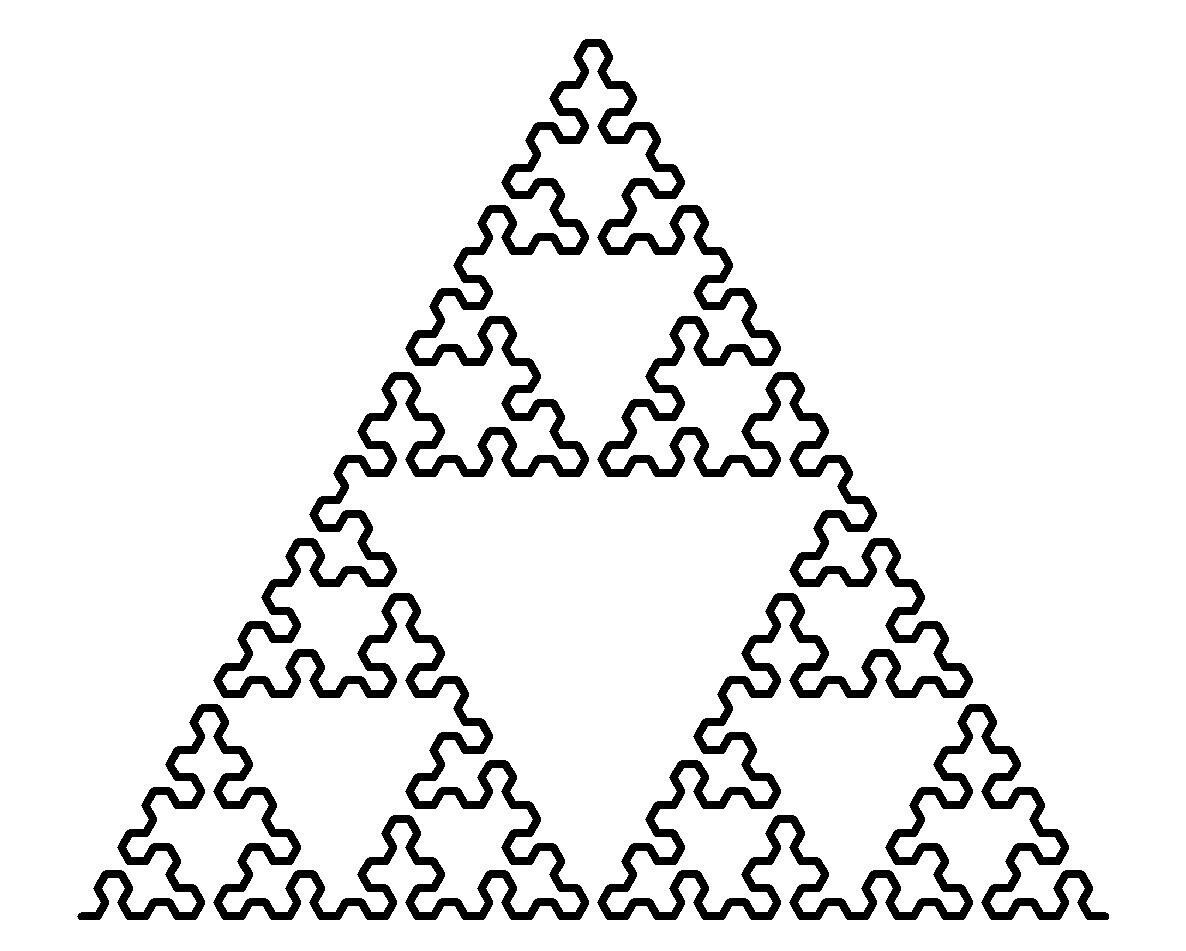
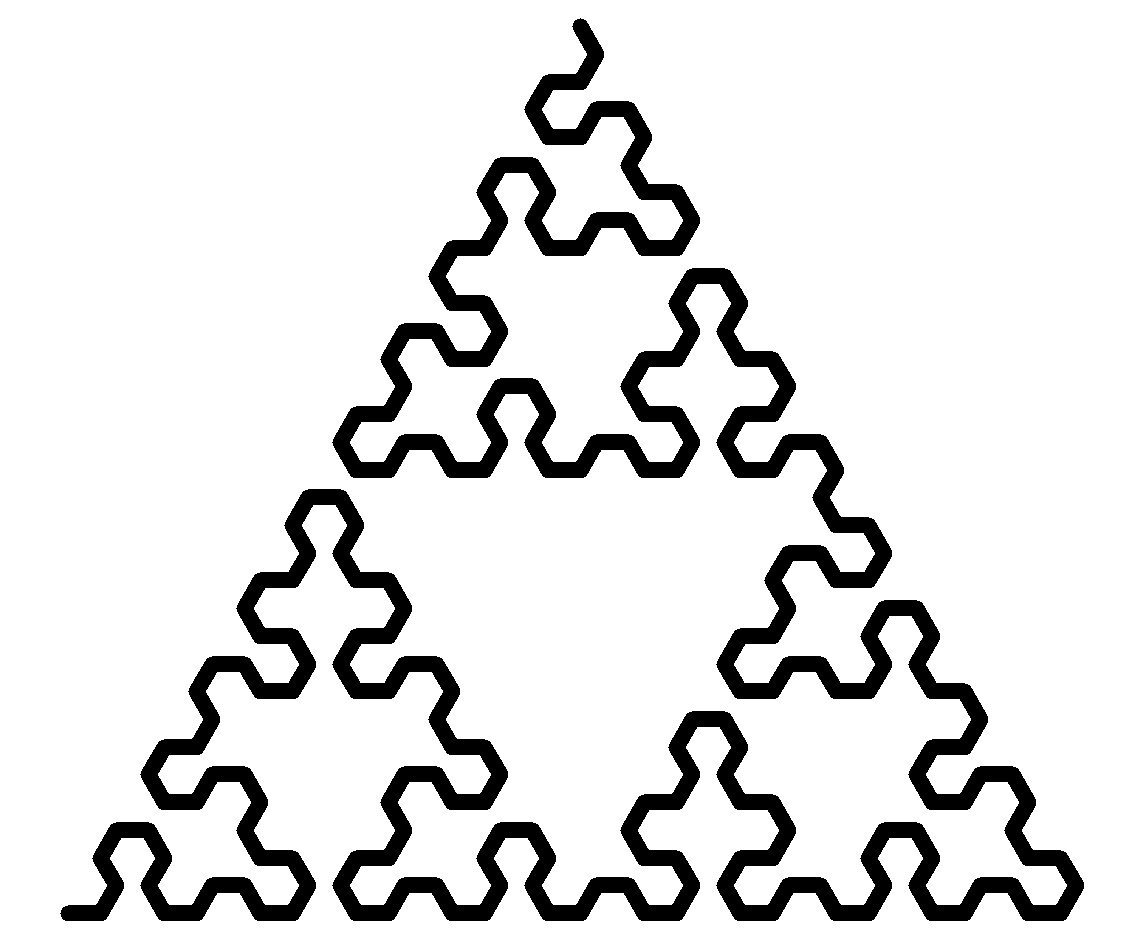
#JustForFun i created these Sierpinski triangles using #Python's #turtle module | #maths #math #programming #fractals #recursion
import logging
import turtle
import time
SPEED_INT = 5 # 1-10 where 0 is as fast as possible
logging.basicConfig(level=logging.DEBUG)
DISPLAY_WIDTH = 1620
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Sierpinski Triangle (using turtle)")
t.shape("turtle")
t.speed(SPEED_INT)
turtle.setheading(0)
# ..set start position
t.penup()
turtle.setx(-DISPLAY_WIDTH // 2)
turtle.sety(-450)
t.pendown()
start_pos = t.pos()
time.sleep(1)
def draw_recursive(i_level: int, i_direction: int):
"""Level 1 is the starting i_starting_level (0 doesn't exist)"""
logging.debug(f"{i_level * '-'} draw_recursive called with level {i_level}")
if i_level == 1:
t.forward(distance)
return
draw_recursive(i_level - 1, -i_direction)
t.left(i_direction * 60)
draw_recursive(i_level - 1, i_direction)
t.left(i_direction * 60)
draw_recursive(i_level - 1, -i_direction)
distance = 0
def draw_(i_starting_level: int, i_pen_color_channel: float = 0.0):
logging.debug(f"==== draw_ called with starting level {i_starting_level} ====")
t.penup()
t.setpos(start_pos)
t.setheading(0)
t.pendown()
global distance
distance = 1024 / (2 ** (i_starting_level - 1))
distance = min(100, distance)
pen_size = distance // 2
if pen_size < 1:
raise Exception("Pen size is smaller than one")
t.pensize(distance // 2)
t.pencolor((i_pen_color_channel,) * 3)
if i_starting_level % 2 == 0:
direction = 1
else:
direction = -1
draw_recursive(i_starting_level, direction)
# draw_(9)
pen_color_channel = 0.8
for i_starting_level in range(5, 8):
if pen_color_channel < 0:
raise Exception("Pen color channel smaller than zero")
draw_(i_starting_level, pen_color_channel)
pen_color_channel -= 0.2
t.hideturtle()
turtle.done()

#JustForFun i created these #KochSnowflake/s using #Python's #turtle module | #maths #math #programming #fractals #recursion
import logging
import turtle
import time
SPEED_INT = 4 # 1-10 where 0 is as fast as possible
logging.basicConfig(level=logging.DEBUG)
DISPLAY_WIDTH = 1620
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Koch Snowflake")
t.shape("turtle")
t.speed(SPEED_INT)
turtle.setheading(0)
# ..set start position
t.penup()
turtle.setx(-DISPLAY_WIDTH // 2)
turtle.sety(-400)
t.pendown()
start_pos = t.pos()
time.sleep(1)
def draw_recursive(i_level: int):
"""Level 1 is the starting level (0 doesn't exist)
, i_unit_distance: int
"""
if i_level == 1:
t.forward(distance)
return
draw_recursive(i_level - 1)
t.left(60)
draw_recursive(i_level - 1)
t.right(120)
draw_recursive(i_level - 1)
t.left(60)
draw_recursive(i_level - 1)
def get_distance(i_levels_to_draw):
distance_ = DISPLAY_WIDTH / (3 ** (i_levels_to_draw - 1))
return distance_
pen_color_channel = 0.9
pen_size = 16
for i in range(2, 7):
t.penup()
t.setpos(start_pos)
t.pendown()
levels_to_draw = i
distance = get_distance(levels_to_draw)
if pen_size < 1:
raise Exception("Pen size smaller than one")
t.pensize(pen_size)
pen_size = pen_size // 2
if pen_color_channel < 0:
raise Exception("Pen color channel smaller than zero")
t.pencolor((pen_color_channel,) * 3)
pen_color_channel -= 0.2
draw_recursive(levels_to_draw)
t.hideturtle()
turtle.done()




#JustForFun i created this Hilbert space-filling curve using #Python's #turtle module | #maths #math #programming
import logging
import random
import turtle
import time
SPEED_INT = 5 # 1-10 where 0 is as fast as possible
UNIT_DISTANCE = 30
logging.basicConfig(level=logging.DEBUG)
# Turtle setup
screen = turtle.getscreen()
t = turtle.getturtle()
turtle.title("Hilbert Space-filling Curve")
t.shape("turtle")
t.speed(SPEED_INT)
t.pensize(5)
t.pencolor((0, 0, 0))
t.penup()
turtle.setx(-500)
turtle.sety(-450)
t.pendown()
start_pos = t.pos()
time.sleep(1)
CW = 1
CCW = -1
def get_angle():
fuzzyness = random.choice(range(0, 2))
# degrees = 90 + fuzzyness
degrees = 90
return degrees
color_ = (0, 0, 0)
DIRECTION_UP = True
DIRECTION_DOWN = False
color_change_direction = (DIRECTION_UP, DIRECTION_UP, DIRECTION_UP)
def change_color():
global color_
global color_change_direction
index_to_change = random.choice(range(0, 3))
channel = color_[index_to_change]
if color_change_direction:
channel += 0.05
else:
channel -= 0.05
if channel > 1.0:
color_change_direction = not color_change_direction
channel = 1.0
elif channel < 0.0:
color_change_direction = not color_change_direction
channel = 0.0
new_color = turtle.pencolor()
new_color_list = list(new_color)
new_color_list[index_to_change] = channel
color_ = tuple(new_color_list)
turtle.pencolor(color_)
def draw_recursive(i_direction: int, i_level: int):
"""Level 1 is the starting level (0 doesn't exist)"""
if i_level == 1:
change_color()
def right_forward():
t.right(i_direction * get_angle())
t.forward(UNIT_DISTANCE)
def forward_right():
t.forward(UNIT_DISTANCE)
t.right(i_direction * get_angle())
if i_level > 1: draw_recursive(-i_direction, i_level - 1)
if i_level % 2 == 0:
right_forward()
else:
forward_right()
if i_level > 1: draw_recursive(i_direction, i_level - 1)
if i_level % 2 == 0:
t.right(-i_direction * get_angle())
t.forward(UNIT_DISTANCE)
t.right(-i_direction * get_angle())
else:
t.forward(UNIT_DISTANCE)
if i_level > 1: draw_recursive(i_direction, i_level - 1)
if i_level % 2 == 0:
forward_right()
else:
right_forward()
if i_level > 1: draw_recursive(-i_direction, i_level - 1)
turtle.setheading(90)
draw_recursive(CW, 5)
t.hideturtle()
turtle.done()
Does Math improve brain function?
Is exercising math good for the brain?
Yes, because you gain a greater ability to solve problems and stay focused.
The brain exercise that you practice today leads to a decrease in the deterioration of cognitive functions that occurs over time and with it the probability of suffering from Alzheimer’s. The benefits obtained in the improvement of your cerebral capacity are maintained through time. Your life is easier. You’ll have fewer difficulties in your daily tasks.
#Hola a todos, soy Juan Manuel, de Colombia, Sudamérica. Soy Ingeniero Civil pero la mayor parte de mi vida profesional la he dedicado a la docencia.
Soy cristiano, muy cercano a la #teologíareformada y el #calvinismo.
Tengo interés en #Jesus, #Jesús, #christian, #God, #reformedtheology, #teología, #theology, #highschool, #juniorhighschool, #matemática, #math, #middleschool, #teaching, #movilidadsostenible, #sustainablemobility, #Husqvarna, #KTM, #RoyalEnfield, #motorbike, #motorcycle, #motos, #GasGas, #barba, #beards, #cats, #dogs
#Hello everyone, I'm Juan Manuel, from Colombia, South America. I'm a Civil Engineer but most of my professional life has been dedicated to teaching.
I'm a Christian, very close to #reformedtheology and #calvinism.
#Bonjour à tous, je m'appelle Juan Manuel et je viens de Colombie, en Amérique du Sud. Je suis ingénieur civil, mais la majeure partie de ma vie professionnelle a été consacrée à l'enseignement.
Je suis chrétien, très proche de la #théologieréformée et du #calvinisme.

For whatever reason, RPN didn’t really succeed in the general marketplace, and you might wonder why it was ever a thing. The biggest reason is that RPN is very easy to implement compared to working through proper algebraic, or infix, notation. In addition, in the early years of computers and calculators, you didn’t have much to work with, and people were used to using slide rules, so having something that didn’t take a lot of code that matched how users worked anyway was a win-win.
With RPN, there is no ambiguity depending on secret rules or parentheses, nor is there any reason to remember things unnecessarily. Processing RPN, on the other hand, is easy. If you see a number, push it on the value stack. If you see an operator, pop off enough stuff from the stack, do the operation, and put the result back on the stack.
See https://hackaday.com/2023/06/21/in-praise-of-rpn-with-python-or-c/
#Blog, #math, #python, #RPN, #technology
Fermat's Library on Twitter: "If you put a spherical loaf of bread through a bread slicer, then each slice comes out with equal crust https://t.co/Zz0mGJVF02" / Twitter
https://nitter.net/fermatslibrary/status/1665326136702771200
https://twitter.com/fermatslibrary/status/1665326136702771200
If you put a spherical loaf of bread through a bread slicer, then each slice comes out with equal crust pic.twitter.com/Zz0mGJVF02
— Fermat's Library (@fermatslibrary) June 4, 2023
Learning to count

https://va.media.tumblr.com/tumblr_rv9w2g1Xq51qa1gsx.mp4
19 sec video w/sound
#video #count #math #lol