#math
Mathematical recreation
Why do prime numbers make these spirals?
I came across this video some weeks ago, perhaps right here on Pluspora (if so, I apologize for failing to credit the person who first posted it).
If you have any interest in number theory, this video is a jewel.
If you have no interest in number theory, this video will show you the error of your ways ;-)
It is at once fascinating and completely understandable, and it clears up a mystery which turns out to be no mystery at all. (Such is the way with pure math: Everything is the way it is because logically it simply could not be any other way. And when you discover why it must be as it is, it is deliciously, orgasmically obvious.)
#Math #PureMath #NumberTheory #PrimeNumbers #Integers #RealNumbers #IntegersVsReals
LibreOffice new guides ##
Brand new #LibreOffice #Calc and #Math #guides from TDF website: https://documentation.libreoffice.org/assets/Uploads/Documentation/en/CG7.0/CG70-CalcGuide.pdf
https://documentation.libreoffice.org/assets/Uploads/Documentation/en/MG7.0/MG70-MathGuide.pdf
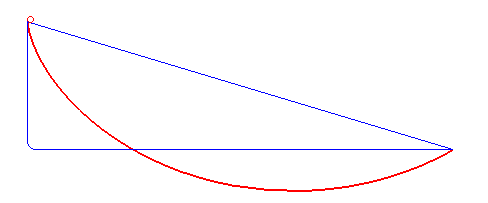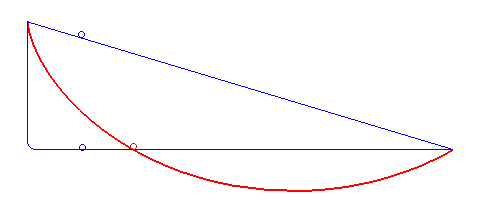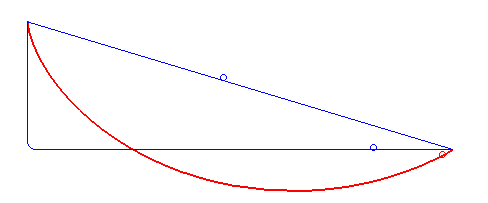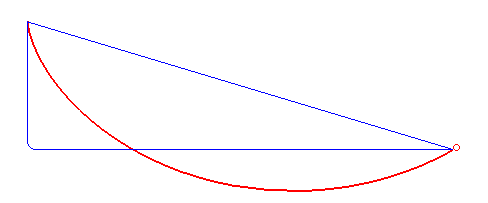
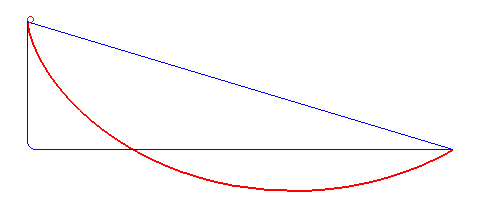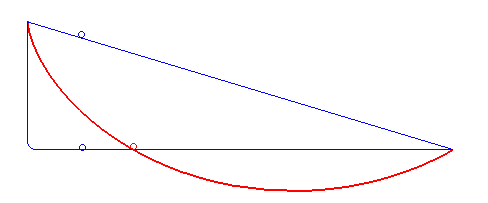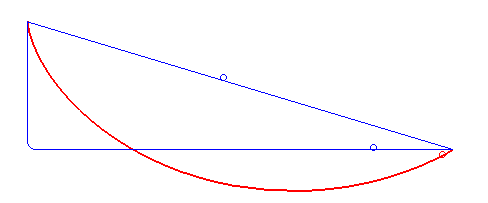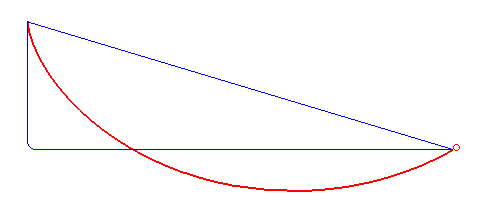
A #brachistochrone #curve is the curve of fastest descent between two points not directly below each other -- interestingly not a straight or polygonal line but a cycloid.
An #Amoeba Based #Computer #Calculated #Approximate #Solutions to a Very #Hard #Math #Problem
These single-celled organisms have a strange computing capacity that allows them to generate approximate solutions to a computationally complex problem known as the “traveling salesman problem.”
https://motherboard.vice.com/en_us/article/gy7994/an-amoeba-based-computer-calculated-approximate-solutions-to-a-very-hard-math-problem
Hey everyone, I’m #newhere, a refugee from Google+. I’m interested in #education, #environment, #humor, #math, #politcs, and #science.
Bon et donc c'est cool j'ai implémenté côté GPU une génération de diagrammes de Vonoroï en deux variantes convoluées avec une cloche générée avec la formule d'interpolation utilisée dans le bruit de Perlin amélioré. C'est d'ailleurs cette cloche qui remplacera, en plus des autres tampons le cône que j'utilisais dans le stamp noise.
Comme le procédé est très simple à expliquer je devrais sortir un article très bientôt sur le sujet :)
À bientôt!
#Perlin #BruitDePerlin #GénérationProcédurale #Procédurale #Algorithme #OpenSource #Libre #CC #CreativeCommon #Blog #UNIVERSE #denissalem #OpenGL #VR #RéalitéVirtuel #univers #3D #math #algorithmique #analyse #mathématique #mathématiques #GNU-GPL #dev #devlog #log #developpement #logiciel #geek #free #StampNoise #CoherentNoise #simulation #Art #code #coding #generativeArt #generativeDesign #generative #science #fractal #fractalArt #GPL #technologie #GPU #Graphic #Render #Rendering #Graphique #PoC #ProofOfConcept #Shader #ComputeShader
The question is not even "How do #mathematicians make progress in #mathematics?" Rather, as a more explicit (and leading) form of the question, I prefer "How do mathematicians advance human understanding of mathematics?"
This question brings to the fore something that is fundamental and pervasive:that what we are doing is finding ways for people to understand and think about mathematics. The rapid advance of computers has helped dramatize this point, because computers and people are very different. For instance, when Appel and Haken completed a proof of the 4-color map theorem using a massive automatic computation, it evoked much controversy. I interpret the controversy as having little to do with doubt people had as to the veracity of the theorem or the correctness of the proof. Rather, it reflected a continuing desire for human understanding of a proof, in addition to knowledge that the theorem is true. On a more everyday level, it is common for people first starting to grapple with computers to make large-scale computations of things they might have done on a smaller scale by hand. They might print out a table of the first10,000 primes, only to find that their printout isn’t something they really wanted after all. They discover by this kind of experience that what they really want is usually not some collection of “answers”—what they want is understanding․
As a mathematician, I always feel alienated, because of how little people know about maths, and because every non mathematician just scares when you start explaining something, even the easiest thing. “Oh, please, stop. Anyway I won’t get a thing”. This is the regular reaction of people.
Most people don’t know what #math is. But the worst part is, that they not only don’t know, they don’t want to know. Math scares them. Even physics doesn’t scare them as much, as math. Maybe because there is something that can be shown. (And also due to the great books of Stephan #Hawking and Carl #Sagan) But when it comes to Mathematics, everything becomes more complicated, because you can’t show it. It’s too abstract. And, it even doesn’t really exist. :)
So, I don’t have to say how much I appreciate when I see a popular #book about #maths. For me, as a reader, Edward #Frenkel's book “Love and Math” was a great read. (especially the beginning of the book, last chapter or two were bullshit…ehm, sorry). He showed how much Math mattered. He showed that it’s not a tool for #physics, but it can be the one which directs it.
Today I wanted to write about other book, a comic book about #logic “Logicomix”. When I started writing this post, I realized that what I want to say and how I feel about this book, is not quite about the book. This book. It’s more about my view of math, and how it should be represented to non mathematicians. And my concerns about this book are not relevant. They have done what they thought was important, telling all these stories about #Russell and war, and not paying that much attention to #Gödel, #Turing and Von Neumann. (Actually there was too little math in it. But I was very impressed when they wrote about #Frege (without explaining his system, without pointing out differences between Frege’s and #Aristotle's systems)).
Now I’m considering writing small blog posts on math for non mathematicians :)
