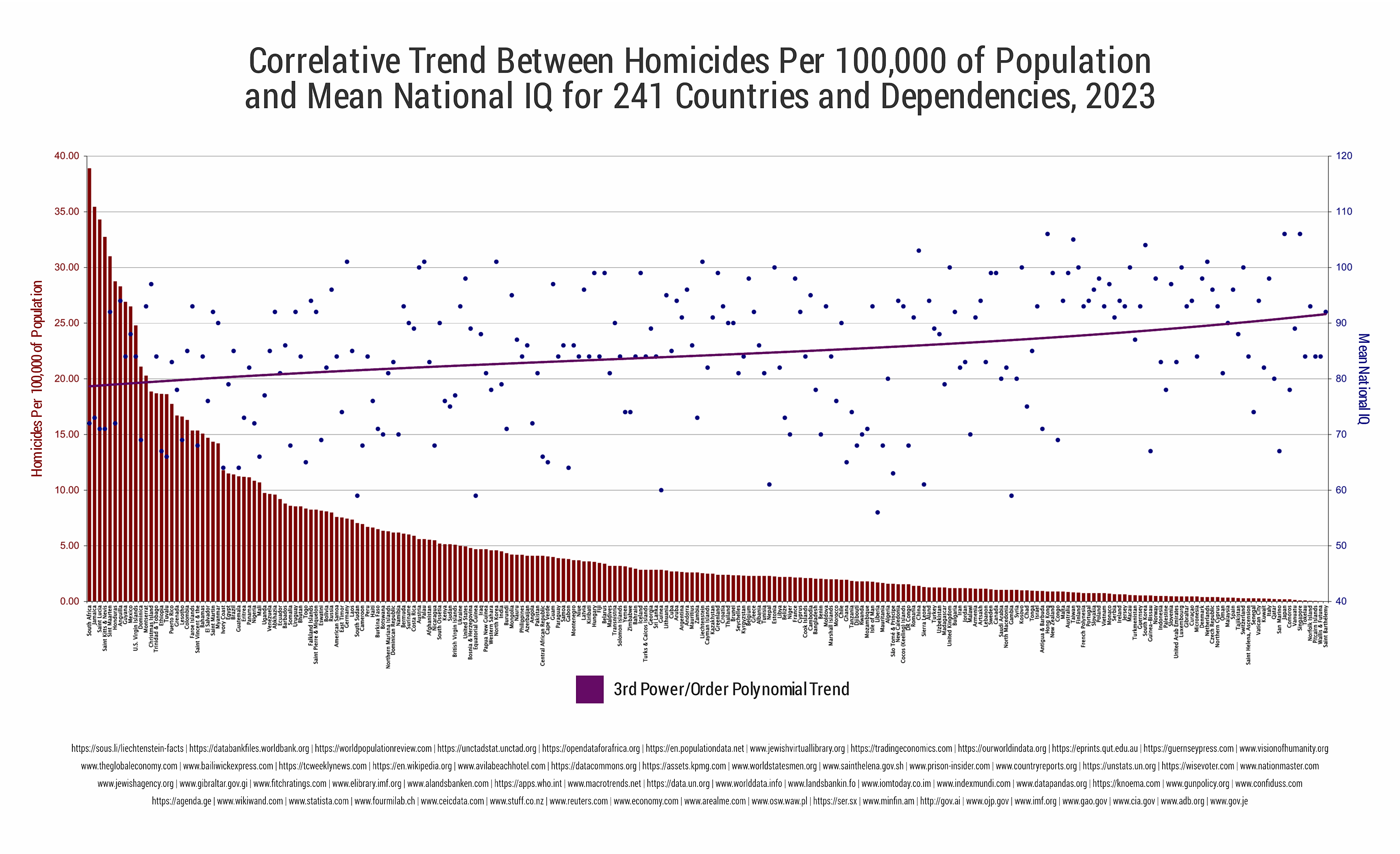
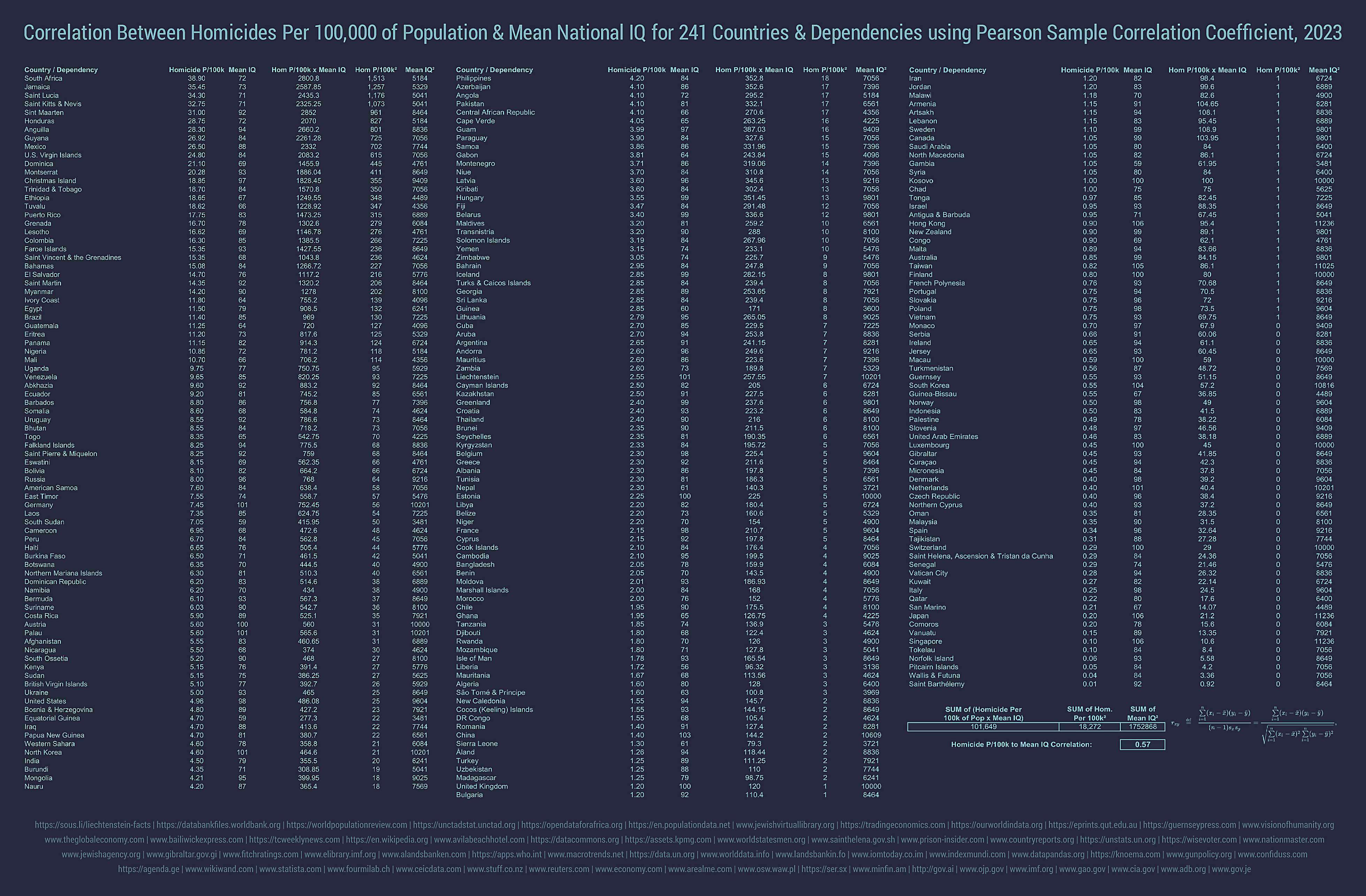
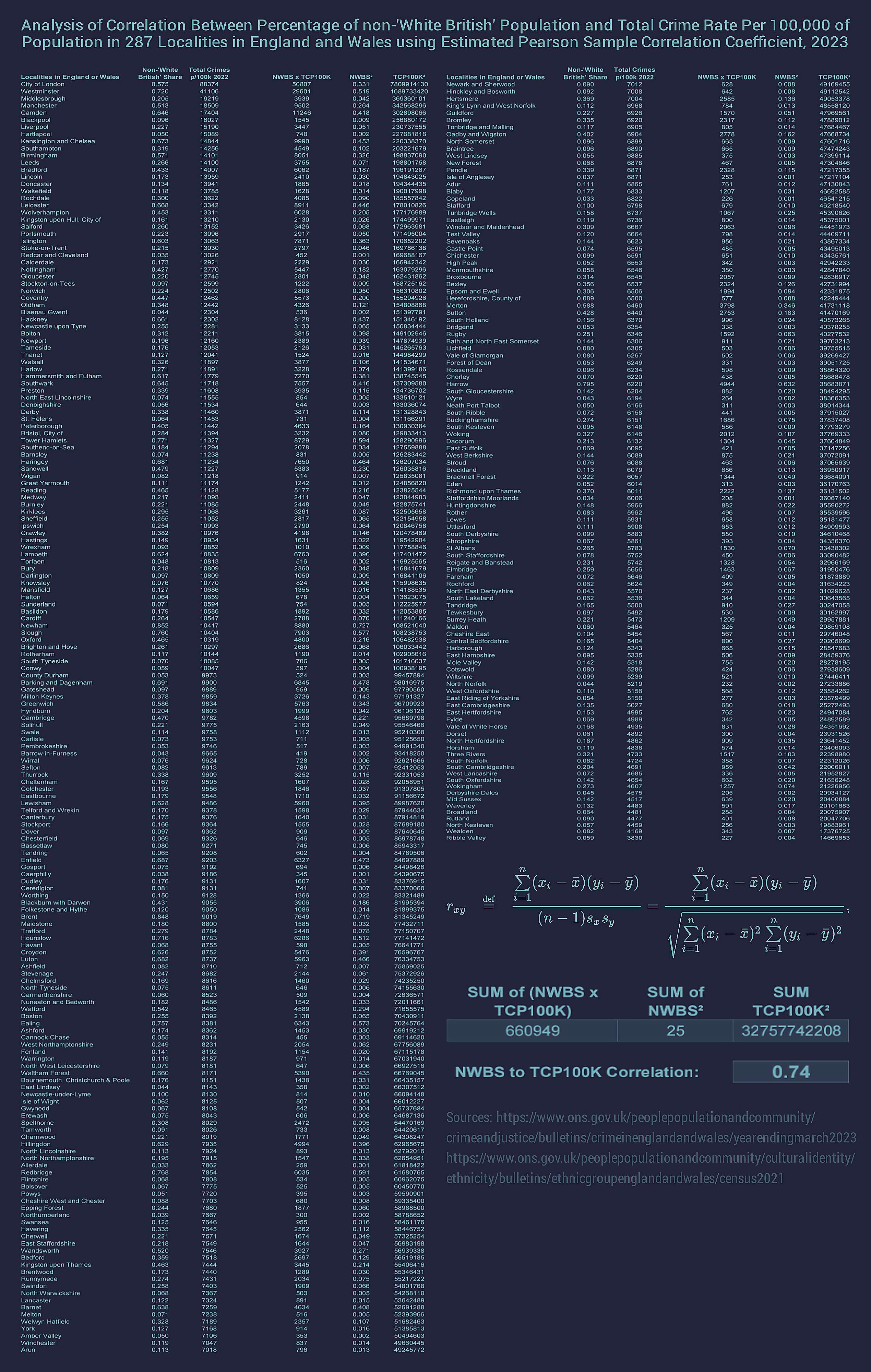
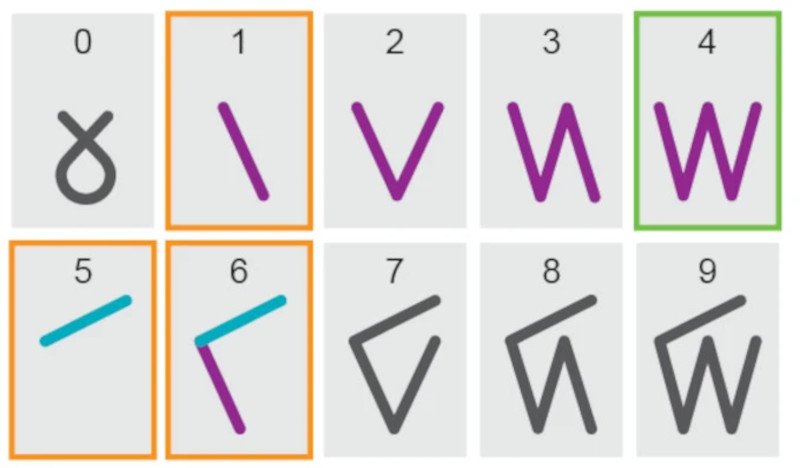
"An aperiodic monotile exists!" And is being reported on a website called "The Aperiodical". A website created before the discovery of the aperiodic monotile. (Made by Katie Steckles, who I know from YouTube, and two friends of hers).
"The tile is made of eight kites -- the shape you get by cutting a hexagon up through the midpoints of its edges." "There's a whole continuous family of aperiodic monotiles, obtained by changing the lengths of the edges in the shape."
Aperiodic means it doesn't repeat periodically. It forms a pattern that is infinite yet non-repeating.
Actually this shape isn't the only shape that can form aperiodic tiling. It's the first that can form only aperiodic tiling. There's a "pinwheel" tiling based on a triangle of a specific shape. But that shape can also make periodic tilings. The "hat" shape her can only make aperiodic tilings.
The proof was done by computer to check every edge case and there's a website you can use to create your own (finite) tilings. The proof involves creating four "clusters" that are groupings of "hats" and proving that the four clusters form larger groups called metatiles, which have the same symmetries as the basic tiles. This makes it possible to prove there's no translational symmetry at any scale.
This news isn't exactly going to transform the whole world, except for people who care whether their kitchen's tiling is periodic or aperiodic.
#mathematics #monotiles
https://aperiodical.com/2023/03/an-aperiodic-monotile-exists/